Question Number 181426 by universe last updated on 25/Nov/22

Commented by universe last updated on 25/Nov/22

$${true}\:{or}\:{false}\:? \\ $$
Answered by mr W last updated on 25/Nov/22
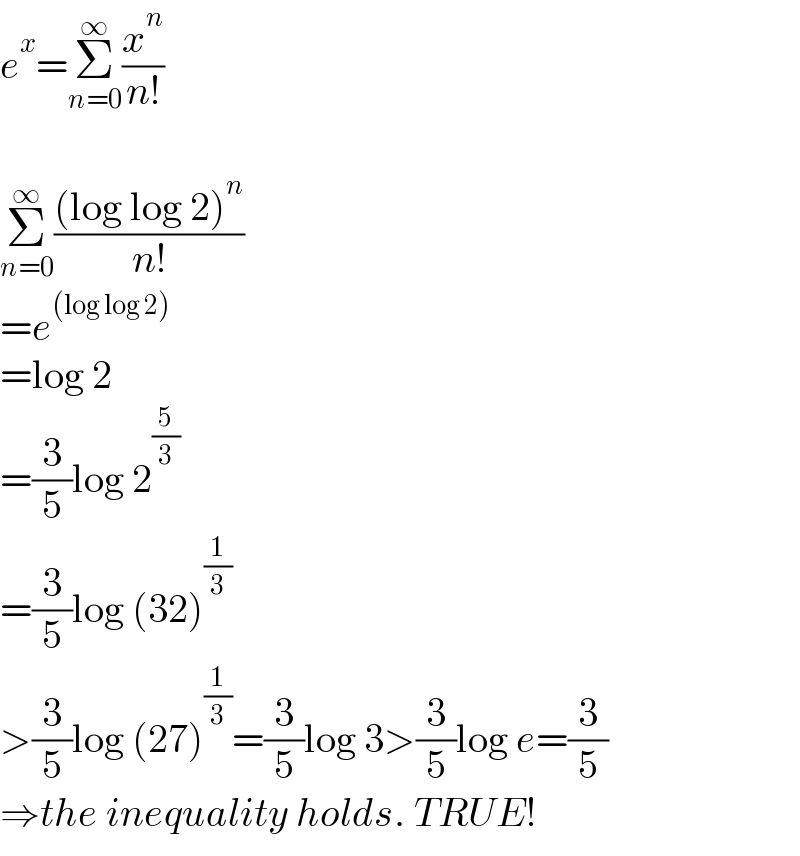
$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$$ \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{log}\:\mathrm{log}\:\mathrm{2}\right)^{{n}} }{{n}!} \\ $$$$={e}^{\left(\mathrm{log}\:\mathrm{log}\:\mathrm{2}\right)} \\ $$$$=\mathrm{log}\:\mathrm{2} \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}}\mathrm{log}\:\mathrm{2}^{\frac{\mathrm{5}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}}\mathrm{log}\:\left(\mathrm{32}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$>\frac{\mathrm{3}}{\mathrm{5}}\mathrm{log}\:\left(\mathrm{27}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\frac{\mathrm{3}}{\mathrm{5}}\mathrm{log}\:\mathrm{3}>\frac{\mathrm{3}}{\mathrm{5}}\mathrm{log}\:{e}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow{the}\:{inequality}\:{holds}.\:{TRUE}! \\ $$
Commented by universe last updated on 25/Nov/22

$${thank}\:{sir} \\ $$
