Question-181432

Facebook Tweet Pin

Question Number 181432 by mr W last updated on 25/Nov/22

Commented by mr W last updated on 25/Nov/22

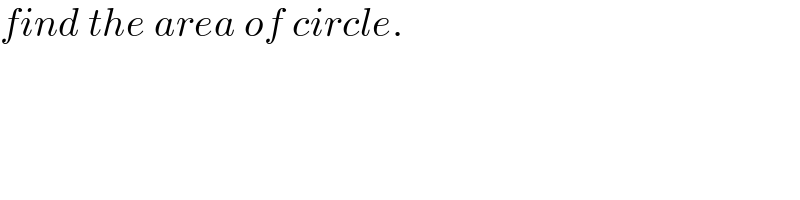
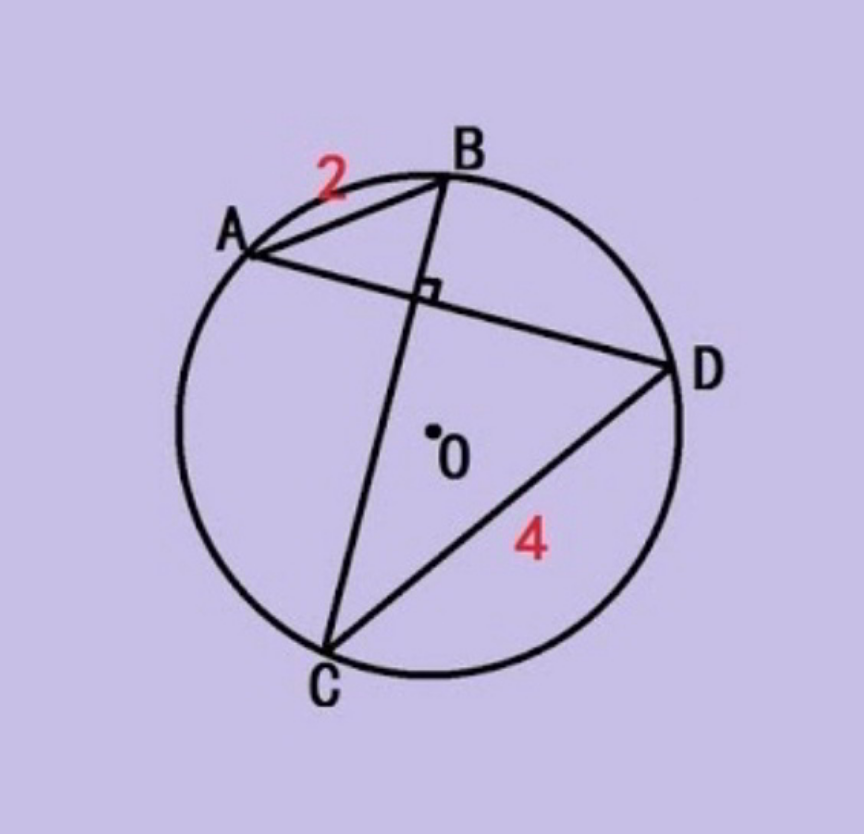
$${find}\:{the}\:{area}\:{of}\:{circle}. \\ $$

Commented by universe last updated on 25/Nov/22

Commented by universe last updated on 25/Nov/22

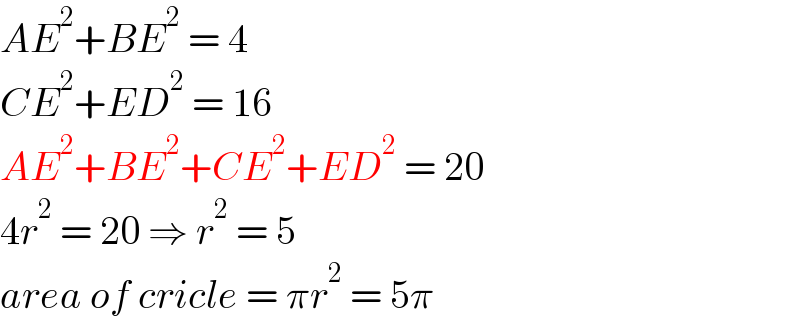
AE^2 +BE^2 = 4 CE^2 +ED^2 = 16 AE^2 +BE^2 +CE^2 +ED^2 = 20 4r^2 = 20 ⇒ r^2 = 5 area of cricle = πr^2 = 5π

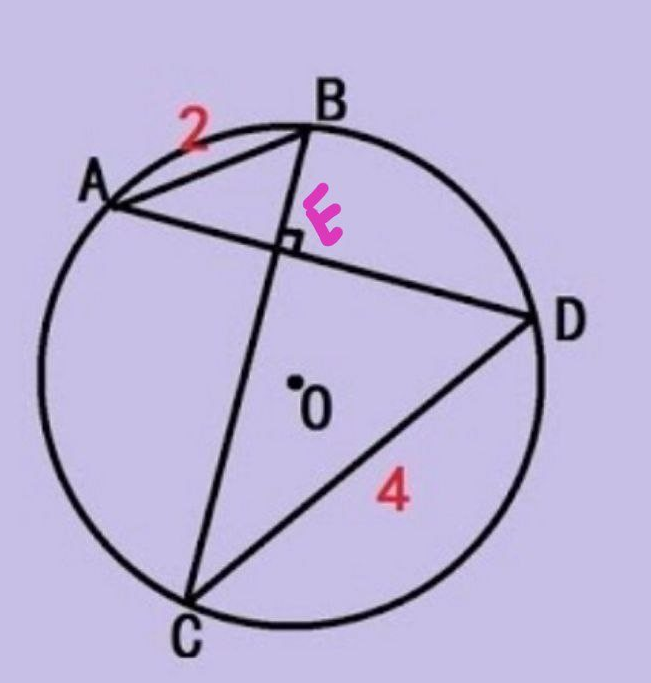
$${AE}^{\mathrm{2}} +{BE}^{\mathrm{2}} \:=\:\mathrm{4} \\ $$$${CE}^{\mathrm{2}} +{ED}^{\mathrm{2}} \:=\:\mathrm{16} \\ $$$${AE}^{\mathrm{2}} +{BE}^{\mathrm{2}} +{CE}^{\mathrm{2}} +{ED}^{\mathrm{2}} \:=\:\mathrm{20} \\ $$$$\mathrm{4}{r}^{\mathrm{2}} \:=\:\mathrm{20}\:\Rightarrow\:{r}^{\mathrm{2}} \:=\:\mathrm{5} \\ $$$${area}\:{of}\:{cricle}\:=\:\pi{r}^{\mathrm{2}} \:=\:\mathrm{5}\pi \\ $$

Commented by mr W last updated on 25/Nov/22

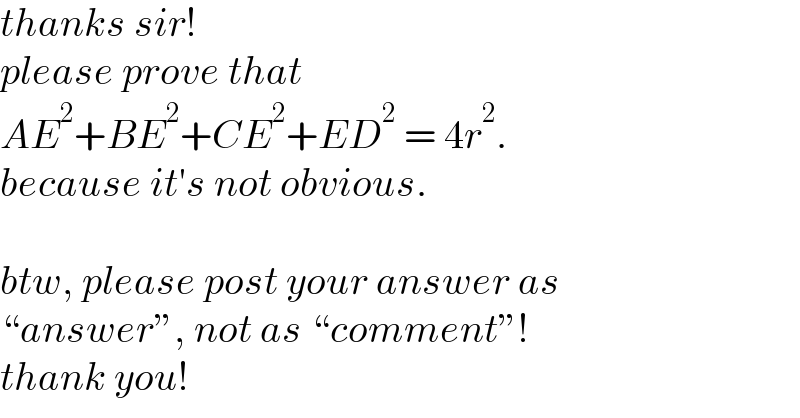
thanks sir! please prove that AE^2 +BE^2 +CE^2 +ED^2 = 4r^2 . because it′s not obvious. btw, please post your answer as “answer”, not as “comment”! thank you!

$${thanks}\:{sir}! \\ $$$${please}\:{prove}\:{that} \\ $$$${AE}^{\mathrm{2}} +{BE}^{\mathrm{2}} +{CE}^{\mathrm{2}} +{ED}^{\mathrm{2}} \:=\:\mathrm{4}{r}^{\mathrm{2}} . \\ $$$${because}\:{it}'{s}\:{not}\:{obvious}. \\ $$$$ \\ $$$${btw},\:{please}\:{post}\:{your}\:{answer}\:{as} \\ $$$$“{answer}'',\:{not}\:{as}\:“{comment}''! \\ $$$${thank}\:{you}! \\ $$

Commented by universe last updated on 25/Nov/22

https://youtu.be/1EkoaQJyrfk

Answered by HeferH last updated on 25/Nov/22

Commented by HeferH last updated on 25/Nov/22

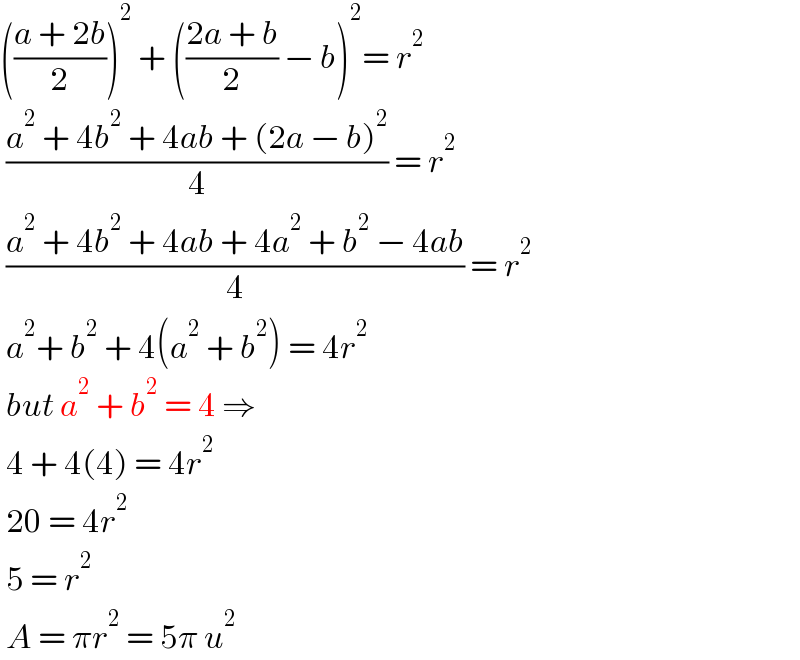
(((a + 2b)/2))^2 + (((2a + b)/2) − b)^2 = r^2 ((a^2 + 4b^2 + 4ab + (2a − b)^2 )/4) = r^2 ((a^2 + 4b^2 + 4ab + 4a^2 + b^2 − 4ab)/4) = r^2 a^2 + b^2 + 4(a^2 + b^2 ) = 4r^2 but a^2 + b^2 = 4 ⇒ 4 + 4(4) = 4r^2 20 = 4r^2 5 = r^2 A = πr^2 = 5π u^2

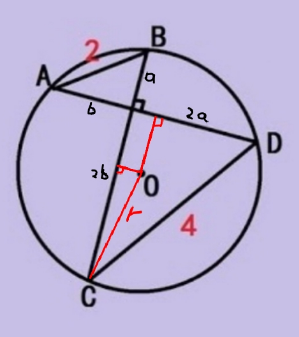
$$\left(\frac{{a}\:+\:\mathrm{2}{b}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\:\left(\frac{\mathrm{2}{a}\:+\:{b}}{\mathrm{2}}\:−\:{b}\right)^{\mathrm{2}} =\:{r}^{\mathrm{2}} \\ $$$$\:\frac{{a}^{\mathrm{2}} \:+\:\mathrm{4}{b}^{\mathrm{2}} \:+\:\mathrm{4}{ab}\:+\:\left(\mathrm{2}{a}\:−\:{b}\right)^{\mathrm{2}} }{\mathrm{4}}\:=\:{r}^{\mathrm{2}} \:\: \\ $$$$\:\frac{{a}^{\mathrm{2}} \:+\:\mathrm{4}{b}^{\mathrm{2}} \:+\:\mathrm{4}{ab}\:+\:\mathrm{4}{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:−\:\mathrm{4}{ab}}{\mathrm{4}}\:=\:{r}^{\mathrm{2}} \\ $$$$\:{a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \:+\:\mathrm{4}\left({a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \right)\:=\:\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\:{but}\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:=\:\mathrm{4}\:\Rightarrow \\ $$$$\:\mathrm{4}\:+\:\mathrm{4}\left(\mathrm{4}\right)\:=\:\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\:\mathrm{20}\:=\:\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\:\mathrm{5}\:=\:{r}^{\mathrm{2}} \\ $$$$\:{A}\:=\:\pi{r}^{\mathrm{2}} \:=\:\mathrm{5}\pi\:{u}^{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply