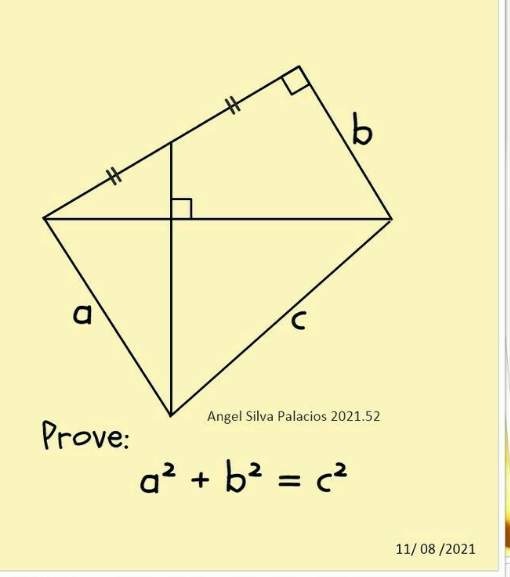
Question Number 181437 by mnjuly1970 last updated on 25/Nov/22
Answered by MJS_new last updated on 25/Nov/22
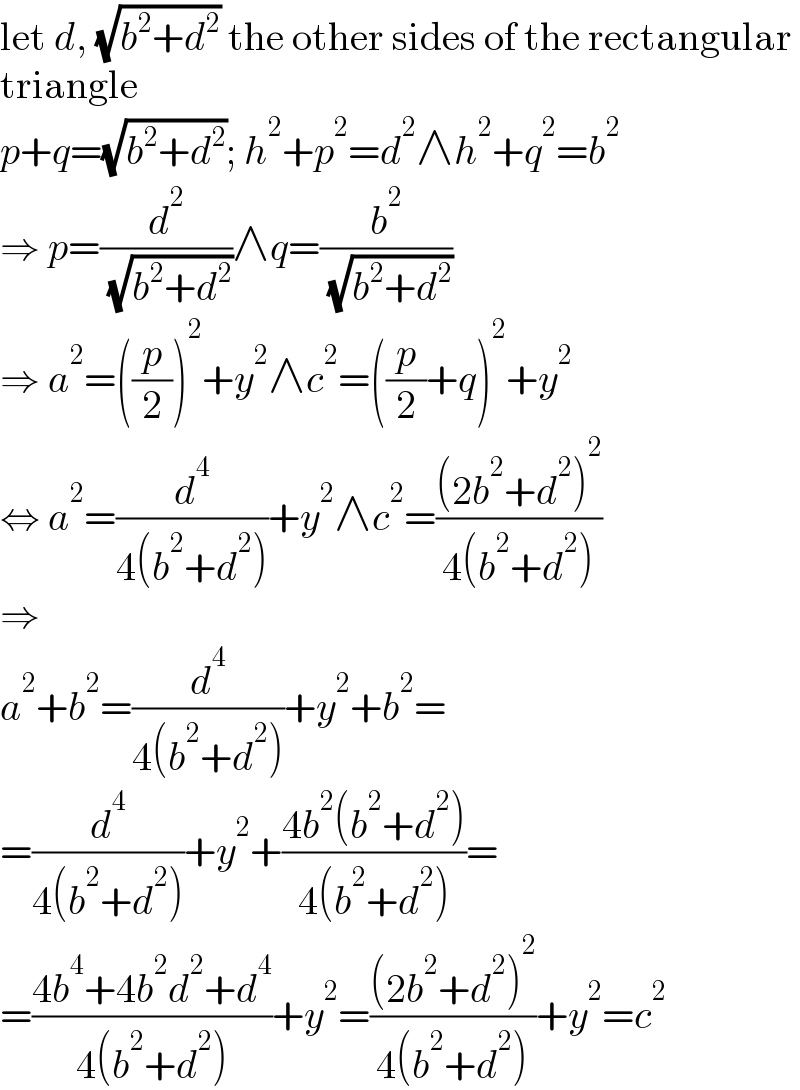
$$\mathrm{let}\:{d},\:\sqrt{{b}^{\mathrm{2}} +{d}^{\mathrm{2}} }\:\mathrm{the}\:\mathrm{other}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rectangular} \\ $$$$\mathrm{triangle} \\ $$$${p}+{q}=\sqrt{{b}^{\mathrm{2}} +{d}^{\mathrm{2}} };\:{h}^{\mathrm{2}} +{p}^{\mathrm{2}} ={d}^{\mathrm{2}} \wedge{h}^{\mathrm{2}} +{q}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\Rightarrow\:{p}=\frac{{d}^{\mathrm{2}} }{\:\sqrt{{b}^{\mathrm{2}} +{d}^{\mathrm{2}} }}\wedge{q}=\frac{{b}^{\mathrm{2}} }{\:\sqrt{{b}^{\mathrm{2}} +{d}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} =\left(\frac{{p}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \wedge{c}^{\mathrm{2}} =\left(\frac{{p}}{\mathrm{2}}+{q}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\Leftrightarrow\:{a}^{\mathrm{2}} =\frac{{d}^{\mathrm{4}} }{\mathrm{4}\left({b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}+{y}^{\mathrm{2}} \wedge{c}^{\mathrm{2}} =\frac{\left(\mathrm{2}{b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}\left({b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{{d}^{\mathrm{4}} }{\mathrm{4}\left({b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}+{y}^{\mathrm{2}} +{b}^{\mathrm{2}} = \\ $$$$=\frac{{d}^{\mathrm{4}} }{\mathrm{4}\left({b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}+{y}^{\mathrm{2}} +\frac{\mathrm{4}{b}^{\mathrm{2}} \left({b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}{\mathrm{4}\left({b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}= \\ $$$$=\frac{\mathrm{4}{b}^{\mathrm{4}} +\mathrm{4}{b}^{\mathrm{2}} {d}^{\mathrm{2}} +{d}^{\mathrm{4}} }{\mathrm{4}\left({b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}+{y}^{\mathrm{2}} =\frac{\left(\mathrm{2}{b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}\left({b}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}+{y}^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$
Answered by HeferH last updated on 25/Nov/22

Commented by HeferH last updated on 25/Nov/22

