Question Number 181496 by Acem last updated on 26/Nov/22
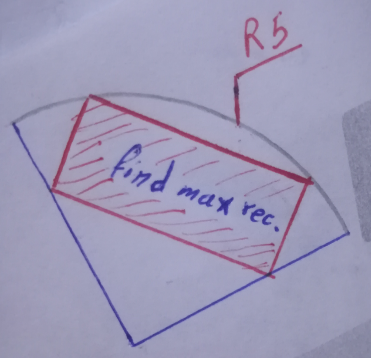
Answered by mr W last updated on 26/Nov/22
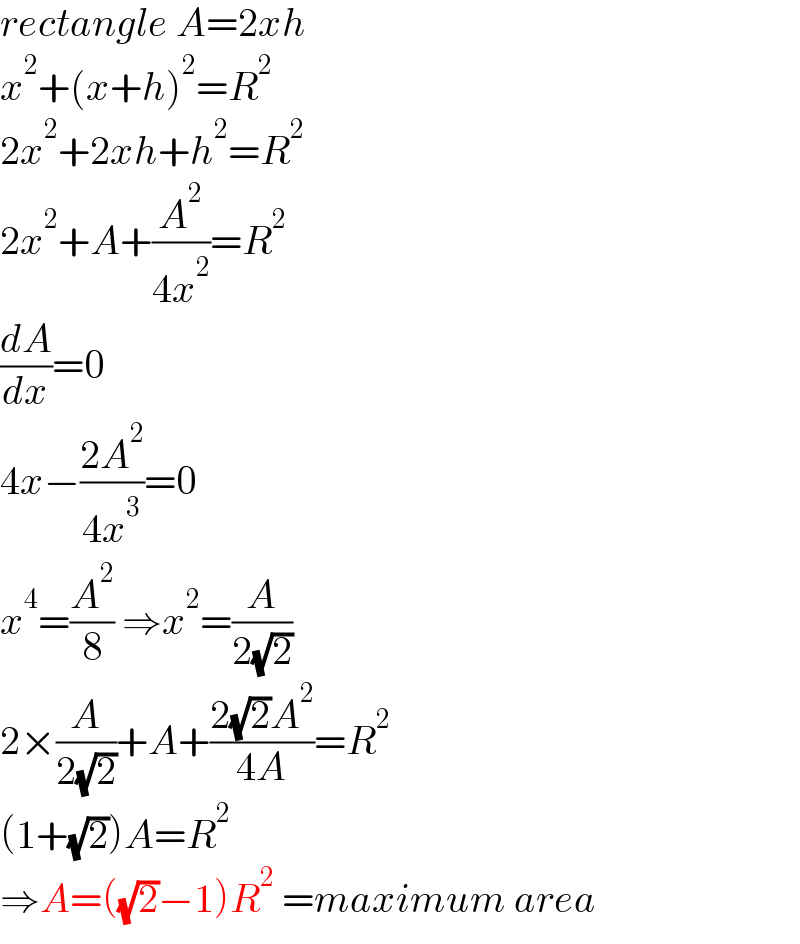
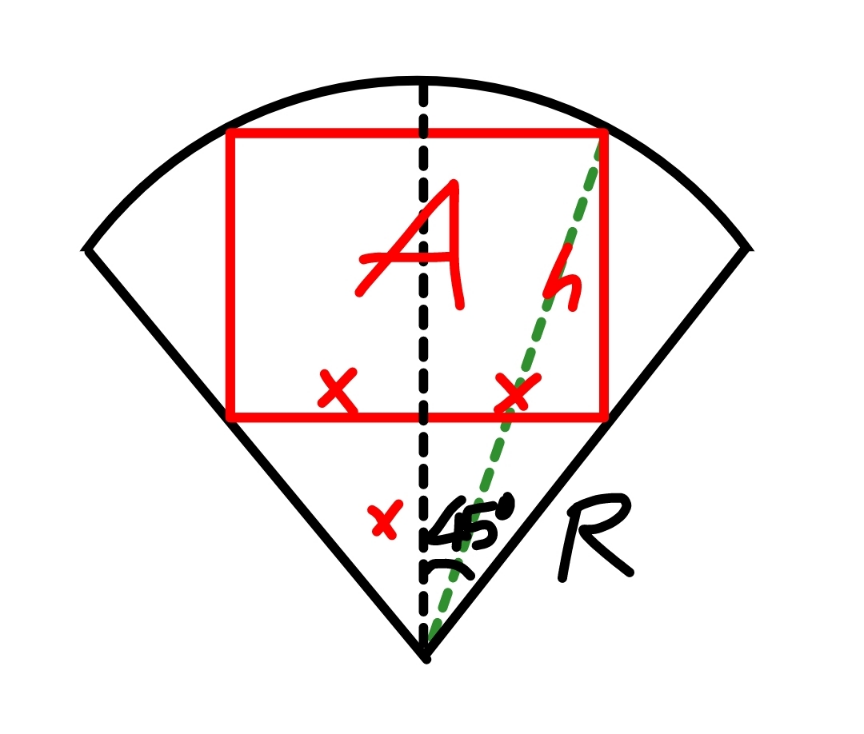
$${rectangle}\:{A}=\mathrm{2}{xh} \\ $$$${x}^{\mathrm{2}} +\left({x}+{h}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{xh}+{h}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +{A}+\frac{{A}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }={R}^{\mathrm{2}} \\ $$$$\frac{{dA}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{4}{x}−\frac{\mathrm{2}{A}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{3}} }=\mathrm{0} \\ $$$${x}^{\mathrm{4}} =\frac{{A}^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow{x}^{\mathrm{2}} =\frac{{A}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{2}×\frac{{A}}{\mathrm{2}\sqrt{\mathrm{2}}}+{A}+\frac{\mathrm{2}\sqrt{\mathrm{2}}{A}^{\mathrm{2}} }{\mathrm{4}{A}}={R}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){A}={R}^{\mathrm{2}} \\ $$$$\Rightarrow{A}=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right){R}^{\mathrm{2}} \:={maximum}\:{area} \\ $$
Commented by mr W last updated on 26/Nov/22