Question Number 181522 by mr W last updated on 26/Nov/22
Commented by mr W last updated on 26/Nov/22

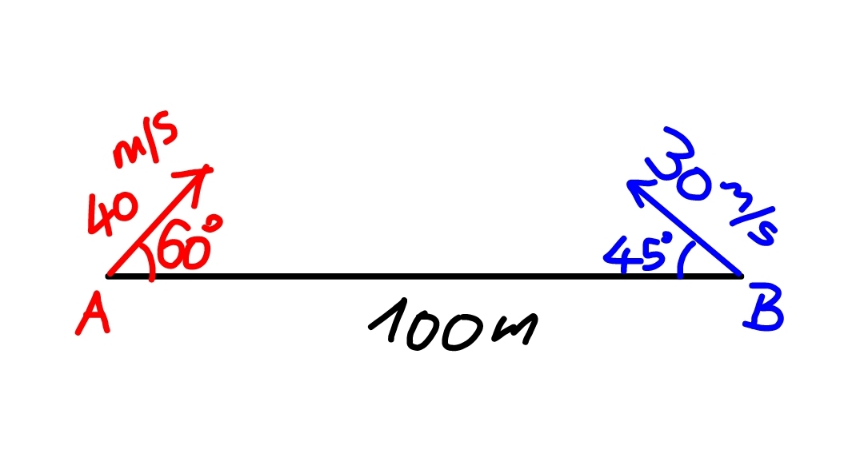
$${two}\:{objects}\:{are}\:{fired}\:{at}\:{the}\:{same}\:{time} \\ $$$${from}\:{point}\:{A}\:{and}\:{point}\:{B}\:{as}\:{shown}. \\ $$$${what}\:{is}\:{the}\:{smallest}\:{distance}\: \\ $$$${between}\:{them}\:{after}\:{which}\:{time}? \\ $$
Answered by mahdipoor last updated on 26/Nov/22

$${V}_{{AB}} ={V}_{{AO}} −{V}_{{BO}} = \\ $$$$\left(\mathrm{40}{cos}\mathrm{60},−{gt}+\mathrm{40}{sin}\mathrm{60}\right)−\left(−\mathrm{30}{cos}\mathrm{45},−{gt}+\mathrm{30}{cos}\mathrm{45}\right)= \\ $$$$\left(\mathrm{20}+\mathrm{15}\sqrt{\mathrm{2}},\mathrm{20}\sqrt{\mathrm{3}}−\mathrm{15}\sqrt{\mathrm{2}}\right) \\ $$$${with}\:{this}\:{speed}\:{we}\:{can}\:{assumed}\:{B}\:{is}\:{fixed}\: \\ $$$${and}\:{A}\:{is}\:{animated}\:{that}\:{speed}\:{is}\:{V}={V}_{{AB}} \\ $$$${trajectory}\:{of}\:{Ais}\:{line}\:,\:{when}\:{AB}\bot{this}\:{line}\:\Rightarrow\:{AB}\:{is}\:{min} \\ $$$${tan}\theta=\frac{\mathrm{20}\sqrt{\mathrm{3}}−\mathrm{15}\sqrt{\mathrm{2}}}{\mathrm{20}+\mathrm{15}\sqrt{\mathrm{2}}}\:,\:\mathrm{100}×{sin}\theta={min}\left({AB}\right) \\ $$$$\Rightarrow\theta\approx\mathrm{18}.\mathrm{04}\:\Rightarrow\:{minAB}\approx\mathrm{30}.\mathrm{97}\:{km} \\ $$
Commented by mr W last updated on 26/Nov/22

$${great}! \\ $$
Answered by mr W last updated on 26/Nov/22
Commented by mr W last updated on 26/Nov/22

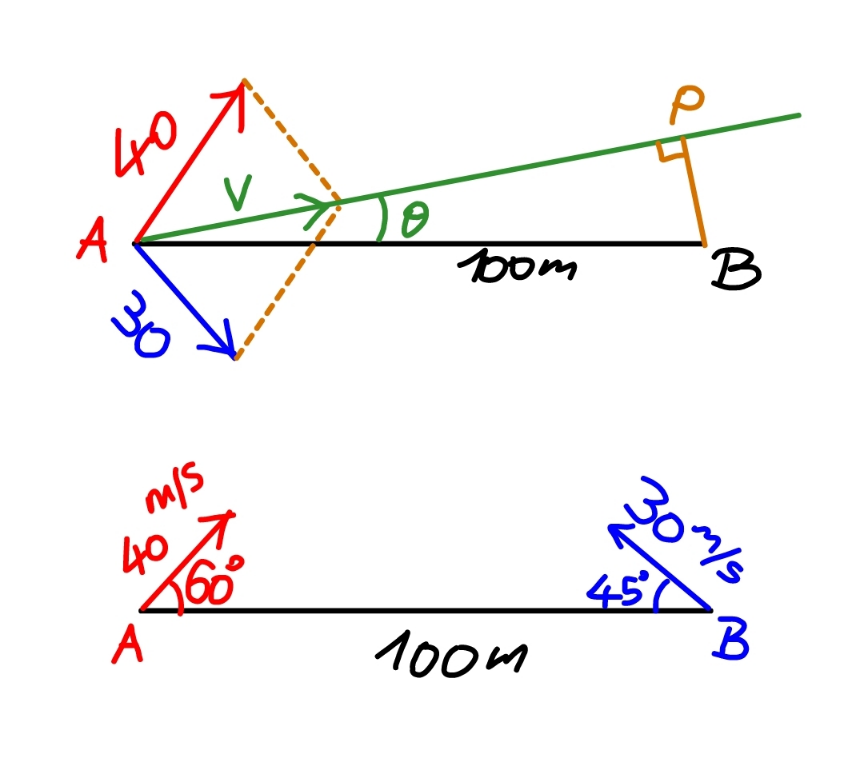
$${using}\:{relative}\:{motion}: \\ $$$${v}_{{x}} =\mathrm{40}\:\mathrm{cos}\:\mathrm{60}°+\mathrm{30}\:\mathrm{cos}\:\mathrm{45}°=\mathrm{20}+\mathrm{15}\sqrt{\mathrm{2}} \\ $$$${v}_{{y}} =\mathrm{40}\:\mathrm{sin}\:\mathrm{60}°−\mathrm{30}\:\mathrm{sin}\:\mathrm{45}°=\mathrm{20}\sqrt{\mathrm{3}}−\mathrm{15}\sqrt{\mathrm{2}} \\ $$$${v}=\sqrt{\left(\mathrm{20}+\mathrm{15}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{20}\sqrt{\mathrm{3}}−\mathrm{15}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{10}\sqrt{\mathrm{25}+\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{6}\sqrt{\mathrm{6}}} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{20}\sqrt{\mathrm{3}}−\mathrm{15}\sqrt{\mathrm{2}}}{\mathrm{20}+\mathrm{15}\sqrt{\mathrm{2}}}=\frac{\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}+\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$${BP}=\mathrm{100}\:\mathrm{sin}\:\theta=\frac{\mathrm{50}\left(\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{25}+\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{6}\sqrt{\mathrm{6}}}}\approx\mathrm{30}.\mathrm{979}\:{m} \\ $$$${AP}=\mathrm{100}\:\mathrm{cos}\:\theta=\frac{\mathrm{50}\left(\mathrm{4}+\mathrm{3}\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{25}+\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{6}\sqrt{\mathrm{6}}}} \\ $$$${t}=\frac{\mathrm{50}\left(\mathrm{4}+\mathrm{3}\sqrt{\mathrm{2}}\right)}{\:\mathrm{10}\sqrt{\left(\mathrm{25}+\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{6}\sqrt{\mathrm{6}}\right)\left(\mathrm{25}+\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{6}\sqrt{\mathrm{6}}\right)}} \\ $$$$\:=\frac{\mathrm{5}\left(\mathrm{4}+\mathrm{3}\sqrt{\mathrm{2}}\right)}{\:\mathrm{25}+\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{6}\sqrt{\mathrm{6}}}\approx\mathrm{2}.\mathrm{194}\:{s} \\ $$
Commented by mr W last updated on 26/Nov/22

