Question-181673

Question Number 181673 by cherokeesay last updated on 28/Nov/22

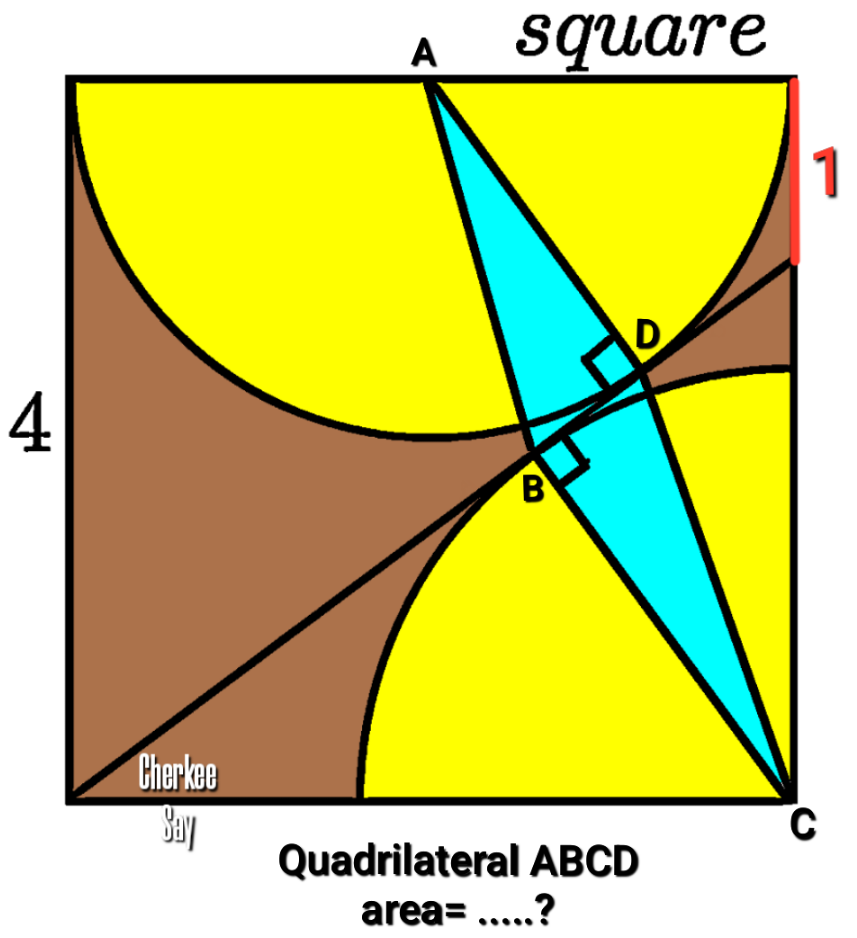
Answered by HeferH last updated on 28/Nov/22

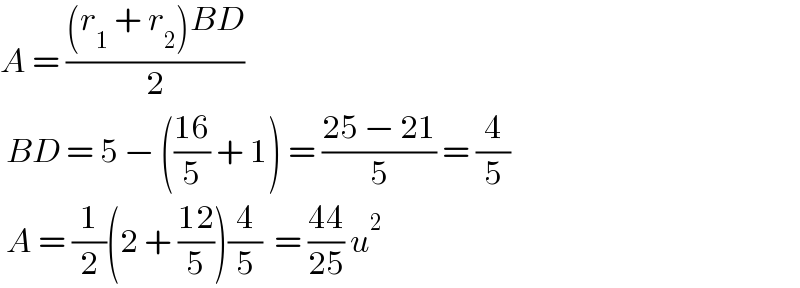
A = (((r_1 + r_2 )BD)/2) BD = 5 − (((16)/5) + 1) = ((25 − 21)/5) = (4/5) A = (1/2)(2 + ((12)/5))(4/5) = ((44)/(25)) u^2

$${A}\:=\:\frac{\left({r}_{\mathrm{1}} \:+\:{r}_{\mathrm{2}} \right){BD}}{\mathrm{2}}\: \\ $$$$\:{BD}\:=\:\mathrm{5}\:−\:\left(\frac{\mathrm{16}}{\mathrm{5}}\:+\:\mathrm{1}\right)\:=\:\frac{\mathrm{25}\:−\:\mathrm{21}}{\mathrm{5}}\:=\:\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\:{A}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\:+\:\frac{\mathrm{12}}{\mathrm{5}}\right)\frac{\mathrm{4}}{\mathrm{5}}\:\:=\:\frac{\mathrm{44}}{\mathrm{25}}\:{u}^{\mathrm{2}} \\ $$

Commented by cherokeesay last updated on 29/Nov/22

$${Nice}\:{solution}, \\ $$$${thank}\:{you}\:{sir}. \\ $$

Answered by a.lgnaoui last updated on 29/Nov/22

$${Area}=\mathrm{1},\mathrm{76} \\ $$

Answered by a.lgnaoui last updated on 29/Nov/22

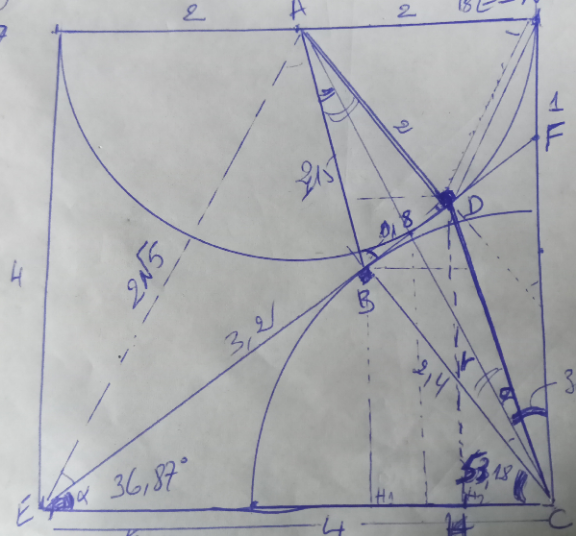
Answered by a.lgnaoui last updated on 29/Nov/22

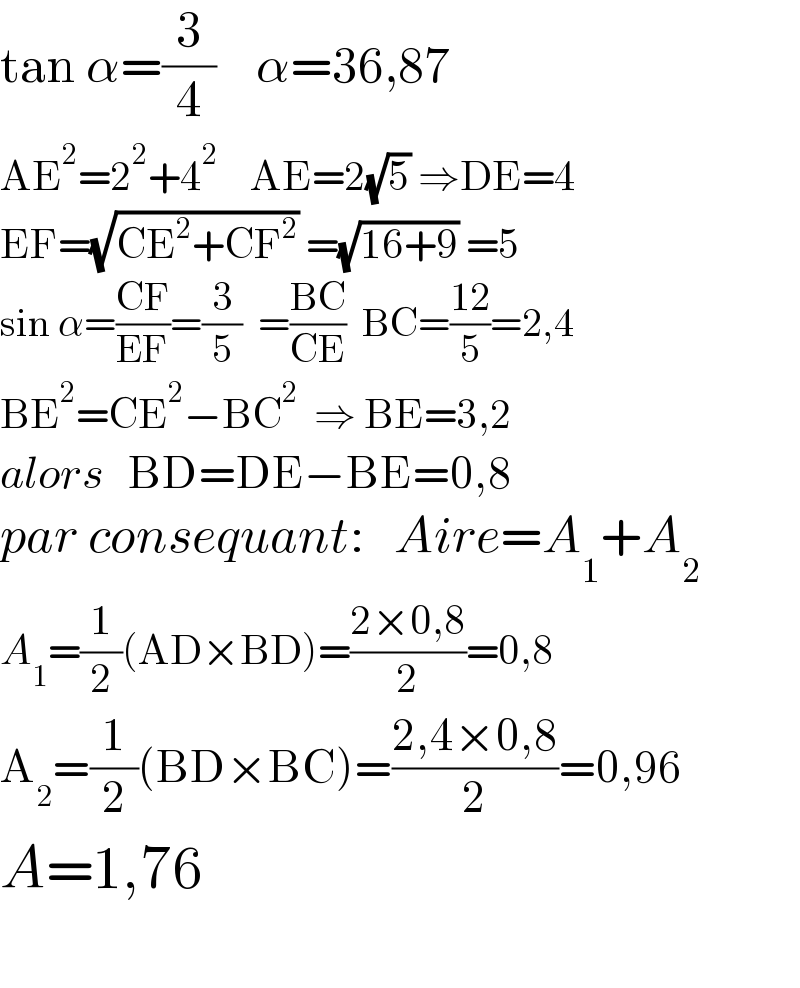
tan α=(3/4) α=36,87 AE^2 =2^2 +4^2 AE=2(√5) ⇒DE=4 EF=(√(CE^2 +CF^2 )) =(√(16+9)) =5 sin α=((CF)/(EF))=(3/5) =((BC)/(CE)) BC=((12)/5)=2,4 BE^2 =CE^2 −BC^2 ⇒ BE=3,2 alors BD=DE−BE=0,8 par consequant: Aire=A_1 +A_2 A_1 =(1/2)(AD×BD)=((2×0,8)/2)=0,8 A_2 =(1/2)(BD×BC)=((2,4×0,8)/2)=0,96 A=1,76

$$\mathrm{tan}\:\alpha=\frac{\mathrm{3}}{\mathrm{4}}\:\:\:\:\alpha=\mathrm{36},\mathrm{87} \\ $$$$\mathrm{AE}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} \:\:\:\:\mathrm{AE}=\mathrm{2}\sqrt{\mathrm{5}}\:\Rightarrow\mathrm{DE}=\mathrm{4} \\ $$$$\mathrm{EF}=\sqrt{\mathrm{CE}^{\mathrm{2}} +\mathrm{CF}^{\mathrm{2}} }\:=\sqrt{\mathrm{16}+\mathrm{9}}\:=\mathrm{5} \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{CF}}{\mathrm{EF}}=\frac{\mathrm{3}}{\mathrm{5}}\:\:=\frac{\mathrm{BC}}{\mathrm{CE}}\:\:\mathrm{BC}=\frac{\mathrm{12}}{\mathrm{5}}=\mathrm{2},\mathrm{4} \\ $$$$\mathrm{BE}^{\mathrm{2}} =\mathrm{CE}^{\mathrm{2}} −\mathrm{BC}^{\mathrm{2}} \:\:\Rightarrow\:\mathrm{BE}=\mathrm{3},\mathrm{2} \\ $$$${alors}\:\:\:\mathrm{BD}=\mathrm{DE}−\mathrm{BE}=\mathrm{0},\mathrm{8} \\ $$$${par}\:{consequant}:\:\:\:{Aire}={A}_{\mathrm{1}} +{A}_{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{AD}×\mathrm{BD}\right)=\frac{\mathrm{2}×\mathrm{0},\mathrm{8}}{\mathrm{2}}=\mathrm{0},\mathrm{8} \\ $$$$\mathrm{A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{BD}×\mathrm{BC}\right)=\frac{\mathrm{2},\mathrm{4}×\mathrm{0},\mathrm{8}}{\mathrm{2}}=\mathrm{0},\mathrm{96} \\ $$$${A}=\mathrm{1},\mathrm{76} \\ $$$$ \\ $$

Commented by cherokeesay last updated on 29/Nov/22

$${Nice}\:! \\ $$$${thank}\:{you}\:{so}\:{much}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply