Question-181676

Question Number 181676 by yaslm last updated on 28/Nov/22

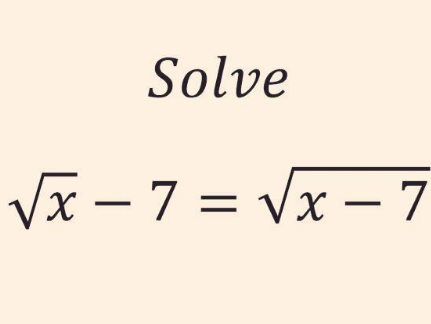
Answered by floor(10²Eta[1]) last updated on 28/Nov/22

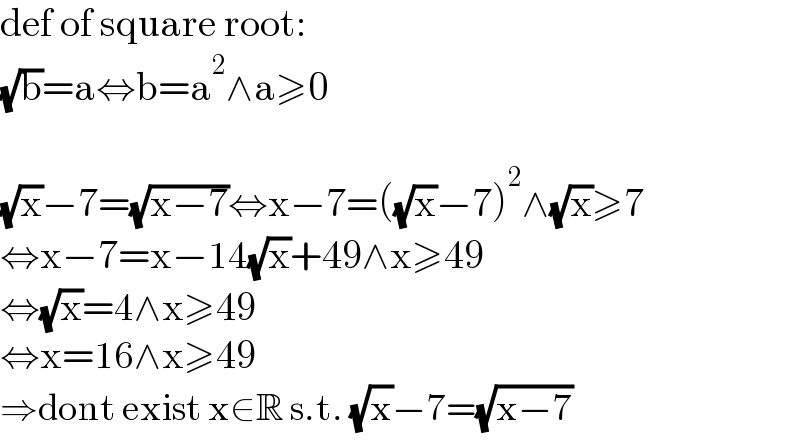
def of square root: (√b)=a⇔b=a^2 ∧a≥0 (√x)−7=(√(x−7))⇔x−7=((√x)−7)^2 ∧(√x)≥7 ⇔x−7=x−14(√x)+49∧x≥49 ⇔(√x)=4∧x≥49 ⇔x=16∧x≥49 ⇒dont exist x∈R s.t. (√x)−7=(√(x−7))

$$\mathrm{def}\:\mathrm{of}\:\mathrm{square}\:\mathrm{root}: \\ $$$$\sqrt{\mathrm{b}}=\mathrm{a}\Leftrightarrow\mathrm{b}=\mathrm{a}^{\mathrm{2}} \wedge\mathrm{a}\geqslant\mathrm{0} \\ $$$$ \\ $$$$\sqrt{\mathrm{x}}−\mathrm{7}=\sqrt{\mathrm{x}−\mathrm{7}}\Leftrightarrow\mathrm{x}−\mathrm{7}=\left(\sqrt{\mathrm{x}}−\mathrm{7}\right)^{\mathrm{2}} \wedge\sqrt{\mathrm{x}}\geqslant\mathrm{7} \\ $$$$\Leftrightarrow\mathrm{x}−\mathrm{7}=\mathrm{x}−\mathrm{14}\sqrt{\mathrm{x}}+\mathrm{49}\wedge\mathrm{x}\geqslant\mathrm{49} \\ $$$$\Leftrightarrow\sqrt{\mathrm{x}}=\mathrm{4}\wedge\mathrm{x}\geqslant\mathrm{49} \\ $$$$\Leftrightarrow\mathrm{x}=\mathrm{16}\wedge\mathrm{x}\geqslant\mathrm{49} \\ $$$$\Rightarrow\mathrm{dont}\:\mathrm{exist}\:\mathrm{x}\in\mathbb{R}\:\mathrm{s}.\mathrm{t}.\:\sqrt{\mathrm{x}}−\mathrm{7}=\sqrt{\mathrm{x}−\mathrm{7}} \\ $$

Commented by yaslm last updated on 28/Nov/22

great sir

Answered by Rasheed.Sindhi last updated on 30/Nov/22

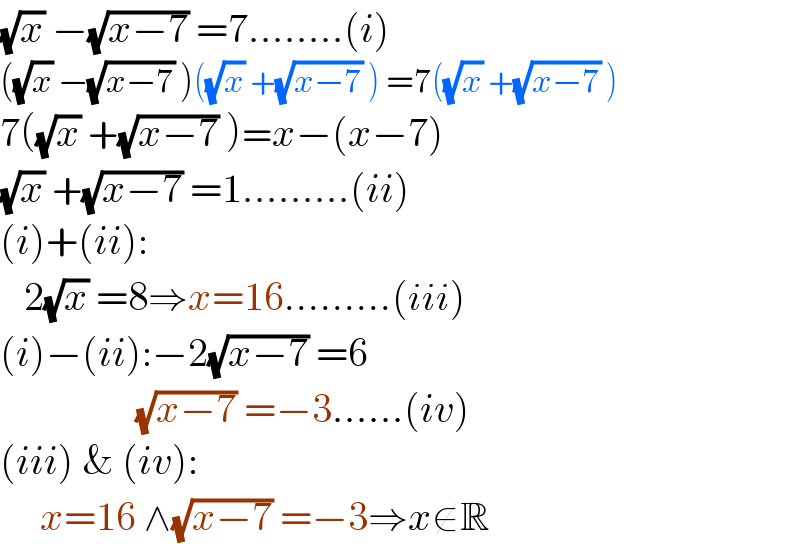
(√x) −(√(x−7)) =7........(i) ((√x) −(√(x−7)) )((√x) +(√(x−7)) ) =7((√x) +(√(x−7)) ) 7((√x) +(√(x−7)) )=x−(x−7) (√x) +(√(x−7)) =1.........(ii) (i)+(ii): 2(√x) =8⇒x=16.........(iii) (i)−(ii):−2(√(x−7)) =6 (√(x−7)) =−3......(iv) (iii) & (iv): x=16 ∧(√(x−7)) =−3⇒x∉R

$$\sqrt{{x}}\:−\sqrt{{x}−\mathrm{7}}\:=\mathrm{7}……..\left({i}\right) \\ $$$$\left(\sqrt{{x}}\:−\sqrt{{x}−\mathrm{7}}\:\right)\left(\sqrt{{x}}\:+\sqrt{{x}−\mathrm{7}}\:\right)\:=\mathrm{7}\left(\sqrt{{x}}\:+\sqrt{{x}−\mathrm{7}}\:\right) \\ $$$$\mathrm{7}\left(\sqrt{{x}}\:+\sqrt{{x}−\mathrm{7}}\:\right)={x}−\left({x}−\mathrm{7}\right) \\ $$$$\sqrt{{x}}\:+\sqrt{{x}−\mathrm{7}}\:=\mathrm{1}………\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\:\:\:\mathrm{2}\sqrt{{x}}\:=\mathrm{8}\Rightarrow{x}=\mathrm{16}………\left({iii}\right) \\ $$$$\left({i}\right)−\left({ii}\right):−\mathrm{2}\sqrt{{x}−\mathrm{7}}\:=\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{{x}−\mathrm{7}}\:=−\mathrm{3}……\left({iv}\right) \\ $$$$\left({iii}\right)\:\&\:\left({iv}\right): \\ $$$$\:\:\:\:\:{x}=\mathrm{16}\:\wedge\sqrt{{x}−\mathrm{7}}\:=−\mathrm{3}\Rightarrow{x}\notin\mathbb{R}\: \\ $$

Commented by Frix last updated on 29/Nov/22

you must test your solution (√(16))−(√(16−7))=7 (√(16))−(√9)=7 4−3=7 wrong

$$\mathrm{you}\:\mathrm{must}\:\mathrm{test}\:\mathrm{your}\:\mathrm{solution} \\ $$$$\sqrt{\mathrm{16}}−\sqrt{\mathrm{16}−\mathrm{7}}=\mathrm{7} \\ $$$$\sqrt{\mathrm{16}}−\sqrt{\mathrm{9}}=\mathrm{7} \\ $$$$\mathrm{4}−\mathrm{3}=\mathrm{7}\:\mathrm{wrong} \\ $$

Commented by Rasheed.Sindhi last updated on 30/Nov/22

Forgot that I ′ve squared both sides. ...Of course the solution is incorrect! ThanX much sir!

$${Forgot}\:{that}\:{I}\:'{ve}\:{squared}\:{both}\:{sides}. \\ $$$$…{Of}\:{course}\:\:{the}\:{solution}\:{is}\:{incorrect}!\: \\ $$$$\mathcal{T}{han}\mathcal{X}\:{much}\:{sir}! \\ $$

Commented by Rasheed.Sindhi last updated on 30/Nov/22

$$…{Had}\:{I}\:{studied}\:{sir}\:{floor}'{s}\:{answer} \\ $$$${properly}! \\ $$

Commented by Rasheed.Sindhi last updated on 30/Nov/22

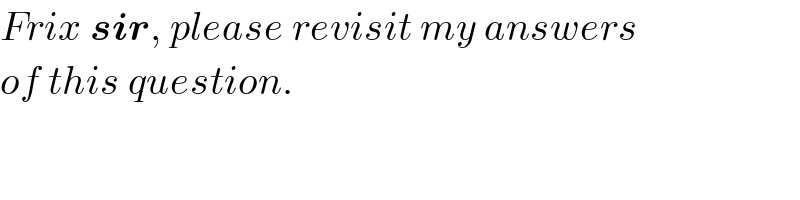
Frix sir, please revisit my answers of this question.

$${Frix}\:\boldsymbol{{sir}},\:{please}\:{revisit}\:{my}\:{answers} \\ $$$${of}\:{this}\:{question}. \\ $$

Commented by Frix last updated on 30/Nov/22

Sorry I get no notifications from this app, so I′m a bit late... your answers are now correct.

$$\mathrm{Sorry}\:\mathrm{I}\:\mathrm{get}\:\mathrm{no}\:\mathrm{notifications}\:\mathrm{from}\:\mathrm{this}\:\mathrm{app}, \\ $$$$\mathrm{so}\:\mathrm{I}'\mathrm{m}\:\mathrm{a}\:\mathrm{bit}\:\mathrm{late}…\:\mathrm{your}\:\mathrm{answers}\:\mathrm{are}\:\mathrm{now} \\ $$$$\mathrm{correct}. \\ $$

Commented by Rasheed.Sindhi last updated on 01/Dec/22

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{lot}}\:\boldsymbol{\mathrm{sir}}! \\ $$

Answered by Rasheed.Sindhi last updated on 30/Nov/22

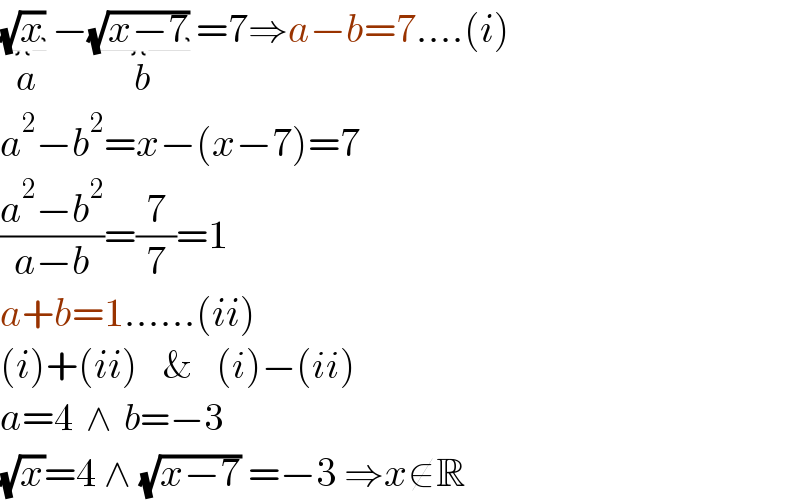
(√x) _(a) −(√(x−7)) _(b) =7⇒a−b=7....(i) a^2 −b^2 =x−(x−7)=7 ((a^2 −b^2 )/(a−b))=(7/7)=1 a+b=1......(ii) (i)+(ii) & (i)−(ii) a=4 ∧ b=−3 (√x)=4 ∧ (√(x−7)) =−3 ⇒x∉R

$$\underset{{a}} {\underbrace{\sqrt{{x}}\:}}−\underset{{b}} {\underbrace{\sqrt{{x}−\mathrm{7}}\:}}=\mathrm{7}\Rightarrow{a}−{b}=\mathrm{7}….\left({i}\right) \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={x}−\left({x}−\mathrm{7}\right)=\mathrm{7} \\ $$$$\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}−{b}}=\frac{\mathrm{7}}{\mathrm{7}}=\mathrm{1} \\ $$$${a}+{b}=\mathrm{1}……\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right)\:\:\:\:\&\:\:\:\:\left({i}\right)−\left({ii}\right) \\ $$$${a}=\mathrm{4}\:\:\wedge\:\:{b}=−\mathrm{3} \\ $$$$\sqrt{{x}}=\mathrm{4}\:\wedge\:\sqrt{{x}−\mathrm{7}}\:=−\mathrm{3}\:\Rightarrow{x}\notin\mathbb{R} \\ $$

Answered by Frix last updated on 30/Nov/22

For x, a ∈R (√x)−a=(√(x−a)) Squaring both sides x−2a(√x)+a^2 =x−a 2a(√x)−a(a+1)=0 a=0 is a solution 2(√x)−(a+1)=0 x=(((a+1)^2 )/4)∧a+1≥0 Inserting this in the given equation gives ((∣a+1∣)/2)−a=((∣a−1∣)/2) This is true for −1≤a≤1 ⇒ (√x)−a=(√(x−a)) can only be solved for −1≤a≤1

$$\mathrm{For}\:{x},\:{a}\:\in\mathbb{R} \\ $$$$\sqrt{{x}}−{a}=\sqrt{{x}−{a}} \\ $$$$\mathrm{Squaring}\:\mathrm{both}\:\mathrm{sides} \\ $$$${x}−\mathrm{2}{a}\sqrt{{x}}+{a}^{\mathrm{2}} ={x}−{a} \\ $$$$\mathrm{2}{a}\sqrt{{x}}−{a}\left({a}+\mathrm{1}\right)=\mathrm{0} \\ $$$${a}=\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$$$\mathrm{2}\sqrt{{x}}−\left({a}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\frac{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\wedge{a}+\mathrm{1}\geqslant\mathrm{0} \\ $$$$\mathrm{Inserting}\:\mathrm{this}\:\mathrm{in}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{gives} \\ $$$$\frac{\mid{a}+\mathrm{1}\mid}{\mathrm{2}}−{a}=\frac{\mid{a}−\mathrm{1}\mid}{\mathrm{2}} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:−\mathrm{1}\leqslant{a}\leqslant\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\sqrt{{x}}−{a}=\sqrt{{x}−{a}}\:\mathrm{can}\:\mathrm{only}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:−\mathrm{1}\leqslant{a}\leqslant\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply