Question Number 181711 by Ari last updated on 28/Nov/22

Commented by mr W last updated on 29/Nov/22
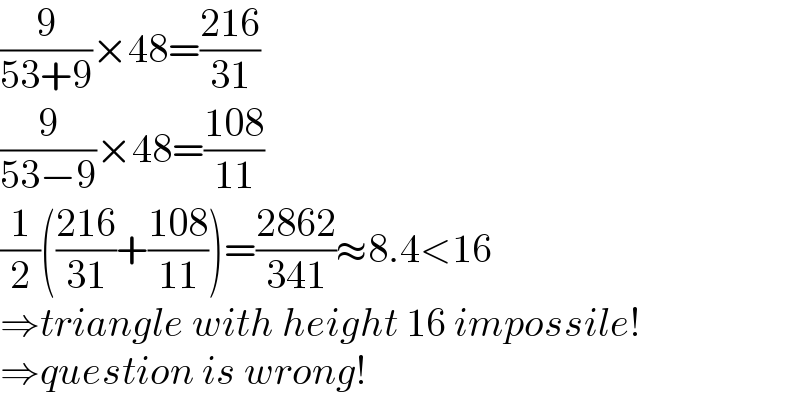
$$\frac{\mathrm{9}}{\mathrm{53}+\mathrm{9}}×\mathrm{48}=\frac{\mathrm{216}}{\mathrm{31}} \\ $$$$\frac{\mathrm{9}}{\mathrm{53}−\mathrm{9}}×\mathrm{48}=\frac{\mathrm{108}}{\mathrm{11}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{216}}{\mathrm{31}}+\frac{\mathrm{108}}{\mathrm{11}}\right)=\frac{\mathrm{2862}}{\mathrm{341}}\approx\mathrm{8}.\mathrm{4}<\mathrm{16} \\ $$$$\Rightarrow{triangle}\:{with}\:{height}\:\mathrm{16}\:{impossile}! \\ $$$$\Rightarrow{question}\:{is}\:{wrong}! \\ $$
Commented by Ari last updated on 29/Nov/22

Commented by mr W last updated on 29/Nov/22

Commented by mr W last updated on 29/Nov/22

$$\boldsymbol{{Method}}\:\boldsymbol{{I}} \\ $$$${say}\:{the}\:{two}\:{unknown}\:{sides}\:{are}\:{x},\:{y}. \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{9}}{\mathrm{53}}\:\:\:…\left({i}\right) \\ $$$$\sqrt{{x}^{\mathrm{2}} −\mathrm{16}^{\mathrm{2}} }+\sqrt{{y}^{\mathrm{2}} −\mathrm{16}^{\mathrm{2}} }=\mathrm{48}\:\:\:…\left({ii}\right) \\ $$$${we}\:{get}\:{from}\:\left({i}\right)\:{y}=\frac{\mathrm{53}{x}}{\mathrm{9}}\:{and}\:{put}\:{this} \\ $$$${into}\:\left({ii}\right).\:{we}\:{get}\:{a}\:{quadratic}\:{eqn}.\:{for} \\ $$$${x}^{\mathrm{2}} .\:{we}'{ll}\:{see}\:{it}\:{has}\:{not}\:{real}\:{roots}. \\ $$
Commented by mr W last updated on 29/Nov/22

Commented by mr W last updated on 29/Nov/22

$$\boldsymbol{{Method}}\:\boldsymbol{{II}} \\ $$$${BC}=\mathrm{48} \\ $$$${for}\:\frac{{BA}}{{CA}}=\frac{\mathrm{9}}{\mathrm{53}}={constant},\:{the}\:{locus}\:{of} \\ $$$${point}\:{A}\:{is}\:{a}\:{circle}\:{as}\:{shown}. \\ $$$$\frac{{BD}}{{CD}}=\frac{\mathrm{9}}{\mathrm{53}} \\ $$$$\Rightarrow{BD}=\frac{\mathrm{9}}{\mathrm{53}+\mathrm{9}}×{BC}=\frac{\mathrm{9}}{\mathrm{53}+\mathrm{9}}×\mathrm{48}=\frac{\mathrm{216}}{\mathrm{31}} \\ $$$$\frac{{BE}}{{CE}}=\frac{\mathrm{9}}{\mathrm{53}} \\ $$$$\Rightarrow{BE}=\frac{\mathrm{9}}{\mathrm{53}−\mathrm{9}}×{BC}=\frac{\mathrm{9}}{\mathrm{53}−\mathrm{9}}×\mathrm{48}=\frac{\mathrm{108}}{\mathrm{11}} \\ $$$${OB}={OD}={radius}=\frac{{BD}+{BE}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{216}}{\mathrm{31}}+\frac{\mathrm{108}}{\mathrm{11}}\right)=\frac{\mathrm{2862}}{\mathrm{341}}\approx\mathrm{8}.\mathrm{39} \\ $$$${the}\:{largest}\:{possible}\:{height}\:{of}\:{the} \\ $$$${triangle}\:{is}\:{OA}'={radius}\approx\mathrm{8}.\mathrm{39}<\mathrm{16}. \\ $$$${that}\:{means}\:{the}\:{triangle}\:{can}\:{never} \\ $$$${have}\:{a}\:{height}\:{of}\:\mathrm{16}. \\ $$
Commented by Ari last updated on 29/Nov/22
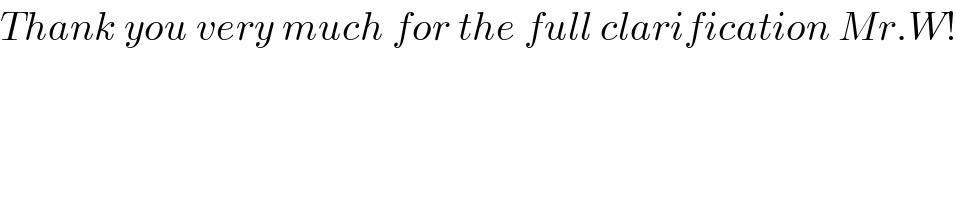
$${Thank}\:{you}\:{very}\:{much}\:{for}\:{the}\:{full}\:{clarification}\:{Mr}.{W}! \\ $$
Commented by mr W last updated on 30/Nov/22
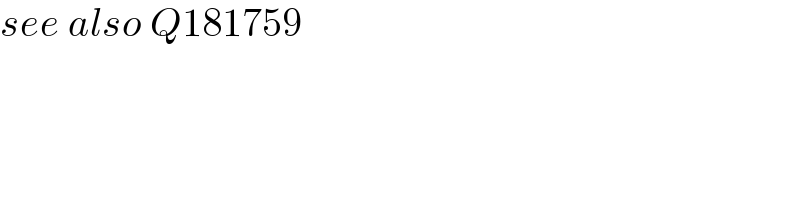
$${see}\:{also}\:{Q}\mathrm{181759} \\ $$
Commented by mr W last updated on 30/Nov/22
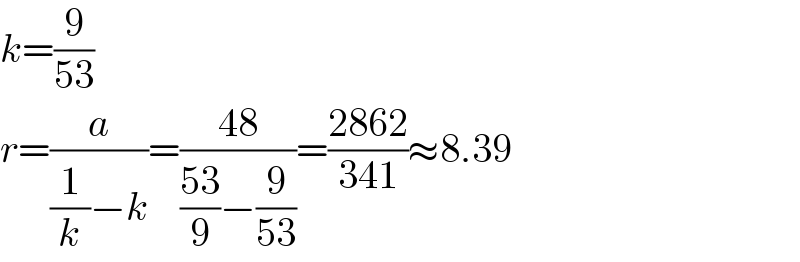
$${k}=\frac{\mathrm{9}}{\mathrm{53}} \\ $$$${r}=\frac{{a}}{\frac{\mathrm{1}}{{k}}−{k}}=\frac{\mathrm{48}}{\frac{\mathrm{53}}{\mathrm{9}}−\frac{\mathrm{9}}{\mathrm{53}}}=\frac{\mathrm{2862}}{\mathrm{341}}\approx\mathrm{8}.\mathrm{39} \\ $$
