Question Number 181741 by yaslm last updated on 29/Nov/22

Answered by cortano1 last updated on 30/Nov/22
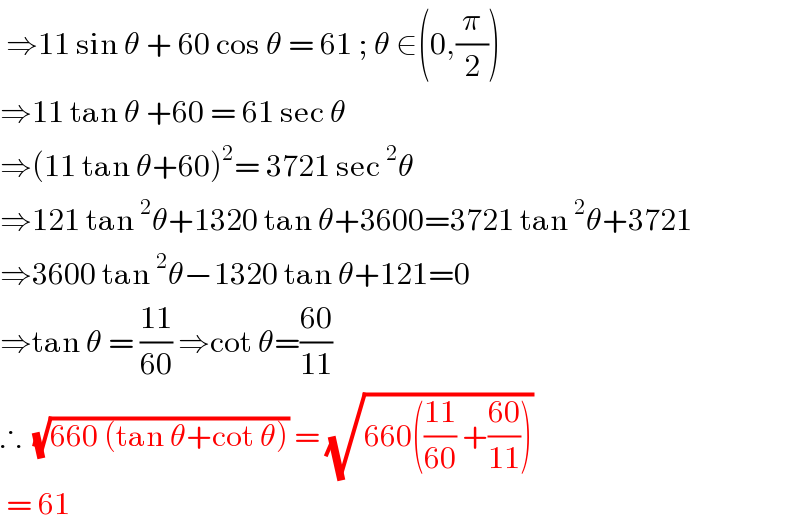
$$\:\Rightarrow\mathrm{11}\:\mathrm{sin}\:\theta\:+\:\mathrm{60}\:\mathrm{cos}\:\theta\:=\:\mathrm{61}\:;\:\theta\:\in\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{11}\:\mathrm{tan}\:\theta\:+\mathrm{60}\:=\:\mathrm{61}\:\mathrm{sec}\:\theta\: \\ $$$$\Rightarrow\left(\mathrm{11}\:\mathrm{tan}\:\theta+\mathrm{60}\right)^{\mathrm{2}} =\:\mathrm{3721}\:\mathrm{sec}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\mathrm{121}\:\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{1320}\:\mathrm{tan}\:\theta+\mathrm{3600}=\mathrm{3721}\:\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{3721} \\ $$$$\Rightarrow\mathrm{3600}\:\mathrm{tan}\:^{\mathrm{2}} \theta−\mathrm{1320}\:\mathrm{tan}\:\theta+\mathrm{121}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta\:=\:\frac{\mathrm{11}}{\mathrm{60}}\:\Rightarrow\mathrm{cot}\:\theta=\frac{\mathrm{60}}{\mathrm{11}} \\ $$$$\therefore\:\:\sqrt{\mathrm{660}\:\left(\mathrm{tan}\:\theta+\mathrm{cot}\:\theta\right)}\:=\:\sqrt{\mathrm{660}\left(\frac{\mathrm{11}}{\mathrm{60}}\:+\frac{\mathrm{60}}{\mathrm{11}}\right)} \\ $$$$\:=\:\mathrm{61}\: \\ $$
