Question Number 181759 by mr W last updated on 29/Nov/22
Commented by mr W last updated on 30/Nov/22
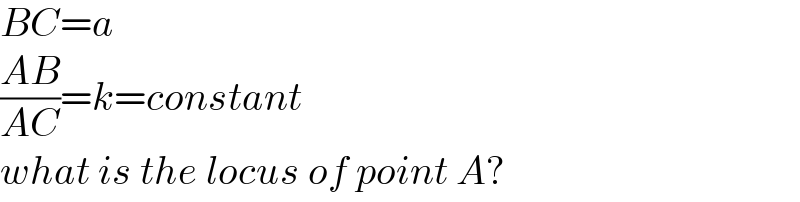
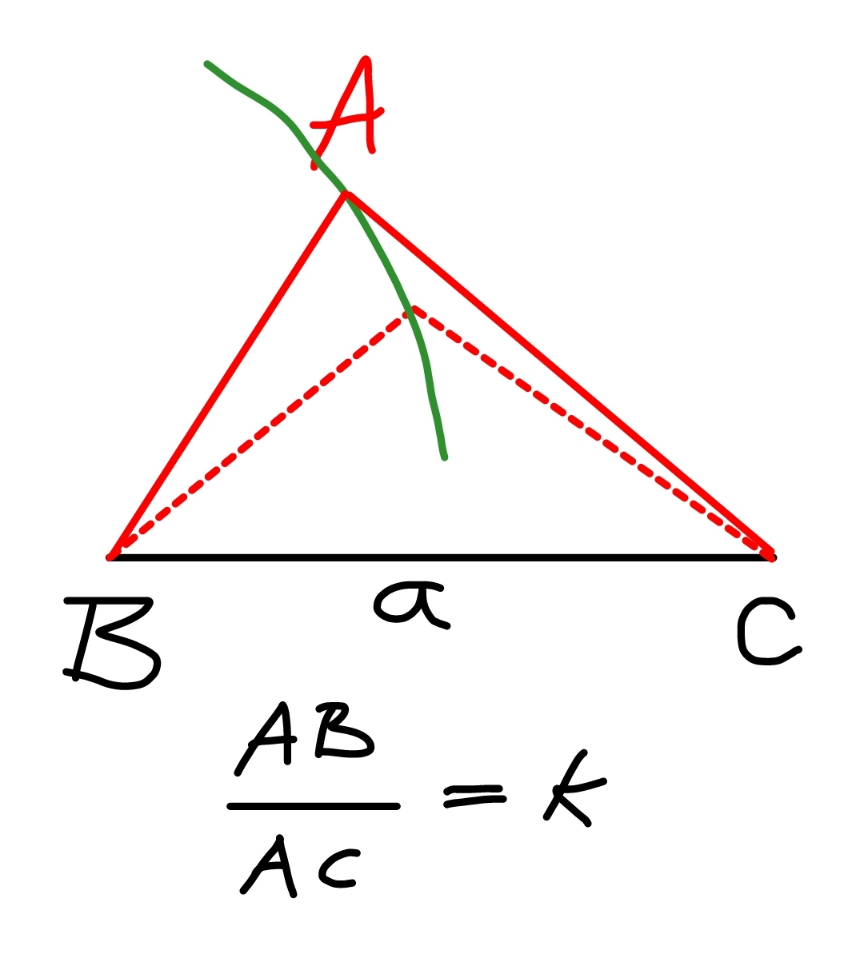
$${BC}={a} \\ $$$$\frac{{AB}}{{AC}}={k}={constant} \\ $$$${what}\:{is}\:{the}\:{locus}\:{of}\:{point}\:{A}? \\ $$
Answered by mr W last updated on 30/Nov/22

Commented by mr W last updated on 30/Nov/22
![if k=1, the locus of A is the perpendicular bisector of BC. now we assume k<1. c^2 =d^2 +e^2 −2de cos θ b^2 =d^2 +(a+e)^2 −2d(a+e) cos θ ((c/b))^2 =((d^2 +e^2 −2de cos θ)/(d^2 +(a+e)^2 −2d(a+e) cos θ))=k^2 k^2 d^2 +k^2 (a+e)^2 −2k^2 d(a+e) cos θ=d^2 +e^2 −2de cos θ (1−k^2 )d^2 +e^2 −k^2 (a+e)^2 =2d[(1−k^2 )e−k^2 a] cos θ set (1−k^2 )e−k^2 a=0, i.e. e=((k^2 a)/(1−k^2 ))=(a/((1/k^2 )−1)) (1−k^2 )d^2 +e^2 −k^2 (a+e)^2 =0 (1−k^2 )d^2 −((k^2 a^2 )/(1−k^2 ))=0 ⇒d=((ka)/(1−k^2 ))=(a/((1/k)−k))=constant that means the locus of A is a circle with radius (a/((1/k)−k)) and center at point D with distance (a/((1/k^2 )−1)) to point B.](https://www.tinkutara.com/question/Q181776.png)
$${if}\:{k}=\mathrm{1},\:{the}\:{locus}\:{of}\:{A}\:{is}\:{the}\: \\ $$$${perpendicular}\:{bisector}\:{of}\:{BC}. \\ $$$${now}\:{we}\:{assume}\:{k}<\mathrm{1}. \\ $$$${c}^{\mathrm{2}} ={d}^{\mathrm{2}} +{e}^{\mathrm{2}} −\mathrm{2}{de}\:\mathrm{cos}\:\theta \\ $$$${b}^{\mathrm{2}} ={d}^{\mathrm{2}} +\left({a}+{e}\right)^{\mathrm{2}} −\mathrm{2}{d}\left({a}+{e}\right)\:\mathrm{cos}\:\theta \\ $$$$\left(\frac{{c}}{{b}}\right)^{\mathrm{2}} =\frac{{d}^{\mathrm{2}} +{e}^{\mathrm{2}} −\mathrm{2}{de}\:\mathrm{cos}\:\theta}{{d}^{\mathrm{2}} +\left({a}+{e}\right)^{\mathrm{2}} −\mathrm{2}{d}\left({a}+{e}\right)\:\mathrm{cos}\:\theta}={k}^{\mathrm{2}} \: \\ $$$${k}^{\mathrm{2}} {d}^{\mathrm{2}} +{k}^{\mathrm{2}} \left({a}+{e}\right)^{\mathrm{2}} −\mathrm{2}{k}^{\mathrm{2}} {d}\left({a}+{e}\right)\:\mathrm{cos}\:\theta={d}^{\mathrm{2}} +{e}^{\mathrm{2}} −\mathrm{2}{de}\:\mathrm{cos}\:\theta \\ $$$$\left(\mathrm{1}−{k}^{\mathrm{2}} \right){d}^{\mathrm{2}} +{e}^{\mathrm{2}} −{k}^{\mathrm{2}} \left({a}+{e}\right)^{\mathrm{2}} =\mathrm{2}{d}\left[\left(\mathrm{1}−{k}^{\mathrm{2}} \right){e}−{k}^{\mathrm{2}} {a}\right]\:\mathrm{cos}\:\theta \\ $$$${set}\:\left(\mathrm{1}−{k}^{\mathrm{2}} \right){e}−{k}^{\mathrm{2}} {a}=\mathrm{0},\:{i}.{e}.\:{e}=\frac{{k}^{\mathrm{2}} {a}}{\mathrm{1}−{k}^{\mathrm{2}} }=\frac{{a}}{\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{1}} \\ $$$$\left(\mathrm{1}−{k}^{\mathrm{2}} \right){d}^{\mathrm{2}} +{e}^{\mathrm{2}} −{k}^{\mathrm{2}} \left({a}+{e}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{1}−{k}^{\mathrm{2}} \right){d}^{\mathrm{2}} −\frac{{k}^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{1}−{k}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{d}=\frac{{ka}}{\mathrm{1}−{k}^{\mathrm{2}} }=\frac{{a}}{\frac{\mathrm{1}}{{k}}−{k}}={constant} \\ $$$${that}\:{means}\:{the}\:{locus}\:{of}\:{A}\:{is}\:{a}\:{circle} \\ $$$${with}\:{radius}\:\frac{{a}}{\frac{\mathrm{1}}{{k}}−{k}}\:{and}\:{center}\:{at}\:{point} \\ $$$${D}\:{with}\:{distance}\:\frac{{a}}{\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{1}}\:{to}\:{point}\:{B}. \\ $$
Answered by A5T last updated on 09/Apr/24
Commented by A5T last updated on 09/Apr/24
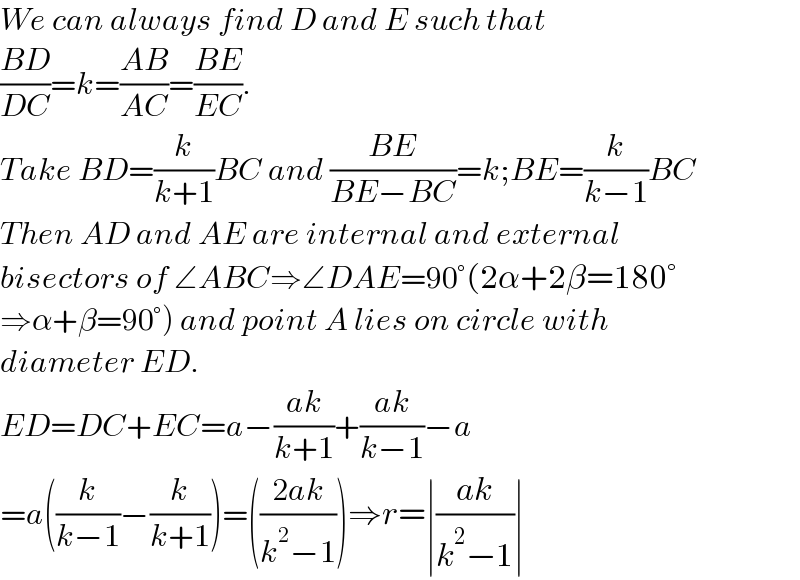
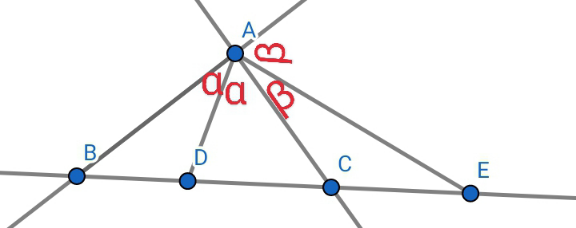
$${We}\:{can}\:{always}\:{find}\:{D}\:{and}\:{E}\:{such}\:{that} \\ $$$$\frac{{BD}}{{DC}}={k}=\frac{{AB}}{{AC}}=\frac{{BE}}{{EC}}.\: \\ $$$${Take}\:{BD}=\frac{{k}}{{k}+\mathrm{1}}{BC}\:{and}\:\frac{{BE}}{{BE}−{BC}}={k};{BE}=\frac{{k}}{{k}−\mathrm{1}}{BC} \\ $$$${Then}\:{AD}\:{and}\:{AE}\:{are}\:{internal}\:{and}\:{external} \\ $$$${bisectors}\:{of}\:\angle{ABC}\Rightarrow\angle{DAE}=\mathrm{90}°\left(\mathrm{2}\alpha+\mathrm{2}\beta=\mathrm{180}°\right. \\ $$$$\left.\Rightarrow\alpha+\beta=\mathrm{90}°\right)\:{and}\:{point}\:{A}\:{lies}\:{on}\:{circle}\:{with}\: \\ $$$${diameter}\:{ED}. \\ $$$${ED}={DC}+{EC}={a}−\frac{{ak}}{{k}+\mathrm{1}}+\frac{{ak}}{{k}−\mathrm{1}}−{a} \\ $$$$={a}\left(\frac{{k}}{{k}−\mathrm{1}}−\frac{{k}}{{k}+\mathrm{1}}\right)=\left(\frac{\mathrm{2}{ak}}{{k}^{\mathrm{2}} −\mathrm{1}}\right)\Rightarrow{r}=\mid\frac{{ak}}{{k}^{\mathrm{2}} −\mathrm{1}}\mid \\ $$
