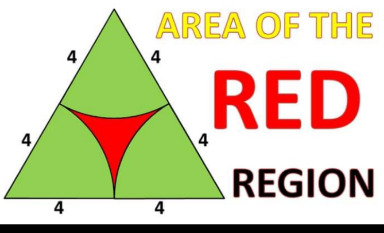
Question Number 181808 by mathocean1 last updated on 30/Nov/22
Commented by CElcedricjunior last updated on 01/Dec/22

$$\boldsymbol{{A}}_{\boldsymbol{{t}}} =\boldsymbol{{A}}_{{red}} +{A}_{{bleu}} =>{A}_{{red}} ={A}_{\boldsymbol{{t}}} −\boldsymbol{{A}}_{{bleu}} \\ $$$${or}\:{A}_{{t}} =\frac{\boldsymbol{{BH}}}{\mathrm{2}}=\frac{\mathrm{8}×\sqrt{\mathrm{8}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{8}×\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{16}\sqrt{\mathrm{3}} \\ $$$${A}_{\boldsymbol{{bleu}}} =\mathrm{3}\left(\frac{\mathrm{4}^{\mathrm{2}} \boldsymbol{\pi}}{\mathrm{6}}\right)=\frac{\mathrm{4}^{\mathrm{2}} \boldsymbol{\pi}}{\mathrm{2}}=\frac{\mathrm{16}\boldsymbol{\pi}}{\mathrm{2}}=\mathrm{8}\boldsymbol{\pi} \\ $$$$\boldsymbol{{A}}_{{red}} =\mathrm{16}\sqrt{\mathrm{3}}−\mathrm{8}\boldsymbol{\pi}\approx\mathrm{2}.\mathrm{5800}\:{um} \\ $$$$======================= \\ $$$$……{le}\:{celebre}\:{cedric}\:{junior}………… \\ $$$$=====================.=. \\ $$$$ \\ $$$$ \\ $$
Answered by BaliramKumar last updated on 30/Nov/22
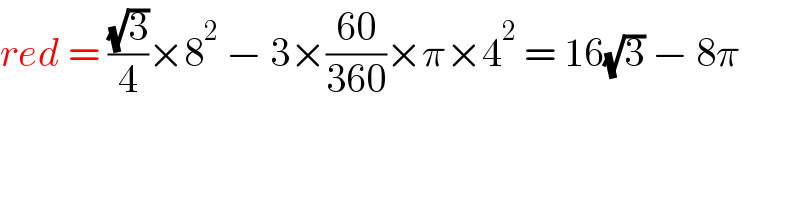
$${red}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}×\mathrm{8}^{\mathrm{2}} \:−\:\mathrm{3}×\frac{\mathrm{60}}{\mathrm{360}}×\pi×\mathrm{4}^{\mathrm{2}} \:=\:\mathrm{16}\sqrt{\mathrm{3}}\:−\:\mathrm{8}\pi \\ $$
Answered by HeferH last updated on 30/Nov/22

$$\mathrm{8}\left(\mathrm{2}\sqrt{\mathrm{3}}\:−\:\pi\right) \\ $$
Answered by a.lgnaoui last updated on 01/Dec/22
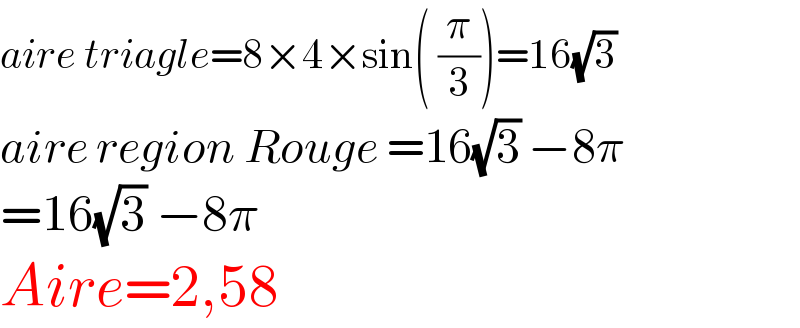
$${aire}\:{triagle}=\mathrm{8}×\mathrm{4}×\mathrm{sin}\left(\:\frac{\pi}{\mathrm{3}}\right)=\mathrm{16}\sqrt{\mathrm{3}} \\ $$$${aire}\:{region}\:{Rouge}\:=\mathrm{16}\sqrt{\mathrm{3}}\:−\mathrm{8}\pi \\ $$$$=\mathrm{16}\sqrt{\mathrm{3}}\:−\mathrm{8}\pi \\ $$$${Aire}=\mathrm{2},\mathrm{58} \\ $$
