Question-181812

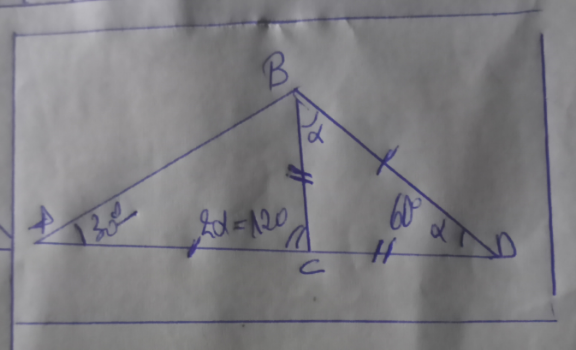
Question Number 181812 by HeferH last updated on 01/Dec/22

Answered by mr W last updated on 01/Dec/22

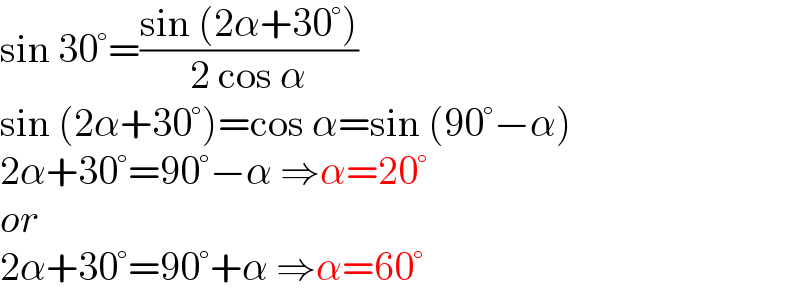
sin 30°=((sin (2α+30°))/(2 cos α)) sin (2α+30°)=cos α=sin (90°−α) 2α+30°=90°−α ⇒α=20° or 2α+30°=90°+α ⇒α=60°

$$\mathrm{sin}\:\mathrm{30}°=\frac{\mathrm{sin}\:\left(\mathrm{2}\alpha+\mathrm{30}°\right)}{\mathrm{2}\:\mathrm{cos}\:\alpha} \\ $$$$\mathrm{sin}\:\left(\mathrm{2}\alpha+\mathrm{30}°\right)=\mathrm{cos}\:\alpha=\mathrm{sin}\:\left(\mathrm{90}°−\alpha\right) \\ $$$$\mathrm{2}\alpha+\mathrm{30}°=\mathrm{90}°−\alpha\:\Rightarrow\alpha=\mathrm{20}° \\ $$$${or} \\ $$$$\mathrm{2}\alpha+\mathrm{30}°=\mathrm{90}°+\alpha\:\Rightarrow\alpha=\mathrm{60}° \\ $$

Commented by mr W last updated on 01/Dec/22

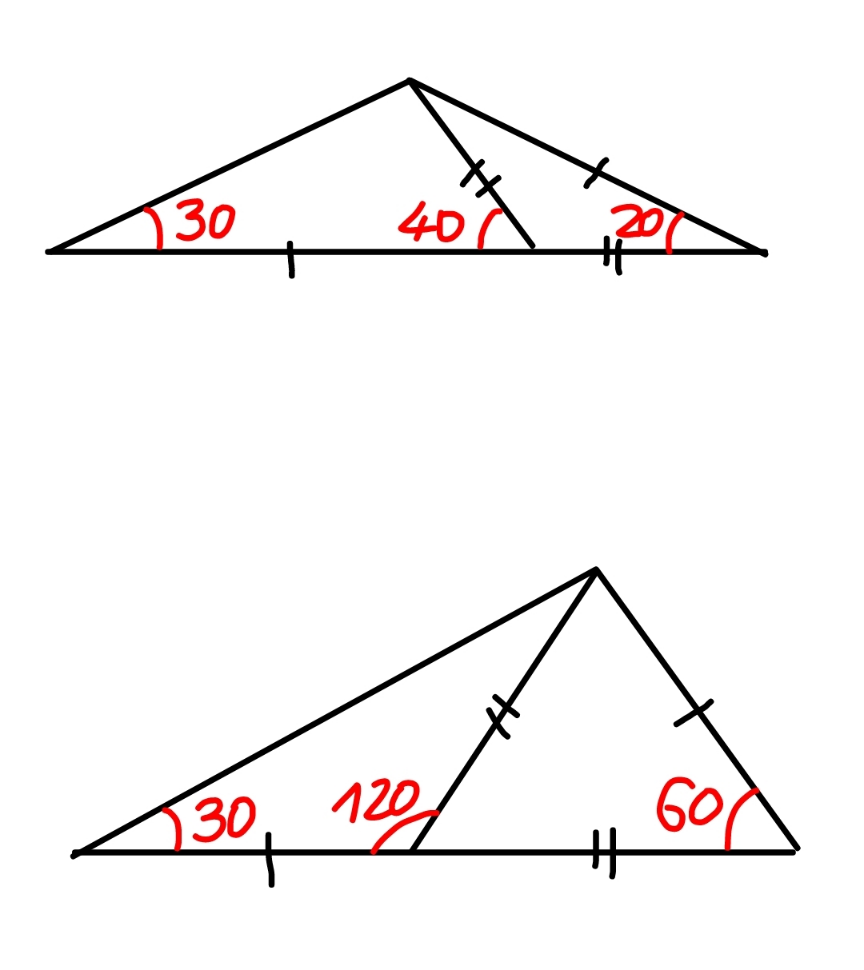
Commented by mr W last updated on 01/Dec/22

Answered by som(math1967) last updated on 01/Dec/22

let AD=DC=x,AC=BD=y from△ADC (x/(sinα))=(y/(sin(180−2α))) ⇒x=((ysinα)/(sin2α))=(y/(2cosα)) [sin2α=2sinαcosα] from△ABD (x/(sin30))=(y/(sin(180−30−2α))) ⇒(y/(2sin30cosα))=(y/(sin(150−2α))) ⇒(1/(cosα))=(1/(sin(150−2α))) ⇒sin(90−α)=sin(150−2α) ⇒90−α=150−2α ⇒2α−α=150−90 ∴ α=60 or sin(90+α)=sin(150−2α) 90+α=150−2α ⇒3α=60 ∴α=20

$${let}\:{AD}={DC}={x},{AC}={BD}={y} \\ $$$${from}\bigtriangleup{ADC}\:\:\frac{{x}}{{sin}\alpha}=\frac{{y}}{{sin}\left(\mathrm{180}−\mathrm{2}\alpha\right)} \\ $$$$\:\Rightarrow{x}=\frac{{ysin}\alpha}{{sin}\mathrm{2}\alpha}=\frac{{y}}{\mathrm{2}{cos}\alpha}\:\:\left[{sin}\mathrm{2}\alpha=\mathrm{2}{sin}\alpha{cos}\alpha\right] \\ $$$${from}\bigtriangleup{ABD}\: \\ $$$$\:\:\frac{{x}}{{sin}\mathrm{30}}=\frac{{y}}{{sin}\left(\mathrm{180}−\mathrm{30}−\mathrm{2}\alpha\right)} \\ $$$$\Rightarrow\frac{{y}}{\mathrm{2}{sin}\mathrm{30}{cos}\alpha}=\frac{{y}}{{sin}\left(\mathrm{150}−\mathrm{2}\alpha\right)} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{cos}\alpha}=\frac{\mathrm{1}}{{sin}\left(\mathrm{150}−\mathrm{2}\alpha\right)} \\ $$$$\Rightarrow{sin}\left(\mathrm{90}−\alpha\right)={sin}\left(\mathrm{150}−\mathrm{2}\alpha\right) \\ $$$$\Rightarrow\mathrm{90}−\alpha=\mathrm{150}−\mathrm{2}\alpha \\ $$$$\Rightarrow\mathrm{2}\alpha−\alpha=\mathrm{150}−\mathrm{90} \\ $$$$\therefore\:\alpha=\mathrm{60} \\ $$$${or} \\ $$$${sin}\left(\mathrm{90}+\alpha\right)={sin}\left(\mathrm{150}−\mathrm{2}\alpha\right) \\ $$$$\:\mathrm{90}+\alpha=\mathrm{150}−\mathrm{2}\alpha \\ $$$$\Rightarrow\mathrm{3}\alpha=\mathrm{60}\:\therefore\alpha=\mathrm{20} \\ $$

Commented by som(math1967) last updated on 01/Dec/22

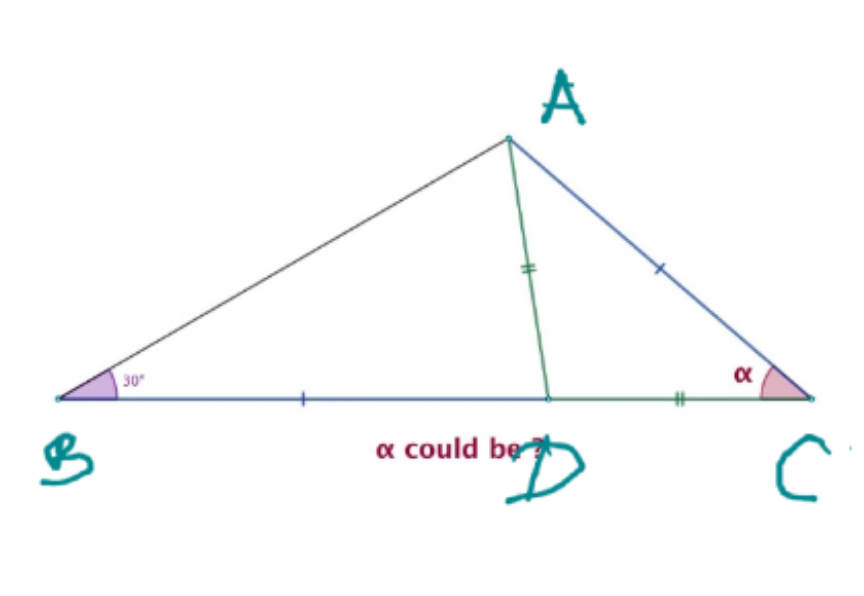
Answered by Acem last updated on 01/Dec/22

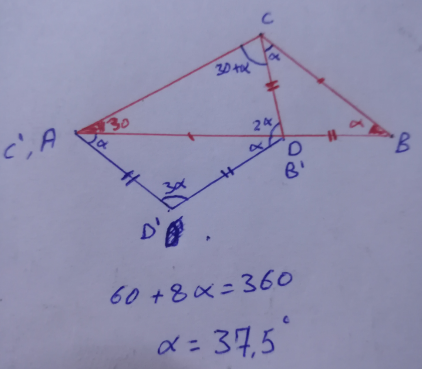
Commented by Acem last updated on 01/Dec/22

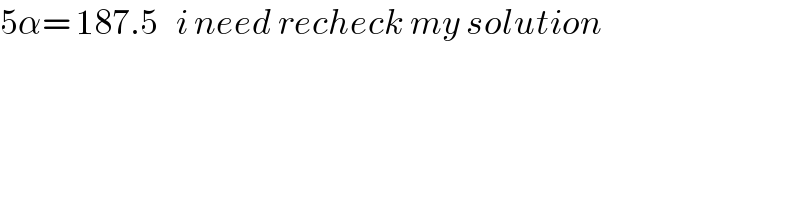
$$\mathrm{5}\alpha=\:\mathrm{187}.\mathrm{5}\:\:\:{i}\:{need}\:{recheck}\:{my}\:{solution} \\ $$

Answered by HeferH last updated on 01/Dec/22

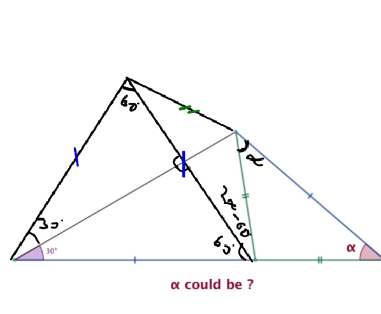
Commented by HeferH last updated on 01/Dec/22

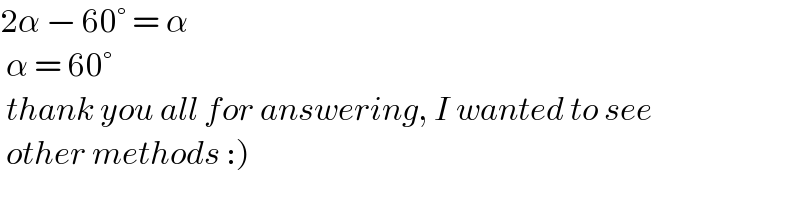
2α − 60° = α α = 60° thank you all for answering, I wanted to see other methods :)

$$\mathrm{2}\alpha\:−\:\mathrm{60}°\:=\:\alpha\: \\ $$$$\:\alpha\:=\:\mathrm{60}° \\ $$$$\:{thank}\:{you}\:{all}\:{for}\:{answering},\:{I}\:{wanted}\:{to}\:{see} \\ $$$$\left.\:{other}\:{methods}\::\right) \\ $$

Answered by a.lgnaoui last updated on 01/Dec/22

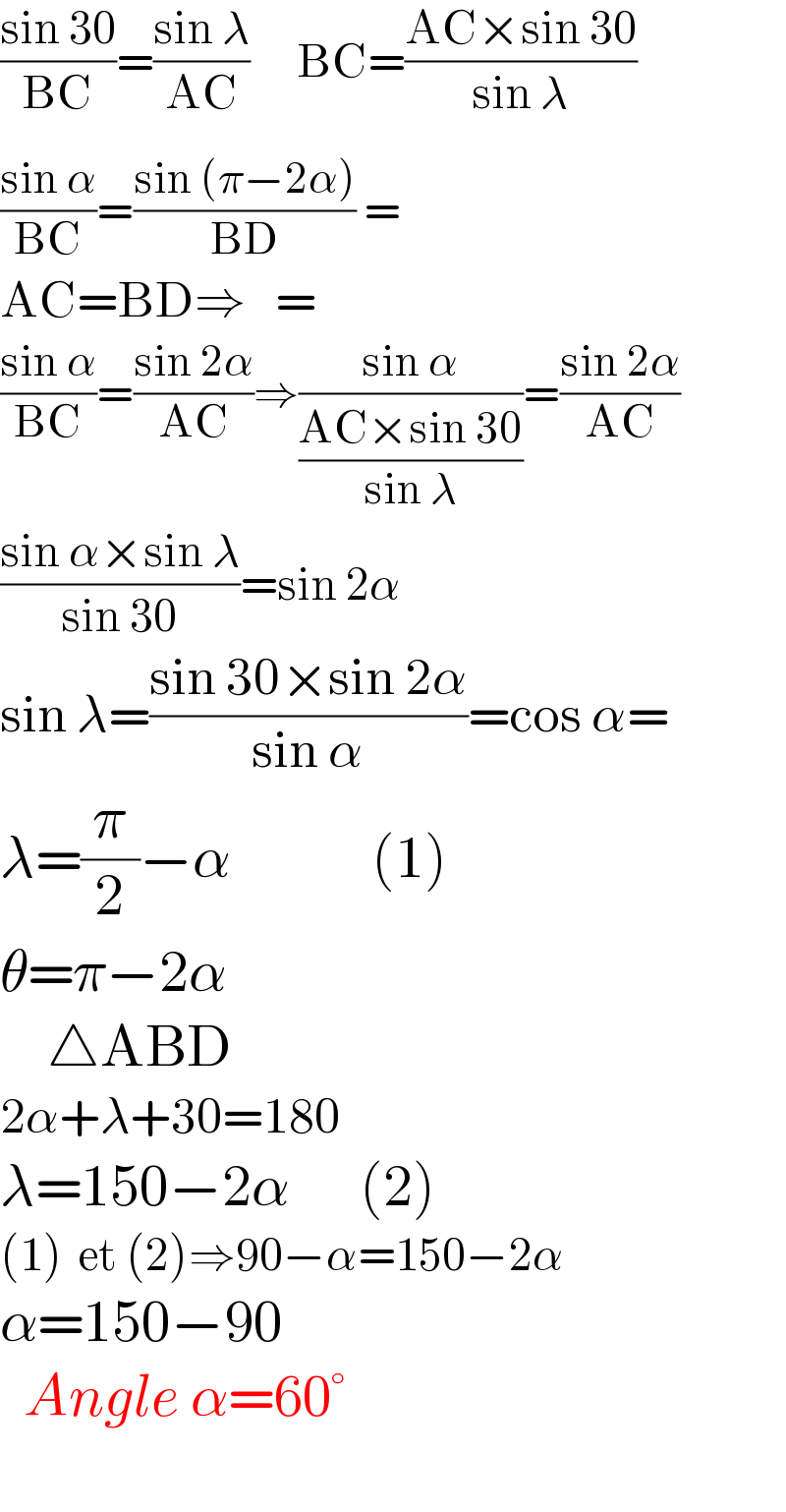
((sin 30)/(BC))=((sin λ)/(AC)) BC=((AC×sin 30)/(sin λ)) ((sin α)/(BC))=((sin (π−2α)^ )/(BD)) = AC=BD⇒ = ((sin α)/(BC))=((sin 2α)/(AC))⇒((sin α)/((AC×sin 30)/(sin λ)))=((sin 2α)/(AC)) ((sin α×sin λ)/(sin 30))=sin 2α sin λ=((sin 30×sin 2α)/(sin α))=cos α= λ=(π/2)−α (1) θ=π−2α △ABD 2α+λ+30=180 λ=150−2α (2) (1) et (2)⇒90−α=150−2α α=150−90 Angle α=60°

$$\frac{\mathrm{sin}\:\mathrm{30}}{\mathrm{BC}}=\frac{\mathrm{sin}\:\lambda}{\mathrm{AC}}\:\:\:\:\:\:\mathrm{BC}=\frac{\mathrm{AC}×\mathrm{sin}\:\mathrm{30}}{\mathrm{sin}\:\lambda} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{BC}}=\frac{\mathrm{sin}\:\left(\pi−\mathrm{2}\alpha\overset{} {\right)}}{\mathrm{BD}}\:= \\ $$$$\mathrm{AC}=\mathrm{BD}\Rightarrow\:\:\:= \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{BC}}=\frac{\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{AC}}\Rightarrow\frac{\mathrm{sin}\:\alpha}{\frac{\mathrm{AC}×\mathrm{sin}\:\mathrm{30}}{\mathrm{sin}\:\lambda}}=\frac{\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{AC}} \\ $$$$\frac{\mathrm{sin}\:\alpha×\mathrm{sin}\:\lambda}{\mathrm{sin}\:\mathrm{30}}=\mathrm{sin}\:\mathrm{2}\alpha \\ $$$$\mathrm{sin}\:\lambda=\frac{\mathrm{sin}\:\mathrm{30}×\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{sin}\:\alpha}=\mathrm{cos}\:\alpha= \\ $$$$\lambda=\frac{\pi}{\mathrm{2}}−\alpha\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\theta=\pi−\mathrm{2}\alpha \\ $$$$\:\:\:\:\bigtriangleup\mathrm{ABD}\:\:\: \\ $$$$\mathrm{2}\alpha+\lambda+\mathrm{30}=\mathrm{180} \\ $$$$\lambda=\mathrm{150}−\mathrm{2}\alpha\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{et}\:\left(\mathrm{2}\right)\Rightarrow\mathrm{90}−\alpha=\mathrm{150}−\mathrm{2}\alpha \\ $$$$\alpha=\mathrm{150}−\mathrm{90} \\ $$$$\:\:{Angle}\:\alpha=\mathrm{60}° \\ $$$$ \\ $$

Commented by a.lgnaoui last updated on 01/Dec/22

Facebook Tweet Pin

Leave a Reply Cancel reply