Menu Close

Question-181858

Tinku Tara 0 Comments
Pin




Question Number 181858 by KINMATICS last updated on 01/Dec/22
Answered by hmr last updated on 01/Dec/22
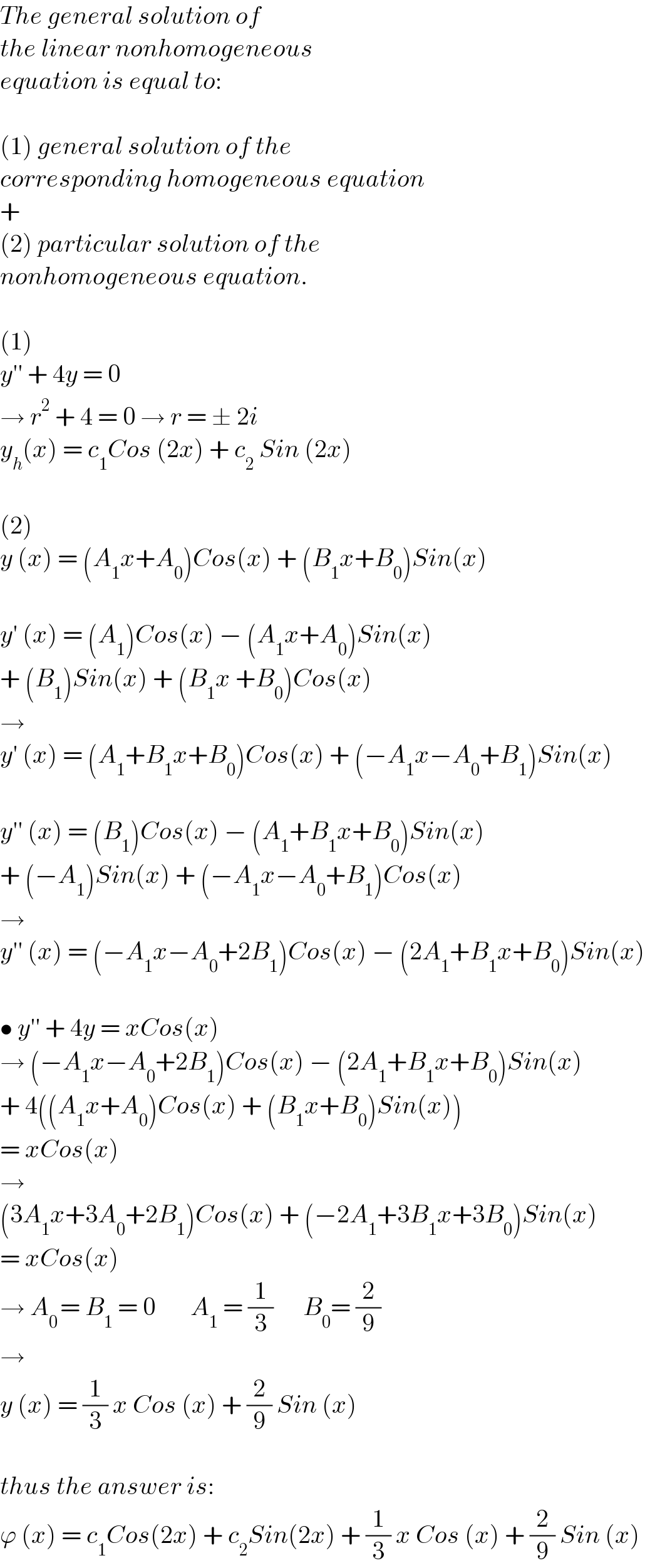
The general solution of the linear nonhomogeneous equation is equal to: (1) general solution of the corresponding homogeneous equation + (2) particular solution of the nonhomogeneous equation. (1) y′′ + 4y = 0 → r^2 + 4 = 0 → r = ± 2i y_h (x) = c_1 Cos (2x) + c_2 Sin (2x) (2) y (x) = (A_1 x+A_0 )Cos(x) + (B_1 x+B_0 )Sin(x) y′ (x) = (A_1 )Cos(x) − (A_1 x+A_0 )Sin(x) + (B_1 )Sin(x) + (B_1 x +B_0 )Cos(x) → y′ (x) = (A_1 +B_1 x+B_0 )Cos(x) + (−A_1 x−A_0 +B_1 )Sin(x) y′′ (x) = (B_1 )Cos(x) − (A_1 +B_1 x+B_0 )Sin(x) + (−A_1 )Sin(x) + (−A_1 x−A_0 +B_1 )Cos(x) → y′′ (x) = (−A_1 x−A_0 +2B_1 )Cos(x) − (2A_1 +B_1 x+B_0 )Sin(x) • y′′ + 4y = xCos(x) → (−A_1 x−A_0 +2B_1 )Cos(x) − (2A_1 +B_1 x+B_0 )Sin(x) + 4((A_1 x+A_0 )Cos(x) + (B_1 x+B_0 )Sin(x)) = xCos(x) → (3A_1 x+3A_0 +2B_1 )Cos(x) + (−2A_1 +3B_1 x+3B_0 )Sin(x) = xCos(x) → A_(0 ) = B_1 = 0 A_1 = (1/3) B_0 = (2/9) → y (x) = (1/3) x Cos (x) + (2/9) Sin (x) thus the answer is: ϕ (x) = c_1 Cos(2x) + c_2 Sin(2x) + (1/3) x Cos (x) + (2/9) Sin (x)
$${The}\:{general}\:{solution}\:{of} \\ $$$${the}\:{linear}\:{nonhomogeneous} \\ $$$${equation}\:{is}\:{equal}\:{to}: \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{general}\:{solution}\:{of}\:{the} \\ $$$${corresponding}\:{homogeneous}\:{equation} \\ $$$$+ \\ $$$$\left(\mathrm{2}\right)\:{particular}\:{solution}\:{of}\:{the} \\ $$$${nonhomogeneous}\:{equation}. \\ $$$$ \\ $$$$\left(\mathrm{1}\right) \\ $$$${y}''\:+\:\mathrm{4}{y}\:=\:\mathrm{0} \\ $$$$\rightarrow\:{r}^{\mathrm{2}} \:+\:\mathrm{4}\:=\:\mathrm{0}\:\rightarrow\:{r}\:=\:\pm\:\mathrm{2}{i} \\ $$$${y}_{{h}} \left({x}\right)\:=\:{c}_{\mathrm{1}} {Cos}\:\left(\mathrm{2}{x}\right)\:+\:{c}_{\mathrm{2}} \:{Sin}\:\left(\mathrm{2}{x}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${y}\:\left({x}\right)\:=\:\left({A}_{\mathrm{1}} {x}+{A}_{\mathrm{0}} \right){Cos}\left({x}\right)\:+\:\left({B}_{\mathrm{1}} {x}+{B}_{\mathrm{0}} \right){Sin}\left({x}\right) \\ $$$$ \\ $$$${y}'\:\left({x}\right)\:=\:\left({A}_{\mathrm{1}} \right){Cos}\left({x}\right)\:−\:\left({A}_{\mathrm{1}} {x}+{A}_{\mathrm{0}} \right){Sin}\left({x}\right) \\ $$$$+\:\left({B}_{\mathrm{1}} \right){Sin}\left({x}\right)\:+\:\left({B}_{\mathrm{1}} {x}\:+{B}_{\mathrm{0}} \right){Cos}\left({x}\right) \\ $$$$\rightarrow\: \\ $$$${y}'\:\left({x}\right)\:=\:\left({A}_{\mathrm{1}} +{B}_{\mathrm{1}} {x}+{B}_{\mathrm{0}} \right){Cos}\left({x}\right)\:+\:\left(−{A}_{\mathrm{1}} {x}−{A}_{\mathrm{0}} +{B}_{\mathrm{1}} \right){Sin}\left({x}\right) \\ $$$$ \\ $$$${y}''\:\left({x}\right)\:=\:\left({B}_{\mathrm{1}} \right){Cos}\left({x}\right)\:−\:\left({A}_{\mathrm{1}} +{B}_{\mathrm{1}} {x}+{B}_{\mathrm{0}} \right){Sin}\left({x}\right) \\ $$$$+\:\left(−{A}_{\mathrm{1}} \right){Sin}\left({x}\right)\:+\:\left(−{A}_{\mathrm{1}} {x}−{A}_{\mathrm{0}} +{B}_{\mathrm{1}} \right){Cos}\left({x}\right) \\ $$$$\rightarrow \\ $$$${y}''\:\left({x}\right)\:=\:\left(−{A}_{\mathrm{1}} {x}−{A}_{\mathrm{0}} +\mathrm{2}{B}_{\mathrm{1}} \right){Cos}\left({x}\right)\:−\:\left(\mathrm{2}{A}_{\mathrm{1}} +{B}_{\mathrm{1}} {x}+{B}_{\mathrm{0}} \right){Sin}\left({x}\right) \\ $$$$ \\ $$$$\bullet\:{y}''\:+\:\mathrm{4}{y}\:=\:{xCos}\left({x}\right) \\ $$$$\rightarrow\:\left(−{A}_{\mathrm{1}} {x}−{A}_{\mathrm{0}} +\mathrm{2}{B}_{\mathrm{1}} \right){Cos}\left({x}\right)\:−\:\left(\mathrm{2}{A}_{\mathrm{1}} +{B}_{\mathrm{1}} {x}+{B}_{\mathrm{0}} \right){Sin}\left({x}\right) \\ $$$$+\:\mathrm{4}\left(\left({A}_{\mathrm{1}} {x}+{A}_{\mathrm{0}} \right){Cos}\left({x}\right)\:+\:\left({B}_{\mathrm{1}} {x}+{B}_{\mathrm{0}} \right){Sin}\left({x}\right)\right) \\ $$$$=\:{xCos}\left({x}\right) \\ $$$$\rightarrow \\ $$$$\left(\mathrm{3}{A}_{\mathrm{1}} {x}+\mathrm{3}{A}_{\mathrm{0}} +\mathrm{2}{B}_{\mathrm{1}} \right){Cos}\left({x}\right)\:+\:\left(−\mathrm{2}{A}_{\mathrm{1}} +\mathrm{3}{B}_{\mathrm{1}} {x}+\mathrm{3}{B}_{\mathrm{0}} \right){Sin}\left({x}\right) \\ $$$$=\:{xCos}\left({x}\right) \\ $$$$\rightarrow\:{A}_{\mathrm{0}\:} =\:{B}_{\mathrm{1}} \:=\:\mathrm{0}\:\:\:\:\:\:\:{A}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:{B}_{\mathrm{0}} =\:\frac{\mathrm{2}}{\mathrm{9}} \\ $$$$\rightarrow \\ $$$${y}\:\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:{x}\:{Cos}\:\left({x}\right)\:+\:\frac{\mathrm{2}}{\mathrm{9}}\:{Sin}\:\left({x}\right) \\ $$$$ \\ $$$${thus}\:{the}\:{answer}\:{is}: \\ $$$$\varphi\:\left({x}\right)\:=\:{c}_{\mathrm{1}} {Cos}\left(\mathrm{2}{x}\right)\:+\:{c}_{\mathrm{2}} {Sin}\left(\mathrm{2}{x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\:{x}\:{Cos}\:\left({x}\right)\:+\:\frac{\mathrm{2}}{\mathrm{9}}\:{Sin}\:\left({x}\right) \\ $$
Commented by hmr last updated on 01/Dec/22
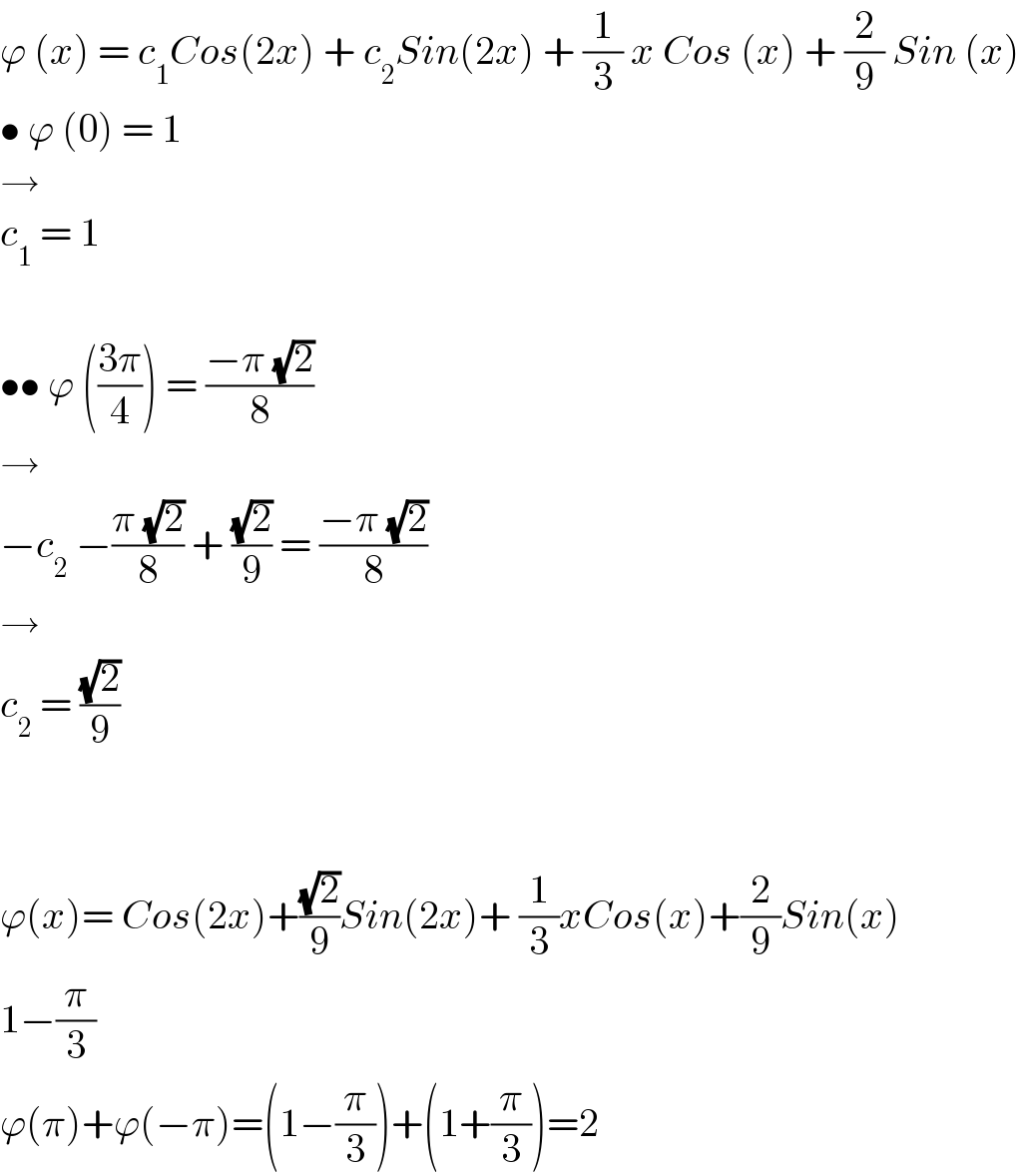
ϕ (x) = c_1 Cos(2x) + c_2 Sin(2x) + (1/3) x Cos (x) + (2/9) Sin (x) • ϕ (0) = 1 → c_1 = 1 •• ϕ (((3π)/4)) = ((−π (√2))/8) → −c_2 −((π (√2))/8) + ((√2)/9) = ((−π (√2))/8) → c_2 = ((√2)/9) ϕ(x)= Cos(2x)+((√2)/9)Sin(2x)+ (1/3)xCos(x)+(2/9)Sin(x) 1−(π/3) ϕ(π)+ϕ(−π)=(1−(π/3))+(1+(π/3))=2
$$\varphi\:\left({x}\right)\:=\:{c}_{\mathrm{1}} {Cos}\left(\mathrm{2}{x}\right)\:+\:{c}_{\mathrm{2}} {Sin}\left(\mathrm{2}{x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\:{x}\:{Cos}\:\left({x}\right)\:+\:\frac{\mathrm{2}}{\mathrm{9}}\:{Sin}\:\left({x}\right) \\ $$$$\bullet\:\varphi\:\left(\mathrm{0}\right)\:=\:\mathrm{1} \\ $$$$\rightarrow \\ $$$${c}_{\mathrm{1}} \:=\:\mathrm{1} \\ $$$$ \\ $$$$\bullet\bullet\:\varphi\:\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\:=\:\frac{−\pi\:\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\rightarrow \\ $$$$−{c}_{\mathrm{2}} \:−\frac{\pi\:\sqrt{\mathrm{2}}}{\mathrm{8}}\:+\:\frac{\sqrt{\mathrm{2}}}{\mathrm{9}}\:=\:\frac{−\pi\:\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\rightarrow \\ $$$${c}_{\mathrm{2}} \:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{9}} \\ $$$$ \\ $$$$ \\ $$$$\varphi\left({x}\right)=\:{Cos}\left(\mathrm{2}{x}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{9}}{Sin}\left(\mathrm{2}{x}\right)+\:\frac{\mathrm{1}}{\mathrm{3}}{xCos}\left({x}\right)+\frac{\mathrm{2}}{\mathrm{9}}{Sin}\left({x}\right) \\ $$$$\mathrm{1}−\frac{\pi}{\mathrm{3}} \\ $$$$\varphi\left(\pi\right)+\varphi\left(−\pi\right)=\left(\mathrm{1}−\frac{\pi}{\mathrm{3}}\right)+\left(\mathrm{1}+\frac{\pi}{\mathrm{3}}\right)=\mathrm{2} \\ $$
Answered by qaz last updated on 01/Dec/22
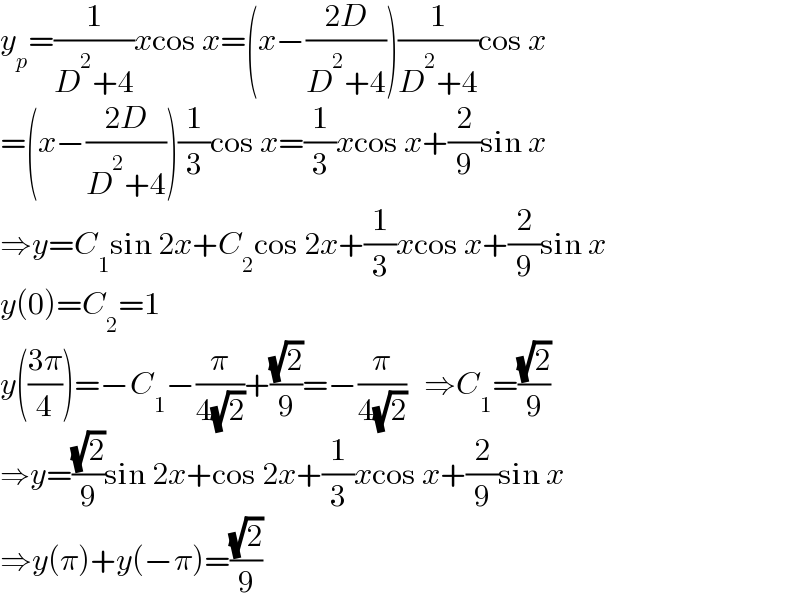
y_p =(1/(D^2 +4))xcos x=(x−((2D)/(D^2 +4)))(1/(D^2 +4))cos x =(x−((2D)/(D^2 +4)))(1/3)cos x=(1/3)xcos x+(2/9)sin x ⇒y=C_1 sin 2x+C_2 cos 2x+(1/3)xcos x+(2/9)sin x y(0)=C_2 =1 y(((3π)/4))=−C_1 −(π/(4(√2)))+((√2)/9)=−(π/(4(√2))) ⇒C_1 =((√2)/9) ⇒y=((√2)/9)sin 2x+cos 2x+(1/3)xcos x+(2/9)sin x ⇒y(π)+y(−π)=((√2)/9)
$${y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{4}}{x}\mathrm{cos}\:{x}=\left({x}−\frac{\mathrm{2}{D}}{{D}^{\mathrm{2}} +\mathrm{4}}\right)\frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{4}}\mathrm{cos}\:{x} \\ $$$$=\left({x}−\frac{\mathrm{2}{D}}{{D}^{\mathrm{2}} +\mathrm{4}}\right)\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{3}}{x}\mathrm{cos}\:{x}+\frac{\mathrm{2}}{\mathrm{9}}\mathrm{sin}\:{x} \\ $$$$\Rightarrow{y}={C}_{\mathrm{1}} \mathrm{sin}\:\mathrm{2}{x}+{C}_{\mathrm{2}} \mathrm{cos}\:\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{3}}{x}\mathrm{cos}\:{x}+\frac{\mathrm{2}}{\mathrm{9}}\mathrm{sin}\:{x} \\ $$$${y}\left(\mathrm{0}\right)={C}_{\mathrm{2}} =\mathrm{1} \\ $$$${y}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)=−{C}_{\mathrm{1}} −\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{9}}=−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\:\:\Rightarrow{C}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{9}} \\ $$$$\Rightarrow{y}=\frac{\sqrt{\mathrm{2}}}{\mathrm{9}}\mathrm{sin}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{3}}{x}\mathrm{cos}\:{x}+\frac{\mathrm{2}}{\mathrm{9}}\mathrm{sin}\:{x} \\ $$$$\Rightarrow{y}\left(\pi\right)+{y}\left(−\pi\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{9}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *