Question Number 181897 by Acem last updated on 01/Dec/22

Answered by mr W last updated on 02/Dec/22
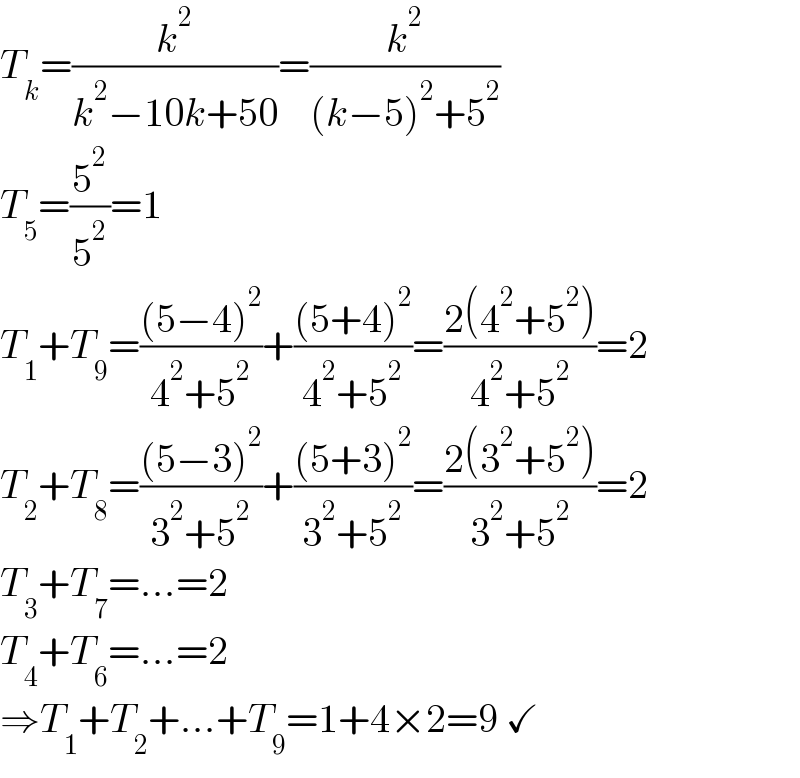
$${T}_{{k}} =\frac{{k}^{\mathrm{2}} }{{k}^{\mathrm{2}} −\mathrm{10}{k}+\mathrm{50}}=\frac{{k}^{\mathrm{2}} }{\left({k}−\mathrm{5}\right)^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} } \\ $$$${T}_{\mathrm{5}} =\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{5}^{\mathrm{2}} }=\mathrm{1} \\ $$$${T}_{\mathrm{1}} +{T}_{\mathrm{9}} =\frac{\left(\mathrm{5}−\mathrm{4}\right)^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }+\frac{\left(\mathrm{5}+\mathrm{4}\right)^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }=\frac{\mathrm{2}\left(\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \right)}{\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }=\mathrm{2} \\ $$$${T}_{\mathrm{2}} +{T}_{\mathrm{8}} =\frac{\left(\mathrm{5}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }+\frac{\left(\mathrm{5}+\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }=\frac{\mathrm{2}\left(\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \right)}{\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }=\mathrm{2} \\ $$$${T}_{\mathrm{3}} +{T}_{\mathrm{7}} =…=\mathrm{2} \\ $$$${T}_{\mathrm{4}} +{T}_{\mathrm{6}} =…=\mathrm{2} \\ $$$$\Rightarrow{T}_{\mathrm{1}} +{T}_{\mathrm{2}} +…+{T}_{\mathrm{9}} =\mathrm{1}+\mathrm{4}×\mathrm{2}=\mathrm{9}\:\checkmark \\ $$
Commented by Acem last updated on 02/Dec/22

$${Very}\:{well}!\:{Thanks} \\ $$
Answered by Acem last updated on 02/Dec/22
![(1^2 /(1^2 −10+50))= ((2.1^2 )/(1^2 +1−20+100))= ((2.1^2 )/(1^2 + (10−1)^2 )) ...i (9^2 /(9^2 −90+50))= ((2 (10−1)^2 )/((10−1)^2 +(10−1)^2 −20(10−1)+100)) = ((2 (10−1)^2 )/((10−1)^2 +[10−(10−1)]^2 ))= ((2 (10−1)^2 )/(1^2 +(10−1)^2 )) ...ii i+ii = ((2 [1+(10−1)^2 ])/(1+(10−1)^2 ))= 2 Then ((2n^2 )/(n^2 +(10−n)^2 ))+ ((2 (10−n)^2 )/(n^2 +(10−n)^2 ))= 2 ∀n∈ N, n> 0 we have n= 9 : n=1 to 9 ; Terms= {1, 2, ..., 9} Sum= 4×2_(1,9& 2,8,...) + T_5 = 9 ; T_5 = 1](https://www.tinkutara.com/question/Q181941.png)
$$\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}^{\mathrm{2}} −\mathrm{10}+\mathrm{50}}=\:\frac{\mathrm{2}.\mathrm{1}^{\mathrm{2}} }{\mathrm{1}^{\mathrm{2}} +\mathrm{1}−\mathrm{20}+\mathrm{100}}=\:\:\frac{\mathrm{2}.\mathrm{1}^{\mathrm{2}} }{\mathrm{1}^{\mathrm{2}} +\:\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} }\:…{i} \\ $$$$\frac{\mathrm{9}^{\mathrm{2}} }{\mathrm{9}^{\mathrm{2}} −\mathrm{90}+\mathrm{50}}=\:\frac{\mathrm{2}\:\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{20}\left(\mathrm{10}−\mathrm{1}\right)+\mathrm{100}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}\:\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} +\left[\mathrm{10}−\left(\mathrm{10}−\mathrm{1}\right)\right]^{\mathrm{2}} }=\:\frac{\mathrm{2}\:\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{1}^{\mathrm{2}} +\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} }\:…{ii} \\ $$$$ \\ $$$$\:{i}+{ii}\:=\:\frac{\mathrm{2}\:\left[\mathrm{1}+\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} \right]}{\mathrm{1}+\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{2}} }=\:\mathrm{2} \\ $$$$\:{Then}\:\frac{\mathrm{2}{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} +\left(\mathrm{10}−{n}\right)^{\mathrm{2}} }+\:\frac{\mathrm{2}\:\left(\mathrm{10}−{n}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} +\left(\mathrm{10}−{n}\right)^{\mathrm{2}} }=\:\mathrm{2}\:\forall{n}\in\:\mathbb{N},\:{n}>\:\mathrm{0} \\ $$$$ \\ $$$$\:{we}\:{have}\:{n}=\:\mathrm{9}\::\:{n}=\mathrm{1}\:{to}\:\mathrm{9}\:;\:{Terms}=\:\left\{\mathrm{1},\:\mathrm{2},\:…,\:\mathrm{9}\right\} \\ $$$$\:{Sum}=\:\mathrm{4}×\mathrm{2}_{\mathrm{1},\mathrm{9\&}\:\mathrm{2},\mathrm{8},…} +\:{T}_{\mathrm{5}} =\:\mathrm{9}\:;\:{T}_{\mathrm{5}} =\:\mathrm{1} \\ $$$$ \\ $$
