Question Number 181902 by Acem last updated on 01/Dec/22

Answered by Rasheed.Sindhi last updated on 02/Dec/22
![(x^2 +xy+y^2 )(√(x^2 +y^2 )) =185....(i) (x^2 −xy+y^2 )(√(x^2 +y^2 )) =65.....(ii) [(√(x^2 +y^2 )) ≠0] (i)/(ii): ((x^2 +xy+y^2 )/(x^2 −xy+y^2 ))=((185)/(65))=((37)/(13)) ((x^2 +xy+y^2 −x^2 +xy−y^2 )/(x^2 +xy+y^2 +x^2 −xy+y^2 ))=((37−13)/(37+13)) [Componendo-Dividendo property] ((2xy)/(2x^2 +2y^2 ))=((37−13)/(37+13)) ((xy)/(x^2 +y^2 ))=((12)/(25)) 12x^2 −25xy+12y^2 =0 ((12x)/(25y))+((12y)/(25x))=1 ((12)/(25))(t+(1/t))=1 t+(1/t)=((25)/(12)) 12t^2 −25t+12=0 t=((25±(√(625−576)))/(24))=((25±7)/(24))=(4/3),(3/4) (x/y)=(4/3),(3/4) 3x=4y ∨ 4x=3y y=((3x)/4),((4x)/3) y=((3x)/4): (i)⇒( x^2 +x(((3x)/4))+(((3x)/4))^2 )(√(x^2 +(((3x)/4))^2 )) =185 ((16x^2 +12x^2 +9x^2 )/(16))(√((16x^2 +9x^2 )/(16))) =185 ((37x^2 )/(16))∙((5∣x∣)/4) =185 ∣x∣^3 =((185∙64)/(5∙37))=4^3 ⇒∣x∣=4⇒x=±4 ⇒y=((3(±4))/4)=±3 y=((4x)/3): (i)⇒(x^2 +x(((4x)/3))+(((4x)/3))^2 )(√(x^2 +(((4x)/3))^2 )) =185 ((9x^2 +12x^2 +16x^2 )/9)(√((9x^2 +16x^2 )/9)) =185 ((37x^2 )/9)∙((5∣x∣)/3)=185 ∣x∣^3 =((185×27)/(37×5))⇒∣x∣=3⇒x=±3 ⇒y=((4(±3))/3)=±4 (x,y)={(4,3),(3,4),(−4,−3),(−3,−4)}](https://www.tinkutara.com/question/Q181919.png)
$$\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\mathrm{185}….\left({i}\right) \\ $$$$\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\mathrm{65}…..\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\neq\mathrm{0}\right] \\ $$$$\left({i}\right)/\left({ii}\right):\:\frac{{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} }=\frac{\mathrm{185}}{\mathrm{65}}=\frac{\mathrm{37}}{\mathrm{13}} \\ $$$$\frac{{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} −{x}^{\mathrm{2}} +{xy}−{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} +{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} }=\frac{\mathrm{37}−\mathrm{13}}{\mathrm{37}+\mathrm{13}}\: \\ $$$$\:\:\:\left[{Componendo}-{Dividendo}\:{property}\right] \\ $$$$\frac{\mathrm{2}{xy}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} }=\frac{\mathrm{37}−\mathrm{13}}{\mathrm{37}+\mathrm{13}} \\ $$$$\frac{{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\frac{\mathrm{12}}{\mathrm{25}} \\ $$$$\mathrm{12}{x}^{\mathrm{2}} −\mathrm{25}{xy}+\mathrm{12}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{12}{x}}{\mathrm{25}{y}}+\frac{\mathrm{12}{y}}{\mathrm{25}{x}}=\mathrm{1} \\ $$$$\frac{\mathrm{12}}{\mathrm{25}}\left({t}+\frac{\mathrm{1}}{{t}}\right)=\mathrm{1} \\ $$$${t}+\frac{\mathrm{1}}{{t}}=\frac{\mathrm{25}}{\mathrm{12}} \\ $$$$\mathrm{12}{t}^{\mathrm{2}} −\mathrm{25}{t}+\mathrm{12}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{25}\pm\sqrt{\mathrm{625}−\mathrm{576}}}{\mathrm{24}}=\frac{\mathrm{25}\pm\mathrm{7}}{\mathrm{24}}=\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{3}{x}=\mathrm{4}{y}\:\vee\:\mathrm{4}{x}=\mathrm{3}{y} \\ $$$${y}=\frac{\mathrm{3}{x}}{\mathrm{4}},\frac{\mathrm{4}{x}}{\mathrm{3}} \\ $$$$ \\ $$$${y}=\frac{\mathrm{3}{x}}{\mathrm{4}}: \\ $$$$\left({i}\right)\Rightarrow\left(\:{x}^{\mathrm{2}} +{x}\left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right)+\left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right)^{\mathrm{2}} \:\right)\sqrt{{x}^{\mathrm{2}} +\left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right)^{\mathrm{2}} }\:=\mathrm{185} \\ $$$$\frac{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{16}}\sqrt{\frac{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{16}}}\:=\mathrm{185} \\ $$$$\frac{\mathrm{37}{x}^{\mathrm{2}} }{\mathrm{16}}\centerdot\frac{\mathrm{5}\mid{x}\mid}{\mathrm{4}}\:=\mathrm{185} \\ $$$$\mid{x}\mid^{\mathrm{3}} =\frac{\mathrm{185}\centerdot\mathrm{64}}{\mathrm{5}\centerdot\mathrm{37}}=\mathrm{4}^{\mathrm{3}} \Rightarrow\mid{x}\mid=\mathrm{4}\Rightarrow{x}=\pm\mathrm{4} \\ $$$$\Rightarrow{y}=\frac{\mathrm{3}\left(\pm\mathrm{4}\right)}{\mathrm{4}}=\pm\mathrm{3} \\ $$$${y}=\frac{\mathrm{4}{x}}{\mathrm{3}}: \\ $$$$\left({i}\right)\Rightarrow\left({x}^{\mathrm{2}} +{x}\left(\frac{\mathrm{4}{x}}{\mathrm{3}}\right)+\left(\frac{\mathrm{4}{x}}{\mathrm{3}}\right)^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +\left(\frac{\mathrm{4}{x}}{\mathrm{3}}\right)^{\mathrm{2}} }\:=\mathrm{185} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{16}{x}^{\mathrm{2}} }{\mathrm{9}}\sqrt{\frac{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{16}{x}^{\mathrm{2}} }{\mathrm{9}}}\:=\mathrm{185} \\ $$$$\:\:\:\frac{\mathrm{37}{x}^{\mathrm{2}} }{\mathrm{9}}\centerdot\frac{\mathrm{5}\mid{x}\mid}{\mathrm{3}}=\mathrm{185} \\ $$$$\:\:\:\:\mid{x}\mid^{\mathrm{3}} =\frac{\mathrm{185}×\mathrm{27}}{\mathrm{37}×\mathrm{5}}\Rightarrow\mid{x}\mid=\mathrm{3}\Rightarrow{x}=\pm\mathrm{3} \\ $$$$\Rightarrow{y}=\frac{\mathrm{4}\left(\pm\mathrm{3}\right)}{\mathrm{3}}=\pm\mathrm{4} \\ $$$$\left({x},{y}\right)=\left\{\left(\mathrm{4},\mathrm{3}\right),\left(\mathrm{3},\mathrm{4}\right),\left(−\mathrm{4},−\mathrm{3}\right),\left(−\mathrm{3},−\mathrm{4}\right)\right\} \\ $$
Answered by mr W last updated on 02/Dec/22
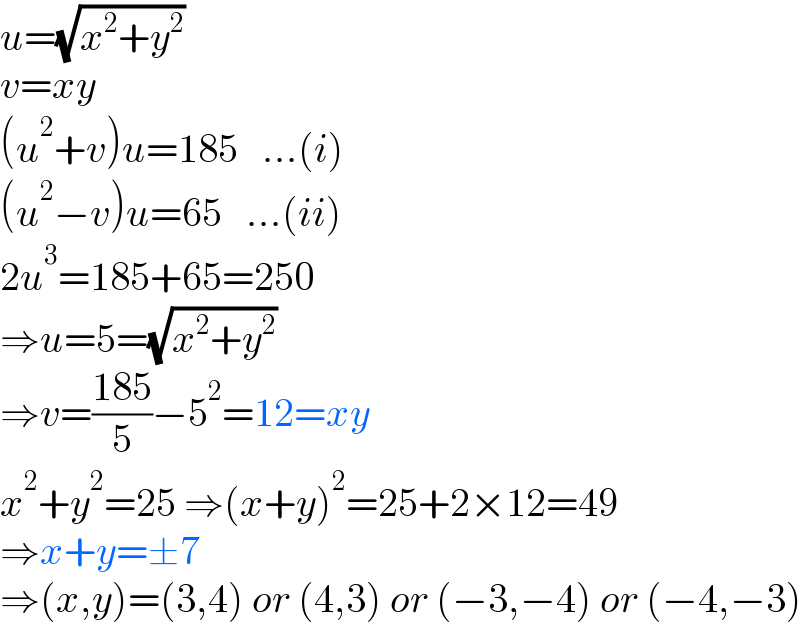
$${u}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${v}={xy} \\ $$$$\left({u}^{\mathrm{2}} +{v}\right){u}=\mathrm{185}\:\:\:…\left({i}\right) \\ $$$$\left({u}^{\mathrm{2}} −{v}\right){u}=\mathrm{65}\:\:\:…\left({ii}\right) \\ $$$$\mathrm{2}{u}^{\mathrm{3}} =\mathrm{185}+\mathrm{65}=\mathrm{250} \\ $$$$\Rightarrow{u}=\mathrm{5}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\Rightarrow{v}=\frac{\mathrm{185}}{\mathrm{5}}−\mathrm{5}^{\mathrm{2}} =\mathrm{12}={xy} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{25}\:\Rightarrow\left({x}+{y}\right)^{\mathrm{2}} =\mathrm{25}+\mathrm{2}×\mathrm{12}=\mathrm{49} \\ $$$$\Rightarrow{x}+{y}=\pm\mathrm{7} \\ $$$$\Rightarrow\left({x},{y}\right)=\left(\mathrm{3},\mathrm{4}\right)\:{or}\:\left(\mathrm{4},\mathrm{3}\right)\:{or}\:\left(−\mathrm{3},−\mathrm{4}\right)\:{or}\:\left(−\mathrm{4},−\mathrm{3}\right) \\ $$
Commented by Acem last updated on 02/Dec/22

$${Neat}\:{Solution}! \\ $$
Answered by Rasheed.Sindhi last updated on 02/Dec/22
![(x^2 +xy+y^2 )(√(x^2 +y^2 )) =185....(i) (x^2 −xy+y^2 )(√(x^2 +y^2 )) =65....(ii) [(√(x^2 +y^2 )) ≠0] (i)×13 & (ii)×37 13(x^2 +xy+y^2 )(√(x^2 +y^2 )) =2405...(iii) 37(x^2 −xy+y^2 )(√(x^2 +y^2 )) =2405...(iv) (iii)&(iv): 13(x^2 +xy+y^2 )=37(x^2 −xy+y^2 ) 12x^2 −25xy+12y^2 =0 ((12x^2 )/(25xy))−1+((12y^2 )/(25xy))=0 ((12)/(25))((x/y)+(y/x))=1 t+(1/t)=((25)/(12)) 12t^2 −25t+12=0 t=((25±(√(625−576)))/(24))=((25±7)/(24))=(4/3),(3/4) (x/y)=(4/3),(3/4) 3x=4y ∨ 4x=3y y= ((3x)/4),((4x)/3) y=((3x)/4): (i)⇒(x^2 +x(((3x)/4))+(((3x)/4))^2 )(√(x^2 +(((3x)/4))^2 )) =185 ((16x^2 +12x^2 +9x^2 )/(16))(√((16x^2 +9x^2 )/(16))) =185 ((37x^2 )/(16))∙((5∣x∣)/4)=185 ∣x∣^3 =64 x=±4⇒y=((3(±4))/4)=±3 y= ((4x)/3): (i)⇒(x^2 +x(((4x)/3))+(((4x)/3))^2 )(√(x^2 +(((4x)/3))^2 )) =185 ((9x^2 +12x^2 +16x^2 )/9)(√((9x^2 +16x^2 )/9)) =185 ((37x^2 )/9)∙((5∣x∣)/3)=185 ∣x∣^3 =27⇒x=±3 ⇒y=((4(±3))/3)=±4 (x,y)={(3,4),(4,3),(−3,−4),(−4,−3)}](https://www.tinkutara.com/question/Q181927.png)
$$\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\mathrm{185}….\left({i}\right) \\ $$$$\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\mathrm{65}….\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\neq\mathrm{0}\right] \\ $$$$ \\ $$$$\left({i}\right)×\mathrm{13}\:\:\&\:\left({ii}\right)×\mathrm{37} \\ $$$$\mathrm{13}\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\mathrm{2405}…\left({iii}\right) \\ $$$$\mathrm{37}\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\mathrm{2405}…\left({iv}\right) \\ $$$$\left({iii}\right)\&\left({iv}\right): \\ $$$$\mathrm{13}\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)=\mathrm{37}\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right) \\ $$$$\mathrm{12}{x}^{\mathrm{2}} −\mathrm{25}{xy}+\mathrm{12}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{12}{x}^{\mathrm{2}} }{\mathrm{25}{xy}}−\mathrm{1}+\frac{\mathrm{12}{y}^{\mathrm{2}} }{\mathrm{25}{xy}}=\mathrm{0} \\ $$$$\frac{\mathrm{12}}{\mathrm{25}}\left(\frac{{x}}{{y}}+\frac{{y}}{{x}}\right)=\mathrm{1} \\ $$$${t}+\frac{\mathrm{1}}{{t}}=\frac{\mathrm{25}}{\mathrm{12}} \\ $$$$\mathrm{12}{t}^{\mathrm{2}} −\mathrm{25}{t}+\mathrm{12}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{25}\pm\sqrt{\mathrm{625}−\mathrm{576}}}{\mathrm{24}}=\frac{\mathrm{25}\pm\mathrm{7}}{\mathrm{24}}=\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{3}{x}=\mathrm{4}{y}\:\vee\:\mathrm{4}{x}=\mathrm{3}{y} \\ $$$${y}=\:\frac{\mathrm{3}{x}}{\mathrm{4}},\frac{\mathrm{4}{x}}{\mathrm{3}} \\ $$$${y}=\frac{\mathrm{3}{x}}{\mathrm{4}}: \\ $$$$\left({i}\right)\Rightarrow\left({x}^{\mathrm{2}} +{x}\left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right)+\left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right)^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +\left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right)^{\mathrm{2}} }\:=\mathrm{185} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{16}}\sqrt{\frac{\mathrm{16}{x}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{16}}}\:=\mathrm{185} \\ $$$$\frac{\mathrm{37}{x}^{\mathrm{2}} }{\mathrm{16}}\centerdot\frac{\mathrm{5}\mid{x}\mid}{\mathrm{4}}=\mathrm{185} \\ $$$$\mid{x}\mid^{\mathrm{3}} =\mathrm{64} \\ $$$${x}=\pm\mathrm{4}\Rightarrow{y}=\frac{\mathrm{3}\left(\pm\mathrm{4}\right)}{\mathrm{4}}=\pm\mathrm{3} \\ $$$${y}=\:\frac{\mathrm{4}{x}}{\mathrm{3}}: \\ $$$$\left({i}\right)\Rightarrow\left({x}^{\mathrm{2}} +{x}\left(\frac{\mathrm{4}{x}}{\mathrm{3}}\right)+\left(\frac{\mathrm{4}{x}}{\mathrm{3}}\right)^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +\left(\frac{\mathrm{4}{x}}{\mathrm{3}}\right)^{\mathrm{2}} }\:=\mathrm{185} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{16}{x}^{\mathrm{2}} }{\mathrm{9}}\sqrt{\frac{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{16}{x}^{\mathrm{2}} }{\mathrm{9}}}\:=\mathrm{185} \\ $$$$\:\:\:\frac{\mathrm{37}{x}^{\mathrm{2}} }{\mathrm{9}}\centerdot\frac{\mathrm{5}\mid{x}\mid}{\mathrm{3}}=\mathrm{185} \\ $$$$\:\:\:\mid{x}\mid^{\mathrm{3}} =\mathrm{27}\Rightarrow{x}=\pm\mathrm{3} \\ $$$$\:\:\Rightarrow{y}=\frac{\mathrm{4}\left(\pm\mathrm{3}\right)}{\mathrm{3}}=\pm\mathrm{4} \\ $$$$\left({x},{y}\right)=\left\{\left(\mathrm{3},\mathrm{4}\right),\left(\mathrm{4},\mathrm{3}\right),\left(−\mathrm{3},−\mathrm{4}\right),\left(−\mathrm{4},−\mathrm{3}\right)\right\} \\ $$
Commented by Acem last updated on 02/Dec/22

$${Mr}.\:{Rasheed}\:{thank}\:{you}\:{for}\:{your}\:{efforts}! \\ $$$$\:{Anyway},\:{if}\:{you}\:{didn}'{t}\:{assume}\:{new}\:{variable},\:{you} \\ $$$$\:{can}\:{solve}\:{it}\:{directly}\:{without}\:{multiply}\:{the} \\ $$$$\:{formulas}\:{by}\:\mathrm{13},\:\mathrm{37} \\ $$$$\:{As}\:{you}\:{see}\:{if}\:{we}\:{sum}\:{i},\:{ii}\:{we}\:{will}\:{save}\:{a}\:{lot}\:{of}\:{work} \\ $$$$ \\ $$$$\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\:\mathrm{125}\:\Rightarrow\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\:\mathrm{25}\:…\:{iii} \\ $$$$\:{iii}\:\wedge\:{ii}:\:\mathrm{25}−{xy}=\:\mathrm{13}\:\Rightarrow\:{xy}=\:\mathrm{12}\:…\:{iv} \\ $$$$\:{Now},\:\left({x}+{y}\right)^{\mathrm{2}} \:=\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\:\mathrm{2}{xy}=\:\mathrm{49} \\ $$$$\:\Rightarrow\:{x}+{y}=\:\pm\mathrm{7}\:…\:{v} \\ $$$$\:{iv}\:\wedge\:{v}: \\ $$$$\:\therefore\:\begin{cases}{{x}+{y}=\:\mathrm{7}}\\{\:{xy}=\:\mathrm{12}}\end{cases}\:\:\:{or}\:\:\begin{cases}{{x}+{y}=\:−\mathrm{7}}\\{\:{xy}=\:\mathrm{12}}\end{cases}\:\: \\ $$$$ \\ $$$$\:\Rightarrow\:{S}=\left\{\left(\mathrm{4},\mathrm{3}\right),\:\left(\mathrm{3},\mathrm{4}\right),\:\left(−\mathrm{4},\:−\mathrm{3}\right),\:\left(−\mathrm{3},−\mathrm{4}\right)\right\} \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 02/Dec/22
$${Agree}\:{sir},\:{that}'{s}\:{more}\:{efficient}\:{way}! \\ $$
