Question Number 181903 by Shrinava last updated on 01/Dec/22

Answered by mr W last updated on 02/Dec/22
![at z: the cross−section is (x^2 /a^2 )+(y^2 /b^2 )=1+(z^2 /c^2 ) which is an ellipse with semi−axes: A=(a/( (√(1+(z^2 /c^2 ))))), B=(b/( (√(1+(z^2 /c^2 ))))). the area of the cross−section is then S(z)=πAB=((πab)/(1+(z^2 /c^2 ))) the volume for z∈[−h,h] is V=2∫_0 ^h S(z)dz =2πab∫_0 ^h (dz/(1+(z^2 /c^2 ))) =2πabc∫_0 ^h ((d((z/c)))/(1+((z/x))^2 )) =2πabc[tan^(−1) (z/c)]_0 ^h =2πabc tan^(−1) (h/c) ✓ with h=2 in the question.](https://www.tinkutara.com/question/Q181929.png)
$${at}\:{z}: \\ $$$${the}\:{cross}−{section}\:{is} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}+\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} } \\ $$$${which}\:{is}\:{an}\:{ellipse}\:{with}\:{semi}−{axes}: \\ $$$${A}=\frac{{a}}{\:\sqrt{\mathrm{1}+\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }}},\:{B}=\frac{{b}}{\:\sqrt{\mathrm{1}+\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }}}. \\ $$$${the}\:{area}\:{of}\:{the}\:{cross}−{section}\:{is}\:{then} \\ $$$${S}\left({z}\right)=\pi{AB}=\frac{\pi{ab}}{\mathrm{1}+\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }} \\ $$$${the}\:{volume}\:{for}\:{z}\in\left[−{h},{h}\right]\:{is} \\ $$$${V}=\mathrm{2}\int_{\mathrm{0}} ^{{h}} {S}\left({z}\right){dz} \\ $$$$\:\:=\mathrm{2}\pi{ab}\int_{\mathrm{0}} ^{{h}} \frac{{dz}}{\mathrm{1}+\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }} \\ $$$$\:\:=\mathrm{2}\pi{abc}\int_{\mathrm{0}} ^{{h}} \frac{{d}\left(\frac{{z}}{{c}}\right)}{\mathrm{1}+\left(\frac{{z}}{{x}}\right)^{\mathrm{2}} } \\ $$$$\:\:=\mathrm{2}\pi{abc}\left[\mathrm{tan}^{−\mathrm{1}} \frac{{z}}{{c}}\right]_{\mathrm{0}} ^{{h}} \\ $$$$\:\:=\mathrm{2}\pi{abc}\:\mathrm{tan}^{−\mathrm{1}} \frac{{h}}{{c}}\:\checkmark \\ $$$${with}\:{h}=\mathrm{2}\:{in}\:{the}\:{question}. \\ $$
Commented by Shrinava last updated on 05/Dec/22
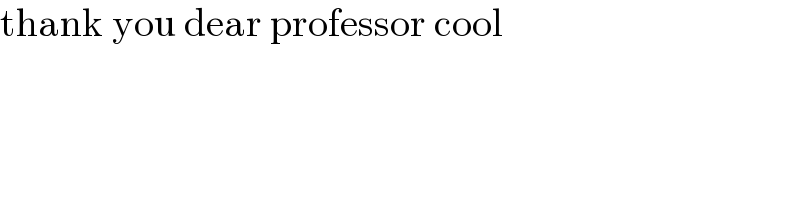
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{cool} \\ $$
