Question-181918

Question Number 181918 by HeferH last updated on 02/Dec/22

Answered by Acem last updated on 02/Dec/22

Commented by Acem last updated on 02/Dec/22

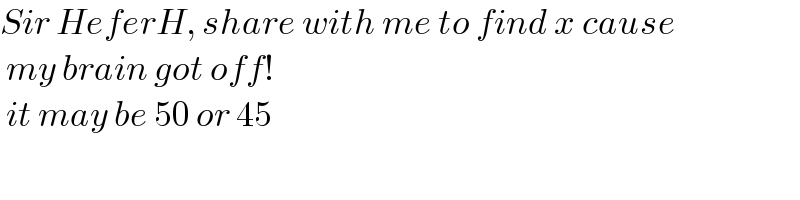
Sir HeferH, share with me to find x cause my brain got off! it may be 50 or 45

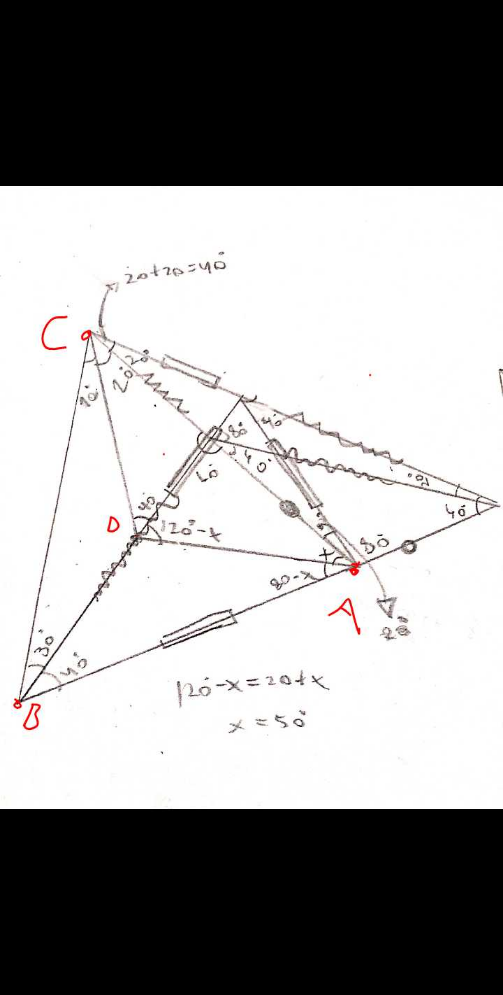
$${Sir}\:{HeferH},\:{share}\:{with}\:{me}\:{to}\:{find}\:{x}\:{cause} \\ $$$$\:{my}\:{brain}\:{got}\:{off}! \\ $$$$\:{it}\:{may}\:{be}\:\mathrm{50}\:{or}\:\mathrm{45} \\ $$

Commented by Acem last updated on 02/Dec/22

The ratio of (x/(80−x)) depends on the height of the isocelles trapezoid, 2 bases are parallels

$${The}\:{ratio}\:{of}\:\frac{{x}}{\mathrm{80}−{x}}\:{depends}\:{on}\:{the}\:{height}\:{of}\:{the} \\ $$$$\:{isocelles}\:{trapezoid},\:\mathrm{2}\:{bases}\:{are}\:{parallels} \\ $$$$ \\ $$

Commented by HeferH last updated on 02/Dec/22

$${Currently},\:{I}\:{also}\:{cannot}\:{find}\:{the}\:{answer}\: \\ $$

Commented by Acem last updated on 02/Dec/22

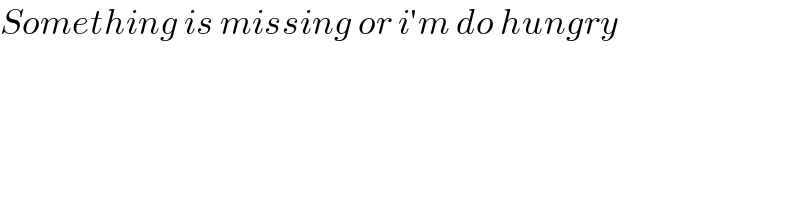
$${Something}\:{is}\:{missing}\:{or}\:{i}'{m}\:{do}\:{hungry} \\ $$

Commented by HeferH last updated on 02/Dec/22

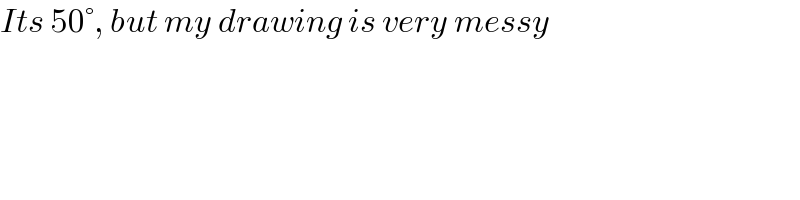
$${Its}\:\mathrm{50}°,\:{but}\:{my}\:{drawing}\:{is}\:{very}\:{messy}\: \\ $$

Answered by HeferH last updated on 02/Dec/22

Commented by Acem last updated on 02/Dec/22

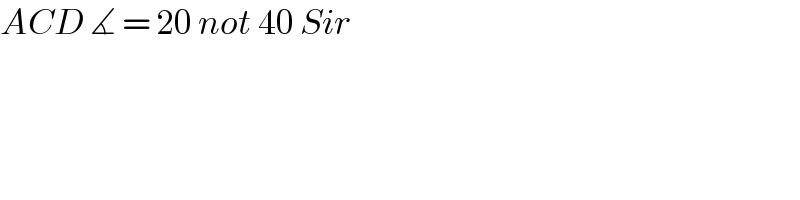
$${ACD}\:\measuredangle\:=\:\mathrm{20}\:{not}\:\mathrm{40}\:{Sir} \\ $$

Commented by HeferH last updated on 02/Dec/22

$${Its}\:{a}\:{external}\:{construction}\: \\ $$

Commented by HeferH last updated on 02/Dec/22

Commented by Acem last updated on 02/Dec/22

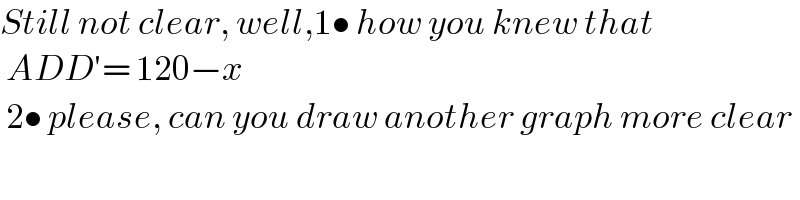
Still not clear, well,1• how you knew that ADD′= 120−x 2• please, can you draw another graph more clear

$${Still}\:{not}\:{clear},\:{well},\mathrm{1}\bullet\:{how}\:{you}\:{knew}\:{that} \\ $$$$\:{ADD}'=\:\mathrm{120}−{x} \\ $$$$\:\mathrm{2}\bullet\:{please},\:{can}\:{you}\:{draw}\:{another}\:{graph}\:{more}\:{clear} \\ $$

Commented by HeferH last updated on 02/Dec/22

1. 80 − x + 40 = 120 − x (exterior angle theorem) 2. Yes, I will work on that, the solution is kinda crazy

$$\mathrm{1}.\:\mathrm{80}\:−\:{x}\:+\:\mathrm{40}\:=\:\mathrm{120}\:−\:{x} \\ $$$$\:\left({exterior}\:{angle}\:{theorem}\right) \\ $$$$\:\mathrm{2}.\:{Yes},\:{I}\:{will}\:{work}\:{on}\:{that},\:{the}\:{solution} \\ $$$$\:{is}\:{kinda}\:{crazy}\: \\ $$

Commented by HeferH last updated on 02/Dec/22

$${btw},\:{those}\:{rectangles},\:{circles}\:{and}\:{curved} \\ $$$$\:{lines}\:{mean}\:{equal}\:{segments} \\ $$

Answered by SEKRET last updated on 02/Dec/22

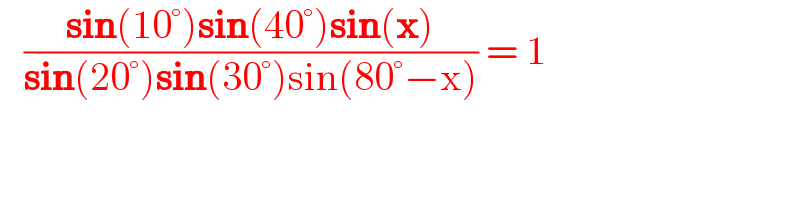
((sin(10°)sin(40°)sin(x))/(sin(20°)sin(30°)sin(80°−x))) = 1

$$\:\:\:\frac{\boldsymbol{\mathrm{sin}}\left(\mathrm{10}°\right)\boldsymbol{\mathrm{sin}}\left(\mathrm{40}°\right)\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{sin}}\left(\mathrm{20}°\right)\boldsymbol{\mathrm{sin}}\left(\mathrm{30}°\right)\mathrm{sin}\left(\mathrm{80}°−\mathrm{x}\right)}\:=\:\mathrm{1} \\ $$

Commented by Frix last updated on 02/Dec/22

$$\Rightarrow\:{x}=\mathrm{50}° \\ $$

Answered by Frix last updated on 03/Dec/22

Let CD=1 and simply use ((sin α)/a)=((sin β)/b)=((sin γ)/c) in each of the triangles ⇒ AB=((sin 40°)/(cos 10°)) BC=2sin 40° CA=((cos 20°)/(cos 40°)) AD=((sin 20°)/(cos 40°)) BD=2sin 10° CD=1 x=50°

$$\mathrm{Let}\:{CD}=\mathrm{1}\:\mathrm{and}\:\mathrm{simply}\:\mathrm{use} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{a}}=\frac{\mathrm{sin}\:\beta}{{b}}=\frac{\mathrm{sin}\:\gamma}{{c}}\:\mathrm{in}\:\mathrm{each}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangles} \\ $$$$\Rightarrow \\ $$$${AB}=\frac{\mathrm{sin}\:\mathrm{40}°}{\mathrm{cos}\:\mathrm{10}°} \\ $$$${BC}=\mathrm{2sin}\:\mathrm{40}° \\ $$$${CA}=\frac{\mathrm{cos}\:\mathrm{20}°}{\mathrm{cos}\:\mathrm{40}°} \\ $$$${AD}=\frac{\mathrm{sin}\:\mathrm{20}°}{\mathrm{cos}\:\mathrm{40}°} \\ $$$${BD}=\mathrm{2sin}\:\mathrm{10}° \\ $$$${CD}=\mathrm{1} \\ $$$${x}=\mathrm{50}° \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply