Question-181987

Question Number 181987 by Acem last updated on 03/Dec/22

Answered by Frix last updated on 03/Dec/22

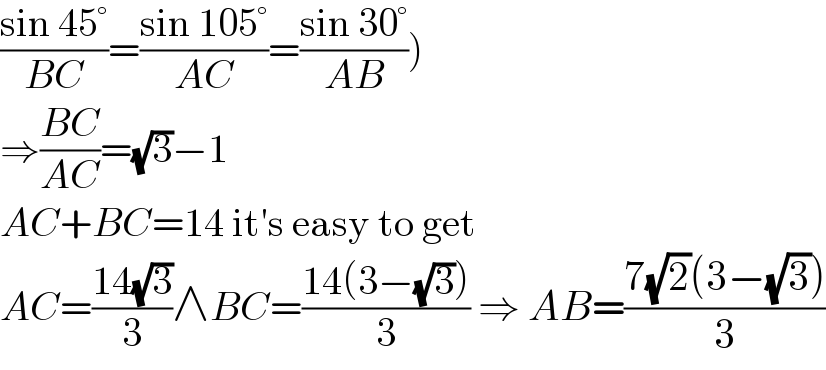
((sin 45°)/(BC))=((sin 105°)/(AC))=((sin 30°)/(AB))) ⇒((BC)/(AC))=(√3)−1 AC+BC=14 it′s easy to get AC=((14(√3))/3)∧BC=((14(3−(√3)))/3) ⇒ AB=((7(√2)(3−(√3)))/3)

$$\left.\frac{\mathrm{sin}\:\mathrm{45}°}{{BC}}=\frac{\mathrm{sin}\:\mathrm{105}°}{{AC}}=\frac{\mathrm{sin}\:\mathrm{30}°}{{AB}}\right) \\ $$$$\Rightarrow\frac{{BC}}{{AC}}=\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$${AC}+{BC}=\mathrm{14}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{get} \\ $$$${AC}=\frac{\mathrm{14}\sqrt{\mathrm{3}}}{\mathrm{3}}\wedge{BC}=\frac{\mathrm{14}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{3}}\:\Rightarrow\:{AB}=\frac{\mathrm{7}\sqrt{\mathrm{2}}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{3}} \\ $$

Commented by Acem last updated on 03/Dec/22

$${Thanks}\:{Sir}! \\ $$

Answered by mr W last updated on 03/Dec/22

Commented by mr W last updated on 03/Dec/22

AD=14 AB=((sin 15)/(sin 120))×14=((7(3(√2)−(√6)))/( 3)) BD=((sin 45)/(sin 120))×14=((14(√6))/3) BC=((BD)/(2 cos 15))=((14(3−(√3)))/3) AC=14−((14(3−(√3)))/3)=((14(√3))/3)

$${AD}=\mathrm{14} \\ $$$${AB}=\frac{\mathrm{sin}\:\mathrm{15}}{\mathrm{sin}\:\mathrm{120}}×\mathrm{14}=\frac{\mathrm{7}\left(\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}\right)}{\:\mathrm{3}} \\ $$$${BD}=\frac{\mathrm{sin}\:\mathrm{45}}{\mathrm{sin}\:\mathrm{120}}×\mathrm{14}=\frac{\mathrm{14}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$${BC}=\frac{{BD}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{15}}=\frac{\mathrm{14}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{3}} \\ $$$${AC}=\mathrm{14}−\frac{\mathrm{14}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{3}}=\frac{\mathrm{14}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$

Commented by Acem last updated on 03/Dec/22

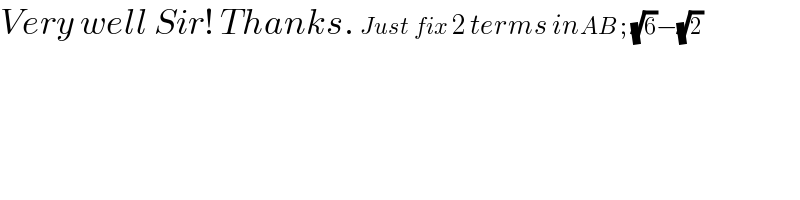
Very well Sir! Thanks. Just fix 2 terms inAB ; (√6)−(√2)

$${Very}\:{well}\:{Sir}!\:{Thanks}.\:{Just}\:{fix}\:\mathrm{2}\:{terms}\:{inAB}\:;\:\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}} \\ $$

Answered by Acem last updated on 03/Dec/22

Four methods to solve Our fiends mr. Frix and mr. W beside to two important formulas 3• ((a+ b)/c)= ((cos (1/2) (α−β))/(sin (1/2) γ)) ⇒c= ∣AB∣= 4.184= ((7(√2))/3) (3−(√3)) 4• ((a−b)/(a+b))= ((tan (1/2) (α−β))/(tan (1/2) (α+β))) ⇒ a−b= −2.165= ((−1)/( (√3) (2+(√3)))) hence we find a=∣BC∣ , b= ∣AC∣ then compt the rest by sine laws ⊛ I prefer extend AC method although the 3rd one is the fasted. Thanks my brothers for sharing!

$${Four}\:{methods}\:{to}\:{solve} \\ $$$$\:{Our}\:{fiends}\:{mr}.\:{Frix}\:{and}\:{mr}.\:{W} \\ $$$$\:{beside}\:{to}\:{two}\:{important}\:{formulas} \\ $$$$\:\mathrm{3}\bullet\:\frac{{a}+\:{b}}{{c}}=\:\frac{\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\alpha−\beta\right)}{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\:\gamma}\:\Rightarrow{c}=\:\mid{AB}\mid=\:\mathrm{4}.\mathrm{184}=\:\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{3}}\:\left(\mathrm{3}−\sqrt{\mathrm{3}}\right) \\ $$$$\mathrm{4}\bullet\:\frac{{a}−{b}}{{a}+{b}}=\:\frac{\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\alpha−\beta\right)}{\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\alpha+\beta\right)}\:\Rightarrow\:{a}−{b}=\:−\mathrm{2}.\mathrm{165}=\:\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \\ $$$$\:{hence}\:{we}\:{find}\:{a}=\mid{BC}\mid\:,\:{b}=\:\mid{AC}\mid \\ $$$$\:{then}\:{compt}\:{the}\:{rest}\:{by}\:{sine}\:{laws} \\ $$$$ \\ $$$$\circledast\:{I}\:{prefer}\:{extend}\:{AC}\:{method}\:{although}\:{the}\:\mathrm{3}{rd}\:{one} \\ $$$$\:{is}\:{the}\:{fasted}. \\ $$$$ \\ $$$$\:{Thanks}\:{my}\:{brothers}\:{for}\:{sharing}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply