Question Number 182001 by mr W last updated on 03/Dec/22
Commented by mr W last updated on 03/Dec/22
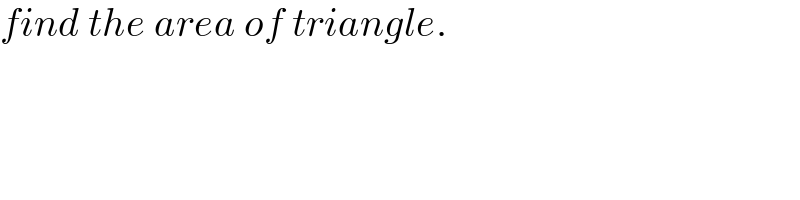
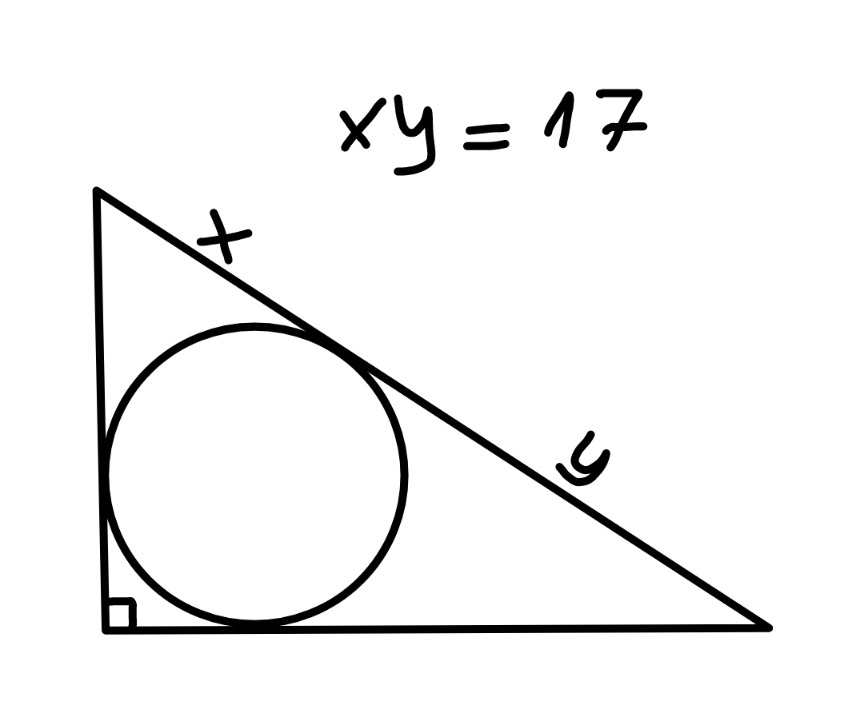
$${find}\:{the}\:{area}\:{of}\:{triangle}. \\ $$
Answered by som(math1967) last updated on 03/Dec/22
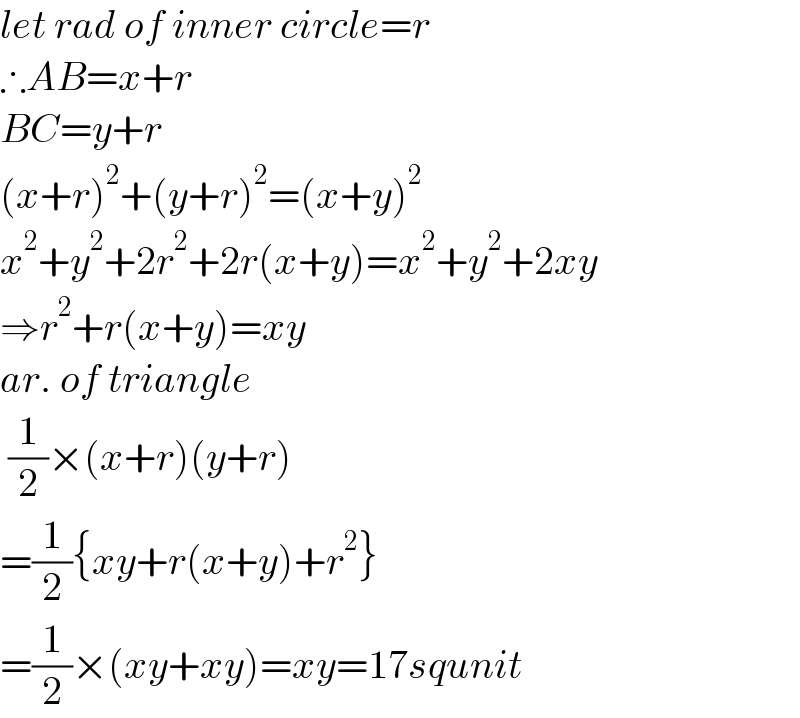
$${let}\:{rad}\:{of}\:{inner}\:{circle}={r} \\ $$$$\therefore{AB}={x}+{r} \\ $$$${BC}={y}+{r} \\ $$$$\left({x}+{r}\right)^{\mathrm{2}} +\left({y}+{r}\right)^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} +\mathrm{2}{r}\left({x}+{y}\right)={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy} \\ $$$$\Rightarrow{r}^{\mathrm{2}} +{r}\left({x}+{y}\right)={xy} \\ $$$${ar}.\:{of}\:{triangle} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}×\left({x}+{r}\right)\left({y}+{r}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{xy}+{r}\left({x}+{y}\right)+{r}^{\mathrm{2}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\left({xy}+{xy}\right)={xy}=\mathrm{17}{squnit} \\ $$
Commented by som(math1967) last updated on 03/Dec/22
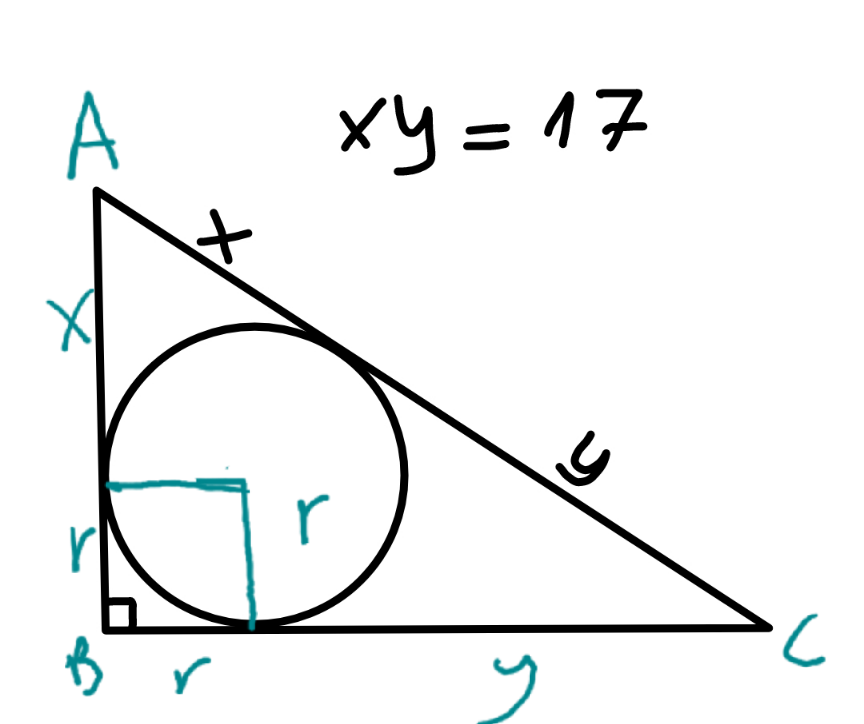
Commented by mr W last updated on 03/Dec/22

$${thanks}! \\ $$
Answered by SEKRET last updated on 03/Dec/22
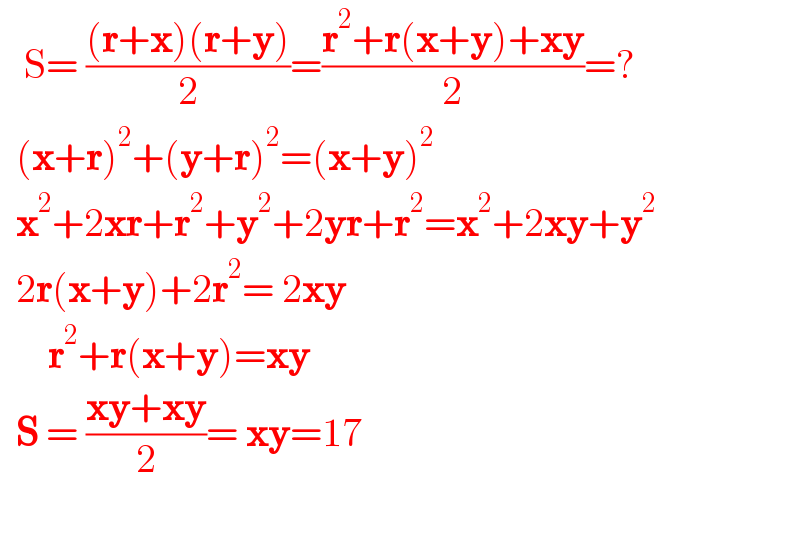
$$\:\:\:\mathrm{S}=\:\frac{\left(\boldsymbol{\mathrm{r}}+\boldsymbol{\mathrm{x}}\right)\left(\boldsymbol{\mathrm{r}}+\boldsymbol{\mathrm{y}}\right)}{\mathrm{2}}=\frac{\boldsymbol{\mathrm{r}}^{\mathrm{2}} +\boldsymbol{\mathrm{r}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)+\boldsymbol{\mathrm{xy}}}{\mathrm{2}}=? \\ $$$$\:\:\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{r}}\right)^{\mathrm{2}} +\left(\boldsymbol{\mathrm{y}}+\boldsymbol{\mathrm{r}}\right)^{\mathrm{2}} =\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)^{\mathrm{2}} \\ $$$$\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{xr}}+\boldsymbol{\mathrm{r}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{yr}}+\boldsymbol{\mathrm{r}}^{\mathrm{2}} =\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{xy}}+\boldsymbol{\mathrm{y}}^{\mathrm{2}} \\ $$$$\:\:\mathrm{2}\boldsymbol{\mathrm{r}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)+\mathrm{2}\boldsymbol{\mathrm{r}}^{\mathrm{2}} =\:\mathrm{2}\boldsymbol{\mathrm{xy}} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{r}}^{\mathrm{2}} +\boldsymbol{\mathrm{r}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)=\boldsymbol{\mathrm{xy}} \\ $$$$\:\:\boldsymbol{\mathrm{S}}\:=\:\frac{\boldsymbol{\mathrm{xy}}+\boldsymbol{\mathrm{xy}}}{\mathrm{2}}=\:\boldsymbol{\mathrm{xy}}=\mathrm{17} \\ $$$$ \\ $$
Commented by mr W last updated on 03/Dec/22

$${thanks}! \\ $$
