Menu Close

Question-182103

Tinku Tara 0 Comments
Pin




Question Number 182103 by mr W last updated on 04/Dec/22
Commented by mr W last updated on 04/Dec/22
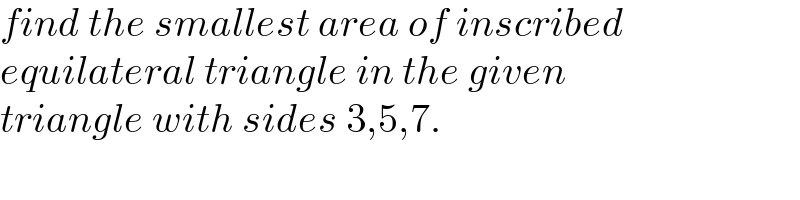
find the smallest area of inscribed equilateral triangle in the given triangle with sides 3,5,7.
$${find}\:{the}\:{smallest}\:{area}\:{of}\:{inscribed}\: \\ $$$${equilateral}\:{triangle}\:{in}\:{the}\:{given}\: \\ $$$${triangle}\:{with}\:{sides}\:\mathrm{3},\mathrm{5},\mathrm{7}. \\ $$
Answered by CrispyXYZ last updated on 04/Dec/22
Theorem The side of the smallest inscribed equilateral triangle of △ABC is ((2S)/( (√K))), where K=(1/2)(a^2 +b^2 +c^2 )+2(√3)S. let n=side of the inscribed triangle S=((15(√3))/4) K=64 n=((15(√3))/(16)) S_2 =((√3)/4)n^2 =((675(√3))/(1024))
$$\boldsymbol{\mathrm{Theorem}}\:\mathrm{The}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{inscribed} \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{of}\:\bigtriangleup{ABC}\:\mathrm{is}\:\frac{\mathrm{2}{S}}{\:\sqrt{{K}}}, \\ $$$$\mathrm{where}\:{K}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2}\sqrt{\mathrm{3}}{S}. \\ $$$$ \\ $$$$\mathrm{let}\:{n}=\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{inscribed}\:\mathrm{triangle} \\ $$$${S}=\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$${K}=\mathrm{64} \\ $$$${n}=\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{16}} \\ $$$${S}_{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{n}^{\mathrm{2}} =\frac{\mathrm{675}\sqrt{\mathrm{3}}}{\mathrm{1024}} \\ $$
Commented by CrispyXYZ last updated on 04/Dec/22
The position of the inscribed triangle. Order: black→cyan→green→red
$$\mathrm{The}\:\mathrm{position}\:\mathrm{of}\:\mathrm{the}\:\mathrm{inscribed}\:\mathrm{triangle}. \\ $$$$\mathrm{Order}:\:\mathrm{black}\rightarrow\mathrm{cyan}\rightarrow\mathrm{green}\rightarrow\mathrm{red} \\ $$
Commented by CrispyXYZ last updated on 04/Dec/22
Commented by mr W last updated on 04/Dec/22
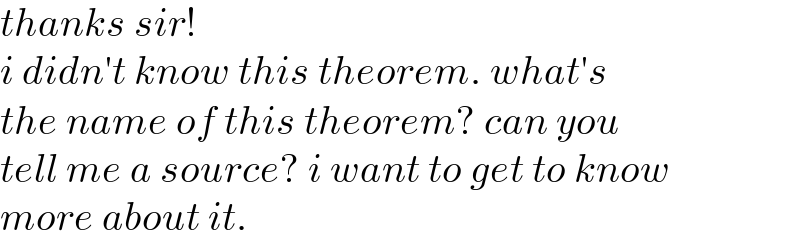
thanks sir! i didn′t know this theorem. what′s the name of this theorem? can you tell me a source? i want to get to know more about it.
$${thanks}\:{sir}! \\ $$$${i}\:{didn}'{t}\:{know}\:{this}\:{theorem}.\:{what}'{s} \\ $$$${the}\:{name}\:{of}\:{this}\:{theorem}?\:{can}\:{you} \\ $$$${tell}\:{me}\:{a}\:{source}?\:{i}\:{want}\:{to}\:{get}\:{to}\:{know} \\ $$$${more}\:{about}\:{it}. \\ $$
Commented by CrispyXYZ last updated on 05/Dec/22
It is from a journal in China. DOI: 10.3969/j.issn.1002-4123.2003.03.025 Below is the proof in English. Let ∠C is the largest angle in △ABC, △DEF is any inscribed regular triangle (as shown below), ∠FDB=α, FD=x. Then, ∠EDC=120°−α, ∠DEC=60°+α−∠C, ∠AEF=60°−α+∠C BF=((x sinα)/(sinB)), FA=((x sin(60°−α+C))/(sinA)) (The Law of Sines) Therefore, c = BA = BF + FA = ((x(sinA sinα + sinB sin(60°+C−α)))/(sinA sinB)) x=((c sinA sinB)/(sinA sinα + sinB sin(60°+C−α))) Let L=sinA sinα + sinB sin(60°+C−α) =sinAsinα+sinB(sin(60°+C)cosα−cos(60°+C)sinα) =(sinA−sinBcos(60°+C))sinα+sinBsin(60°+C)cosα Let tanϕ=((sinB sin(60°+C))/(sinA−sinBcos(60°+C))), 0≤ϕ≤π (use the auxiliary angle method, aka R method) L=(√((sinA−sinBcos(60°+C))^2 +(sinBsin(60°+C))^2 ))sin(α+ϕ) =(√(sin^2 A+sin^2 B−2sinAsinBcos(60°+C)))sin(α+ϕ) (use The Law of Sines) =(1/(2R))(√(a^2 +b^2 −2abcos(C+60°)))sin(α+ϕ) =(1/(2R))(√((1/2)(a^2 +b^2 +c^2 )+2(√3)S))∙sin(α+ϕ) Let K=(1/2)(a^2 +b^2 +c^2 )+2(√3)S Then, L≤((√K)/(2R)) if and only if sin(α+ϕ)=1, (that is, α+ϕ=(π/2),) L=((√K)/(2R)) is true. Therefore, x=((c sinA sinB)/L)≥((2Rc sinA sinB)/( (√K)))=((2S)/( (√K))) x_(min) =((2S)/( (√K)))
$$\mathrm{It}\:\mathrm{is}\:\mathrm{from}\:\mathrm{a}\:\mathrm{journal}\:\mathrm{in}\:\mathrm{China}. \\ $$$$\mathrm{DOI}: \\ $$10.3969/j.issn.1002-4123.2003.03.025
$$\mathrm{Below}\:\mathrm{is}\:\mathrm{the}\:\mathrm{proof}\:\mathrm{in}\:\mathrm{English}. \\ $$$$\mathrm{Let}\:\angle{C}\:\mathrm{is}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{angle}\:\mathrm{in}\:\bigtriangleup{ABC}, \\ $$$$\bigtriangleup{DEF}\:\mathrm{is}\:\mathrm{any}\:\mathrm{inscribed}\:\mathrm{regular}\:\mathrm{triangle}\:\left(\mathrm{as}\:\mathrm{shown}\:\mathrm{below}\right), \\ $$$$\angle{FDB}=\alpha,\:{FD}={x}. \\ $$$$\mathrm{Then},\:\angle{EDC}=\mathrm{120}°−\alpha,\:\angle{DEC}=\mathrm{60}°+\alpha−\angle{C}, \\ $$$$\angle{AEF}=\mathrm{60}°−\alpha+\angle{C} \\ $$$${BF}=\frac{{x}\:\mathrm{sin}\alpha}{\mathrm{sin}{B}},\:{FA}=\frac{{x}\:\mathrm{sin}\left(\mathrm{60}°−\alpha+{C}\right)}{\mathrm{sin}{A}}\:\left(\mathrm{The}\:\mathrm{Law}\:\mathrm{of}\:\mathrm{Sines}\right) \\ $$$$\mathrm{Therefore}, \\ $$$${c}\:=\:{BA}\:=\:{BF}\:+\:{FA}\:= \\ $$$$\frac{{x}\left(\mathrm{sin}{A}\:\mathrm{sin}\alpha\:+\:\mathrm{sin}{B}\:\mathrm{sin}\left(\mathrm{60}°+{C}−\alpha\right)\right)}{\mathrm{sin}{A}\:\mathrm{sin}{B}} \\ $$$${x}=\frac{{c}\:\mathrm{sin}{A}\:\mathrm{sin}{B}}{\mathrm{sin}{A}\:\mathrm{sin}\alpha\:+\:\mathrm{sin}{B}\:\mathrm{sin}\left(\mathrm{60}°+{C}−\alpha\right)} \\ $$$$\mathrm{Let}\:{L}=\mathrm{sin}{A}\:\mathrm{sin}\alpha\:+\:\mathrm{sin}{B}\:\mathrm{sin}\left(\mathrm{60}°+{C}−\alpha\right) \\ $$$$=\mathrm{sin}{A}\mathrm{sin}\alpha+\mathrm{sin}{B}\left(\mathrm{sin}\left(\mathrm{60}°+{C}\right)\mathrm{cos}\alpha−\mathrm{cos}\left(\mathrm{60}°+{C}\right)\mathrm{sin}\alpha\right) \\ $$$$=\left(\mathrm{sin}{A}−\mathrm{sin}{B}\mathrm{cos}\left(\mathrm{60}°+{C}\right)\right)\mathrm{sin}\alpha+\mathrm{sin}{B}\mathrm{sin}\left(\mathrm{60}°+{C}\right)\mathrm{cos}\alpha \\ $$$$\mathrm{Let}\:\mathrm{tan}\varphi=\frac{\mathrm{sin}{B}\:\mathrm{sin}\left(\mathrm{60}°+{C}\right)}{\mathrm{sin}{A}−\mathrm{sin}{B}\mathrm{cos}\left(\mathrm{60}°+{C}\right)},\:\mathrm{0}\leqslant\varphi\leqslant\pi \\ $$$$\left(\mathrm{use}\:\mathrm{the}\:\mathrm{auxiliary}\:\mathrm{angle}\:\mathrm{method},\:\mathrm{aka}\:\mathrm{R}\:\mathrm{method}\right) \\ $$$${L}=\sqrt{\left(\mathrm{sin}{A}−\mathrm{sin}{B}\mathrm{cos}\left(\mathrm{60}°+{C}\right)\right)^{\mathrm{2}} +\left(\mathrm{sin}{B}\mathrm{sin}\left(\mathrm{60}°+{C}\right)\right)^{\mathrm{2}} }\mathrm{sin}\left(\alpha+\varphi\right) \\ $$$$=\sqrt{\mathrm{sin}^{\mathrm{2}} {A}+\mathrm{sin}^{\mathrm{2}} {B}−\mathrm{2sin}{A}\mathrm{sin}{B}\mathrm{cos}\left(\mathrm{60}°+{C}\right)}\mathrm{sin}\left(\alpha+\varphi\right) \\ $$$$\left(\mathrm{use}\:\mathrm{The}\:\mathrm{Law}\:\mathrm{of}\:\mathrm{Sines}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{R}}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\left({C}+\mathrm{60}°\right)}\mathrm{sin}\left(\alpha+\varphi\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{R}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2}\sqrt{\mathrm{3}}{S}}\centerdot\mathrm{sin}\left(\alpha+\varphi\right) \\ $$$$\mathrm{Let}\:{K}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2}\sqrt{\mathrm{3}}{S} \\ $$$$\mathrm{Then},\:{L}\leqslant\frac{\sqrt{{K}}}{\mathrm{2}{R}} \\ $$$$\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{sin}\left(\alpha+\varphi\right)=\mathrm{1},\:\left(\mathrm{that}\:\mathrm{is},\:\alpha+\varphi=\frac{\pi}{\mathrm{2}},\right)\:{L}=\frac{\sqrt{{K}}}{\mathrm{2}{R}}\:\mathrm{is}\:\mathrm{true}. \\ $$$$\mathrm{Therefore},\:{x}=\frac{{c}\:\mathrm{sin}{A}\:\mathrm{sin}{B}}{{L}}\geqslant\frac{\mathrm{2}{Rc}\:\mathrm{sin}{A}\:\mathrm{sin}{B}}{\:\sqrt{{K}}}=\frac{\mathrm{2}{S}}{\:\sqrt{{K}}} \\ $$$${x}_{\mathrm{min}} =\frac{\mathrm{2}{S}}{\:\sqrt{{K}}} \\ $$
Commented by CrispyXYZ last updated on 05/Dec/22
Commented by mr W last updated on 05/Dec/22
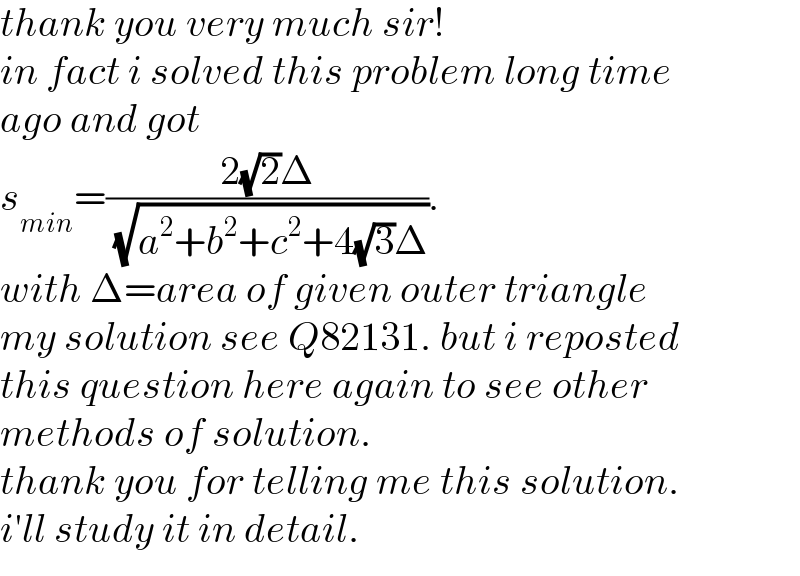
thank you very much sir! in fact i solved this problem long time ago and got s_(min) =((2(√2)Δ)/( (√(a^2 +b^2 +c^2 +4(√3)Δ)))). with Δ=area of given outer triangle my solution see Q82131. but i reposted this question here again to see other methods of solution. thank you for telling me this solution. i′ll study it in detail.
$${thank}\:{you}\:{very}\:{much}\:{sir}! \\ $$$${in}\:{fact}\:{i}\:{solved}\:{this}\:{problem}\:{long}\:{time} \\ $$$${ago}\:{and}\:{got} \\ $$$${s}_{{min}} =\frac{\mathrm{2}\sqrt{\mathrm{2}}\Delta}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\Delta}}. \\ $$$${with}\:\Delta={area}\:{of}\:{given}\:{outer}\:{triangle} \\ $$$${my}\:{solution}\:{see}\:{Q}\mathrm{82131}.\:{but}\:{i}\:{reposted} \\ $$$${this}\:{question}\:{here}\:{again}\:{to}\:{see}\:{other} \\ $$$${methods}\:{of}\:{solution}. \\ $$$${thank}\:{you}\:{for}\:{telling}\:{me}\:{this}\:{solution}. \\ $$$${i}'{ll}\:{study}\:{it}\:{in}\:{detail}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *