Question Number 182176 by peter frank last updated on 05/Dec/22

Answered by MikeH last updated on 05/Dec/22
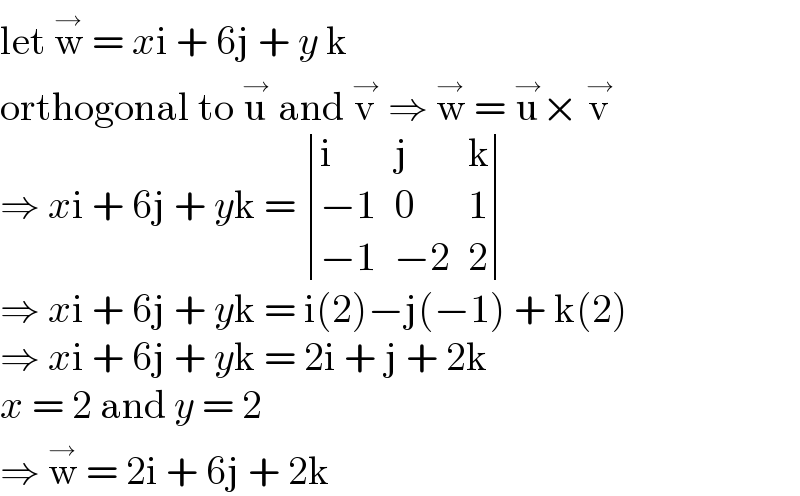
$$\mathrm{let}\:\overset{\rightarrow} {\mathrm{w}}\:=\:{x}\mathrm{i}\:+\:\mathrm{6j}\:+\:{y}\:\mathrm{k} \\ $$$$\mathrm{orthogonal}\:\mathrm{to}\:\overset{\rightarrow} {\mathrm{u}}\:\mathrm{and}\:\overset{\rightarrow} {\mathrm{v}}\:\Rightarrow\:\overset{\rightarrow} {\mathrm{w}}\:=\:\overset{\rightarrow} {\mathrm{u}}×\:\overset{\rightarrow} {\mathrm{v}} \\ $$$$\Rightarrow\:{x}\mathrm{i}\:+\:\mathrm{6j}\:+\:{y}\mathrm{k}\:=\:\begin{vmatrix}{\mathrm{i}}&{\mathrm{j}}&{\mathrm{k}}\\{−\mathrm{1}}&{\mathrm{0}}&{\mathrm{1}}\\{−\mathrm{1}}&{−\mathrm{2}}&{\mathrm{2}}\end{vmatrix} \\ $$$$\Rightarrow\:{x}\mathrm{i}\:+\:\mathrm{6j}\:+\:{y}\mathrm{k}\:=\:\mathrm{i}\left(\mathrm{2}\right)−\mathrm{j}\left(−\mathrm{1}\right)\:+\:\mathrm{k}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\:{x}\mathrm{i}\:+\:\mathrm{6j}\:+\:{y}\mathrm{k}\:=\:\mathrm{2i}\:+\:\mathrm{j}\:+\:\mathrm{2k} \\ $$$${x}\:=\:\mathrm{2}\:\mathrm{and}\:{y}\:=\:\mathrm{2} \\ $$$$\Rightarrow\:\overset{\rightarrow} {\mathrm{w}}\:=\:\mathrm{2i}\:+\:\mathrm{6j}\:+\:\mathrm{2k}\: \\ $$
