Question Number 182311 by mnjuly1970 last updated on 07/Dec/22

Commented by Frix last updated on 07/Dec/22
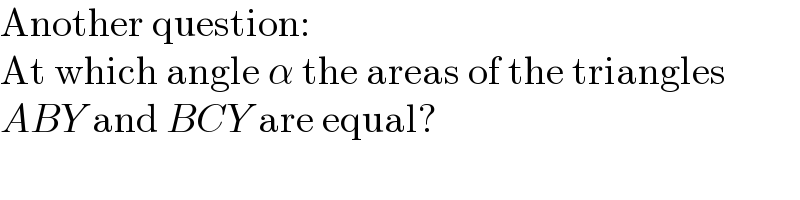
$$\mathrm{Another}\:\mathrm{question}: \\ $$$$\mathrm{At}\:\mathrm{which}\:\mathrm{angle}\:\alpha\:\mathrm{the}\:\mathrm{areas}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangles} \\ $$$${ABY}\:\mathrm{and}\:{BCY}\:\mathrm{are}\:\mathrm{equal}? \\ $$
Commented by Frix last updated on 07/Dec/22
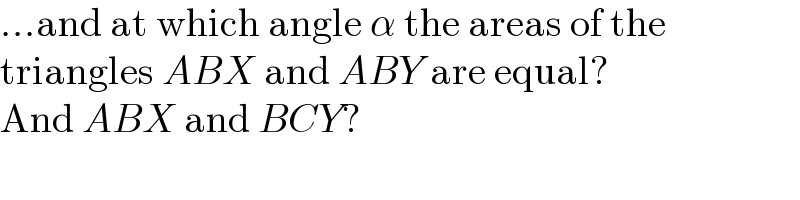
$$…\mathrm{and}\:\mathrm{at}\:\mathrm{which}\:\mathrm{angle}\:\alpha\:\mathrm{the}\:\mathrm{areas}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{triangles}\:{ABX}\:\mathrm{and}\:{ABY}\:\mathrm{are}\:\mathrm{equal}? \\ $$$$\mathrm{And}\:{ABX}\:\mathrm{and}\:{BCY}? \\ $$
Commented by MJS_new last updated on 09/Dec/22
![AB=a AC=b a≤b BC=(√(a^2 +b^2 )) AX=h BX=p CX=q ⇒ Δ_1 =area (aph) =((a^3 b)/(2(a^2 +b^2 ))) Δ_2 =area (bqh) =((ab^3 )/(2(a^2 +b^2 ))) Δ_3 =area (ABY) =(a^4 /(a^2 +b^2 )) Δ_4 =area (BCY) =(((b^3 +a^2 b−2a^3 )a)/(2(a^2 +b^2 ))) we can set b=1 ⇒ 0<a≤b Δ_1 =Δ_2 ⇒ a=1 Δ_1 =Δ_3 ⇒ a=1/2 Δ_1 =Δ_4 ⇒ a=1/(2)^(1/3) Δ_2 =Δ_3 ⇒ a=1/(2)^(1/3) Δ_2 =Δ_4 ⇒ a=1/2 Δ_3 =Δ_4 ⇒ a≈.725270085072 [a=(1/(12))(1+((217−12(√(327))))^(1/3) +((217+12(√(327))))^(1/3) )] calculate the angles, I′m too lazy.](https://www.tinkutara.com/question/Q182468.png)
$${AB}={a}\:\:\:\:\:{AC}={b}\:\:\:\:\:{a}\leqslant{b}\:\:\:\:\:{BC}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${AX}={h}\:\:\:\:\:{BX}={p}\:\:\:\:\:{CX}={q} \\ $$$$\Rightarrow \\ $$$$\Delta_{\mathrm{1}} =\mathrm{area}\:\left({aph}\right)\:=\frac{{a}^{\mathrm{3}} {b}}{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$$\Delta_{\mathrm{2}} =\mathrm{area}\:\left({bqh}\right)\:=\frac{{ab}^{\mathrm{3}} }{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$$\Delta_{\mathrm{3}} =\mathrm{area}\:\left({ABY}\right)\:=\frac{{a}^{\mathrm{4}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Delta_{\mathrm{4}} =\mathrm{area}\:\left({BCY}\right)\:=\frac{\left({b}^{\mathrm{3}} +{a}^{\mathrm{2}} {b}−\mathrm{2}{a}^{\mathrm{3}} \right){a}}{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{set}\:{b}=\mathrm{1}\:\Rightarrow\:\mathrm{0}<{a}\leqslant{b} \\ $$$$\Delta_{\mathrm{1}} =\Delta_{\mathrm{2}} \:\Rightarrow\:{a}=\mathrm{1} \\ $$$$\Delta_{\mathrm{1}} =\Delta_{\mathrm{3}} \:\Rightarrow\:{a}=\mathrm{1}/\mathrm{2} \\ $$$$\Delta_{\mathrm{1}} =\Delta_{\mathrm{4}} \:\Rightarrow\:{a}=\mathrm{1}/\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$$\Delta_{\mathrm{2}} =\Delta_{\mathrm{3}} \:\Rightarrow\:{a}=\mathrm{1}/\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$$\Delta_{\mathrm{2}} =\Delta_{\mathrm{4}} \:\Rightarrow\:{a}=\mathrm{1}/\mathrm{2} \\ $$$$\Delta_{\mathrm{3}} =\Delta_{\mathrm{4}} \:\Rightarrow\:{a}\approx.\mathrm{725270085072}\:\left[{a}=\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{217}−\mathrm{12}\sqrt{\mathrm{327}}}+\sqrt[{\mathrm{3}}]{\mathrm{217}+\mathrm{12}\sqrt{\mathrm{327}}}\right)\right] \\ $$$$\mathrm{calculate}\:\mathrm{the}\:\mathrm{angles},\:\mathrm{I}'\mathrm{m}\:\mathrm{too}\:\mathrm{lazy}. \\ $$
Commented by Frix last updated on 09/Dec/22

$$\mathrm{Thank}\:\mathrm{you}… \\ $$
Commented by Acem last updated on 10/Dec/22

$${Why}\:{losing}\:{calories}\:{by}\:{writing}\:{calculate}\:{the}…{etc} \\ $$$$\:{Next}\:{time}\:{just}\:{write}\:“…''\:{and}\:{the}\:{calculators} \\ $$$$\:{will}\:{complete}\:{the}\:{job}. \\ $$$${Thanks}\:{Sir}! \\ $$
Answered by Acem last updated on 08/Dec/22
![(2/h_(AX) ) − (2/λ_(BY) )= (1/b_(AC) ) ⇔ (2/(c cos α)) − ((2 cos α)/c) = ((tan α)/c) ⇔ 2 sin^2 α= sin α , α= 30° @Mr Frix Total △ABC= (1/2) bc , △ABY = (1/2) x_(AY) c For △ABY= △BCY = (1/2) △ABC at x= (b/2) that mean BY is median ; β_(∡ACB) =30, α ∈ [0, 60] but how to determin α if we have not any side? if you used (1/2) λ_(BY) c sin α, well the area will be= (1/2) c^2 tan α , so how to determine α](https://www.tinkutara.com/question/Q182349.png)
$$\:\frac{\mathrm{2}}{{h}_{{AX}} }\:−\:\frac{\mathrm{2}}{\lambda_{{BY}} }=\:\frac{\mathrm{1}}{{b}_{{AC}} }\:\Leftrightarrow\:\frac{\mathrm{2}}{{c}\:\mathrm{cos}\:\alpha}\:−\:\frac{\mathrm{2}\:\mathrm{cos}\:\alpha}{{c}}\:=\:\frac{\mathrm{tan}\:\alpha}{{c}}\:\Leftrightarrow \\ $$$$\:\:\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\alpha=\:\mathrm{sin}\:\alpha\:,\:\alpha=\:\mathrm{30}° \\ $$$$ \\ $$$$@{Mr}\:{Frix} \\ $$$$\:{Total}\:\bigtriangleup{ABC}=\:\frac{\mathrm{1}}{\mathrm{2}}\:{bc}\:,\:\bigtriangleup{ABY}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:{x}_{{AY}} \:{c} \\ $$$$\:{For}\:\bigtriangleup{ABY}=\:\bigtriangleup{BCY}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\bigtriangleup{ABC}\:\:{at}\:{x}=\:\frac{{b}}{\mathrm{2}} \\ $$$$\:{that}\:{mean}\:{BY}\:{is}\:{median}\:;\:\beta_{\measuredangle{ACB}} =\mathrm{30},\:\alpha\:\in\:\left[\mathrm{0},\:\mathrm{60}\right] \\ $$$$\:{but}\:{how}\:{to}\:{determin}\:\alpha\:{if}\:{we}\:{have}\:{not}\:{any}\:{side}? \\ $$$$\:{if}\:{you}\:{used}\:\frac{\mathrm{1}}{\mathrm{2}}\:\lambda_{{BY}} \:\:{c}\:\mathrm{sin}\:\alpha,\:{well} \\ $$$$\:{the}\:{area}\:{will}\:{be}=\:\frac{\mathrm{1}}{\mathrm{2}}\:{c}^{\mathrm{2}} \:\mathrm{tan}\:\alpha\:, \\ $$$$\:{so}\:{how}\:{to}\:{determine}\:\alpha \\ $$$$\: \\ $$
Commented by mnjuly1970 last updated on 08/Dec/22

$${thx}\:{sir}\:{Acm} \\ $$
Commented by Acem last updated on 08/Dec/22

$${You}'{re}\:{very}\:{much}\:{welcone},\:{and}\:{thank}\:{you}\:{a}\:{lot} \\ $$$$\:{for}\:{your}\:{featured}\:{qusetions}! \\ $$
Answered by mr W last updated on 07/Dec/22
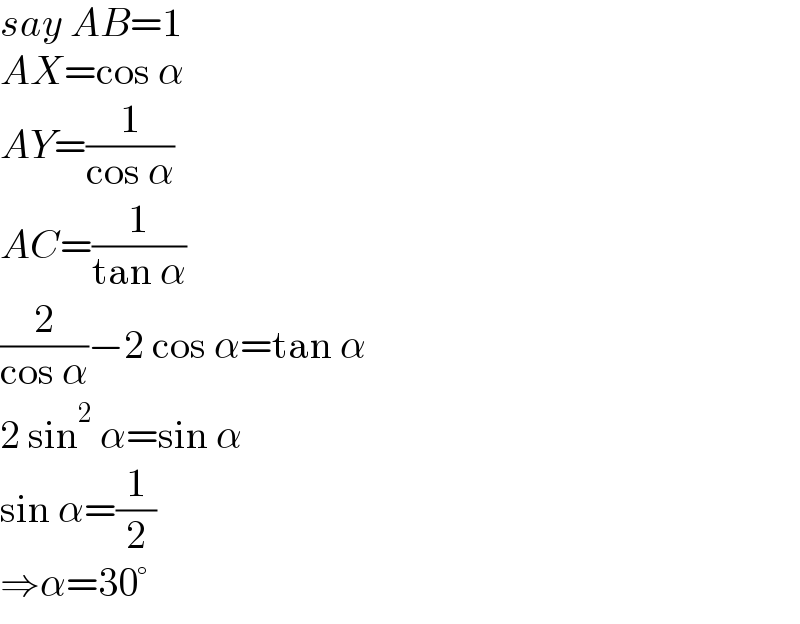
$${say}\:{AB}=\mathrm{1} \\ $$$${AX}=\mathrm{cos}\:\alpha \\ $$$${AY}=\frac{\mathrm{1}}{\mathrm{cos}\:\alpha} \\ $$$${AC}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$$\frac{\mathrm{2}}{\mathrm{cos}\:\alpha}−\mathrm{2}\:\mathrm{cos}\:\alpha=\mathrm{tan}\:\alpha \\ $$$$\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\alpha=\mathrm{sin}\:\alpha \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\alpha=\mathrm{30}° \\ $$
Commented by mnjuly1970 last updated on 07/Dec/22
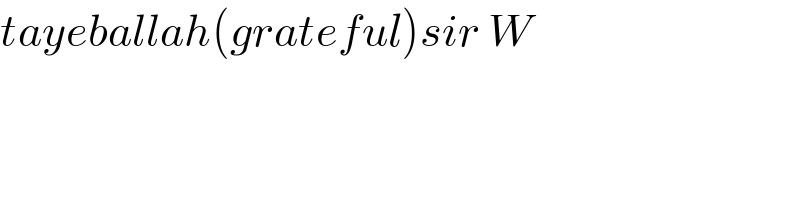
$${tayeballah}\left({grateful}\right){sir}\:{W} \\ $$
