Question Number 182423 by Noorzai last updated on 09/Dec/22

Answered by JDamian last updated on 09/Dec/22
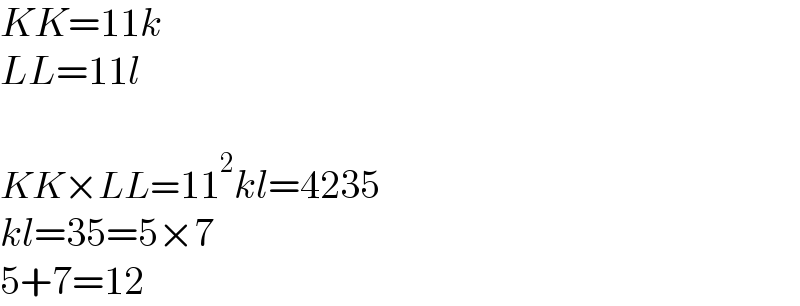
$${KK}=\mathrm{11}{k} \\ $$$${LL}=\mathrm{11}{l} \\ $$$$ \\ $$$${KK}×{LL}=\mathrm{11}^{\mathrm{2}} {kl}=\mathrm{4235} \\ $$$${kl}=\mathrm{35}=\mathrm{5}×\mathrm{7} \\ $$$$\mathrm{5}+\mathrm{7}=\mathrm{12} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Dec/22
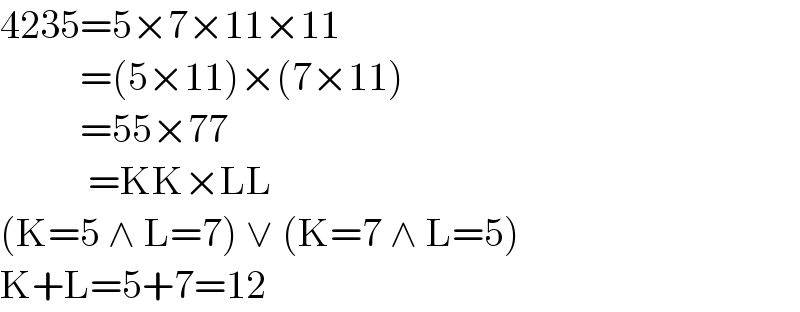
$$\mathrm{4235}=\mathrm{5}×\mathrm{7}×\mathrm{11}×\mathrm{11} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{5}×\mathrm{11}\right)×\left(\mathrm{7}×\mathrm{11}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{55}×\mathrm{77} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{KK}×\mathrm{LL} \\ $$$$\left(\mathrm{K}=\mathrm{5}\:\wedge\:\mathrm{L}=\mathrm{7}\right)\:\vee\:\left(\mathrm{K}=\mathrm{7}\:\wedge\:\mathrm{L}=\mathrm{5}\right) \\ $$$$\mathrm{K}+\mathrm{L}=\mathrm{5}+\mathrm{7}=\mathrm{12} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Dec/22
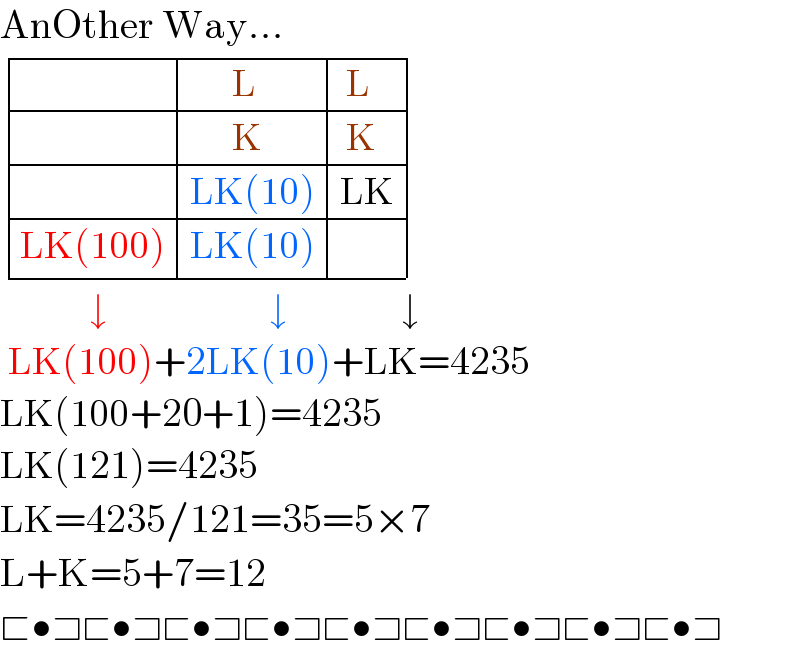
$$\mathrm{AnOther}\:\mathrm{Way}… \\ $$$$\begin{array}{|c|c|c|c|}{}&\hline{\:\:\:\:\:\:\:\mathrm{L}}&\hline{\:\mathrm{L}}\\{}&\hline{\:\:\:\:\:\:\:\mathrm{K}}&\hline{\:\mathrm{K}}\\{}&\hline{\mathrm{LK}\left(\mathrm{10}\right)}&\hline{\mathrm{LK}}\\{\mathrm{LK}\left(\mathrm{100}\right)}&\hline{\mathrm{LK}\left(\mathrm{10}\right)}&\hline{}\\\hline\end{array}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\downarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\downarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\downarrow \\ $$$$\:\mathrm{LK}\left(\mathrm{100}\right)+\mathrm{2LK}\left(\mathrm{10}\right)+\mathrm{LK}=\mathrm{4235} \\ $$$$\mathrm{LK}\left(\mathrm{100}+\mathrm{20}+\mathrm{1}\right)=\mathrm{4235} \\ $$$$\mathrm{LK}\left(\mathrm{121}\right)=\mathrm{4235} \\ $$$$\mathrm{LK}=\mathrm{4235}/\mathrm{121}=\mathrm{35}=\mathrm{5}×\mathrm{7} \\ $$$$\mathrm{L}+\mathrm{K}=\mathrm{5}+\mathrm{7}=\mathrm{12} \\ $$$$\sqsubset\bullet\sqsupset\sqsubset\bullet\sqsupset\sqsubset\bullet\sqsupset\sqsubset\bullet\sqsupset\sqsubset\bullet\sqsupset\sqsubset\bullet\sqsupset\sqsubset\bullet\sqsupset\sqsubset\bullet\sqsupset\sqsubset\bullet\sqsupset \\ $$
Answered by manxsol last updated on 09/Dec/22

