Question-182435

Question Number 182435 by akolade last updated on 09/Dec/22

Answered by Rasheed.Sindhi last updated on 09/Dec/22

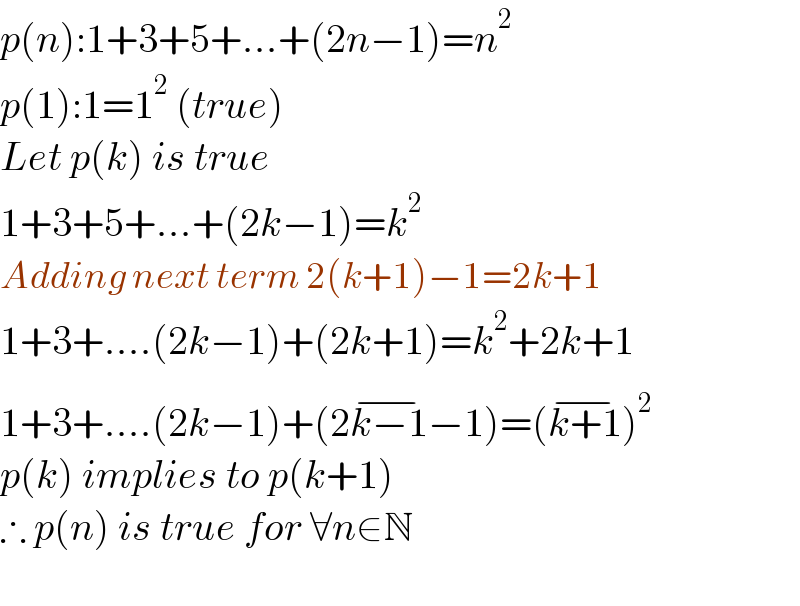
p(n):1+3+5+...+(2n−1)=n^2 p(1):1=1^2 (true) Let p(k) is true 1+3+5+...+(2k−1)=k^2 Adding next term 2(k+1)−1=2k+1 1+3+....(2k−1)+(2k+1)=k^2 +2k+1 1+3+....(2k−1)+(2k−1^(−) −1)=(k+1^(−) )^2 p(k) implies to p(k+1) ∴ p(n) is true for ∀n∈N

$${p}\left({n}\right):\mathrm{1}+\mathrm{3}+\mathrm{5}+…+\left(\mathrm{2}{n}−\mathrm{1}\right)={n}^{\mathrm{2}} \\ $$$${p}\left(\mathrm{1}\right):\mathrm{1}=\mathrm{1}^{\mathrm{2}} \:\left({true}\right) \\ $$$${Let}\:{p}\left({k}\right)\:{is}\:{true} \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{5}+…+\left(\mathrm{2}{k}−\mathrm{1}\right)={k}^{\mathrm{2}} \\ $$$${Adding}\:{next}\:{term}\:\mathrm{2}\left({k}+\mathrm{1}\right)−\mathrm{1}=\mathrm{2}{k}+\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{3}+….\left(\mathrm{2}{k}−\mathrm{1}\right)+\left(\mathrm{2}{k}+\mathrm{1}\right)={k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{3}+….\left(\mathrm{2}{k}−\mathrm{1}\right)+\left(\mathrm{2}\overline {{k}−\mathrm{1}}−\mathrm{1}\right)=\left(\overline {{k}+\mathrm{1}}\right)^{\mathrm{2}} \\ $$$${p}\left({k}\right)\:{implies}\:{to}\:{p}\left({k}+\mathrm{1}\right) \\ $$$$\therefore\:{p}\left({n}\right)\:{is}\:{true}\:{for}\:\forall{n}\in\mathbb{N} \\ $$$$ \\ $$

Facebook Tweet Pin

Question-182435

Leave a Reply Cancel reply