Question Number 182494 by universe last updated on 10/Dec/22

Commented by cortano1 last updated on 11/Dec/22

$$\left(\mathrm{c}\right)\:\pi \\ $$
Commented by mr W last updated on 11/Dec/22
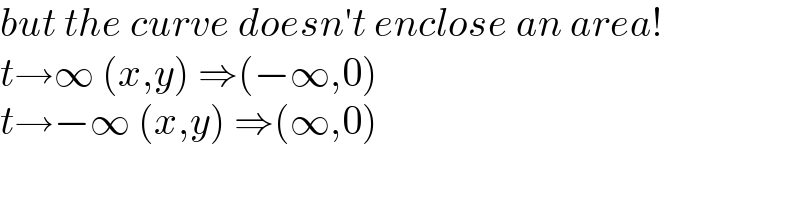
$${but}\:{the}\:{curve}\:{doesn}'{t}\:{enclose}\:{an}\:{area}! \\ $$$${t}\rightarrow\infty\:\left({x},{y}\right)\:\Rightarrow\left(−\infty,\mathrm{0}\right) \\ $$$${t}\rightarrow−\infty\:\left({x},{y}\right)\:\Rightarrow\left(\infty,\mathrm{0}\right) \\ $$
Commented by mr W last updated on 11/Dec/22

Commented by Frix last updated on 11/Dec/22

$$\mathrm{It}'\mathrm{s}\:\mathrm{one}\:\mathrm{of}\:\mathrm{these}\:\mathrm{questions}\:\mathrm{where}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to} \\ $$$$\mathrm{guess}\:\mathrm{what}'\mathrm{s}\:{really}\:\mathrm{meant}.\:\mathrm{If}\:{t}^{\mathrm{3}} \:\mathrm{is}\:{really} \\ $$$${t}^{\mathrm{2}} \:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{the}\:\mathrm{answer}\:\pi. \\ $$
