Question Number 182508 by peter frank last updated on 10/Dec/22

Answered by mahdipoor last updated on 10/Dec/22
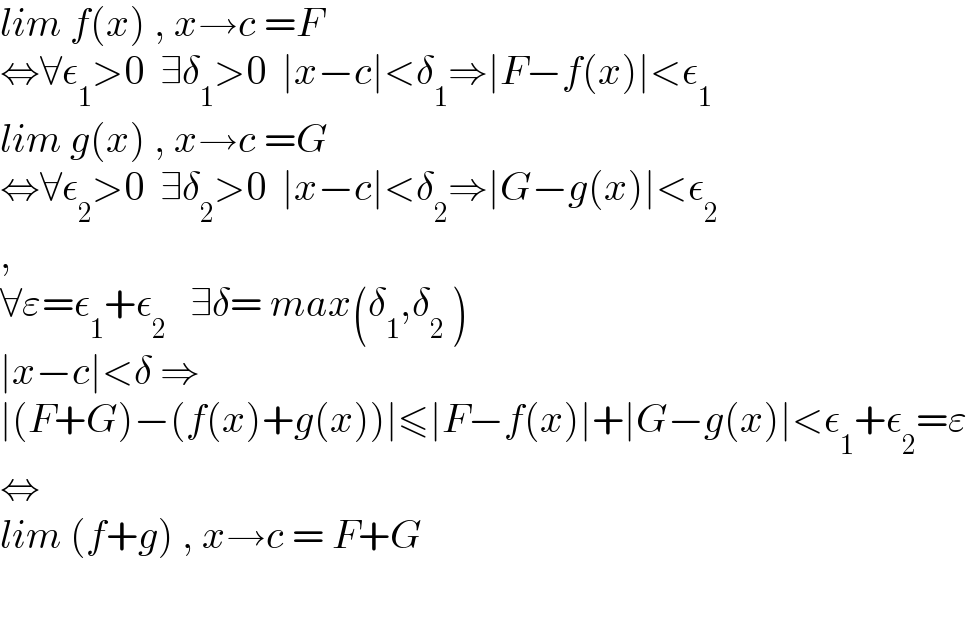
$${lim}\:{f}\left({x}\right)\:,\:{x}\rightarrow{c}\:={F} \\ $$$$\Leftrightarrow\forall\epsilon_{\mathrm{1}} >\mathrm{0}\:\:\exists\delta_{\mathrm{1}} >\mathrm{0}\:\:\mid{x}−{c}\mid<\delta_{\mathrm{1}} \Rightarrow\mid{F}−{f}\left({x}\right)\mid<\epsilon_{\mathrm{1}} \\ $$$${lim}\:{g}\left({x}\right)\:,\:{x}\rightarrow{c}\:={G} \\ $$$$\Leftrightarrow\forall\epsilon_{\mathrm{2}} >\mathrm{0}\:\:\exists\delta_{\mathrm{2}} >\mathrm{0}\:\:\mid{x}−{c}\mid<\delta_{\mathrm{2}} \Rightarrow\mid{G}−{g}\left({x}\right)\mid<\epsilon_{\mathrm{2}} \\ $$$$, \\ $$$$\forall\varepsilon=\epsilon_{\mathrm{1}} +\epsilon_{\mathrm{2}} \:\:\:\exists\delta=\:{max}\left(\delta_{\mathrm{1}} ,\delta_{\mathrm{2}} \:\right) \\ $$$$\mid{x}−{c}\mid<\delta\:\Rightarrow \\ $$$$\mid\left({F}+{G}\right)−\left({f}\left({x}\right)+{g}\left({x}\right)\right)\mid\leqslant\mid{F}−{f}\left({x}\right)\mid+\mid{G}−{g}\left({x}\right)\mid<\epsilon_{\mathrm{1}} +\epsilon_{\mathrm{2}} =\varepsilon \\ $$$$\Leftrightarrow \\ $$$${lim}\:\left({f}+{g}\right)\:,\:{x}\rightarrow{c}\:=\:{F}+{G} \\ $$$$ \\ $$
