Question Number 182542 by cortano1 last updated on 11/Dec/22
Commented by cortano1 last updated on 11/Dec/22

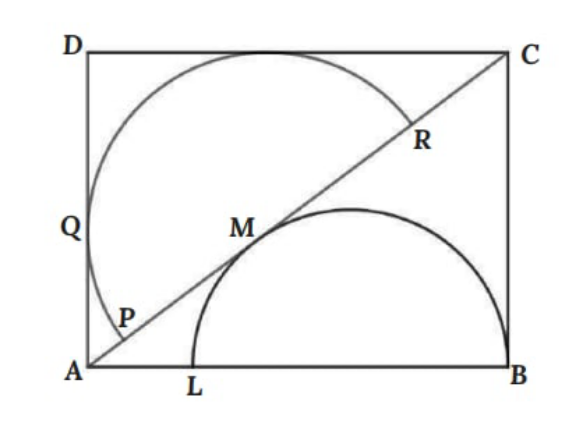
$$\mathrm{Radius}\:\mathrm{semi}\:\mathrm{circle}\:\mathrm{PQR}\:=\:\mathrm{24}\:\mathrm{cm} \\ $$$$\mathrm{radius}\:\mathrm{semi}\:\mathrm{circle}\:\mathrm{BML}\:=\:\mathrm{21cm} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{ABCD}\:. \\ $$
Answered by mr W last updated on 11/Dec/22
Commented by mr W last updated on 11/Dec/22
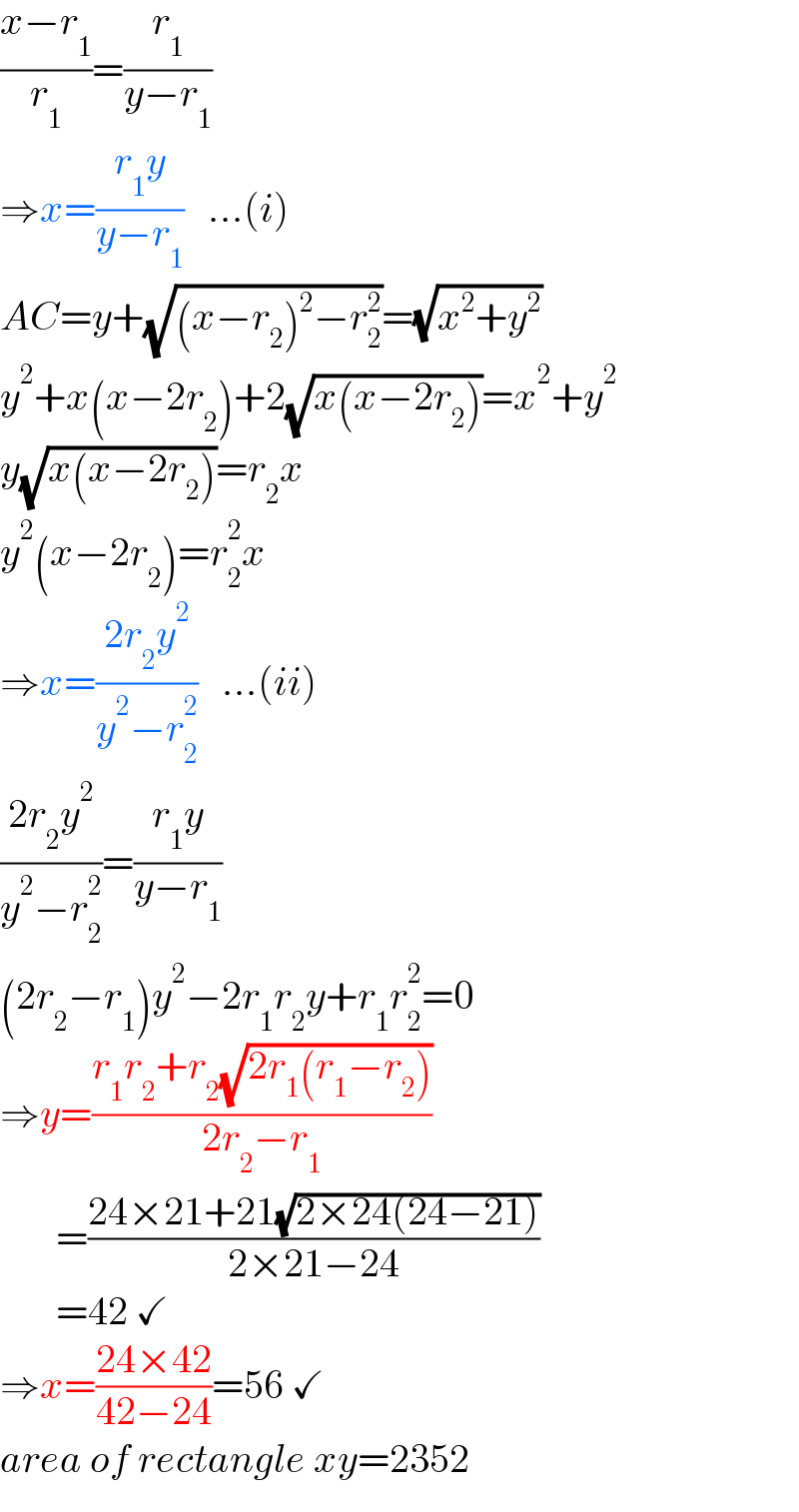
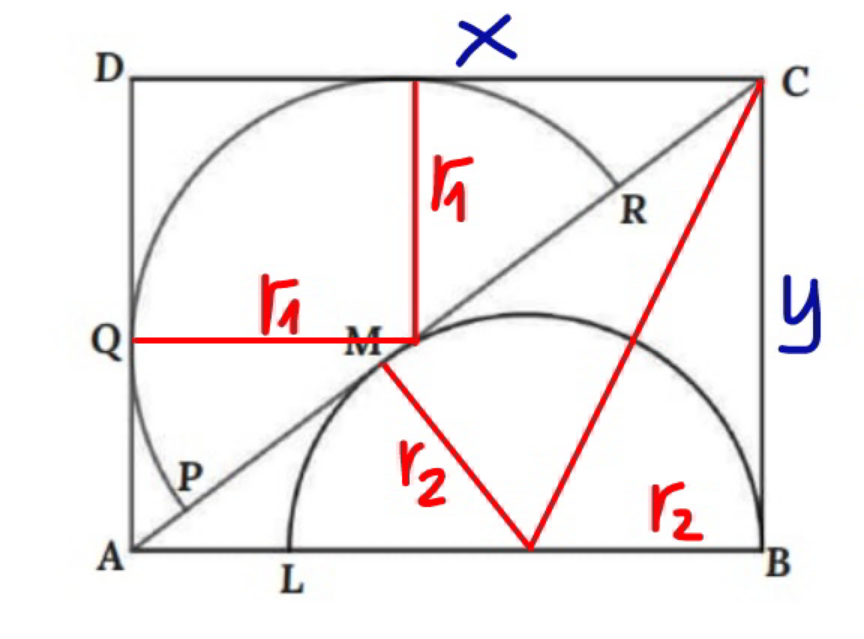
$$\frac{{x}−{r}_{\mathrm{1}} }{{r}_{\mathrm{1}} }=\frac{{r}_{\mathrm{1}} }{{y}−{r}_{\mathrm{1}} } \\ $$$$\Rightarrow{x}=\frac{{r}_{\mathrm{1}} {y}}{{y}−{r}_{\mathrm{1}} }\:\:\:…\left({i}\right) \\ $$$${AC}={y}+\sqrt{\left({x}−{r}_{\mathrm{2}} \right)^{\mathrm{2}} −{r}_{\mathrm{2}} ^{\mathrm{2}} }=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} +{x}\left({x}−\mathrm{2}{r}_{\mathrm{2}} \right)+\mathrm{2}\sqrt{{x}\left({x}−\mathrm{2}{r}_{\mathrm{2}} \right)}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${y}\sqrt{{x}\left({x}−\mathrm{2}{r}_{\mathrm{2}} \right)}={r}_{\mathrm{2}} {x} \\ $$$${y}^{\mathrm{2}} \left({x}−\mathrm{2}{r}_{\mathrm{2}} \right)={r}_{\mathrm{2}} ^{\mathrm{2}} {x} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}{r}_{\mathrm{2}} {y}^{\mathrm{2}} }{{y}^{\mathrm{2}} −{r}_{\mathrm{2}} ^{\mathrm{2}} }\:\:\:…\left({ii}\right) \\ $$$$\frac{\mathrm{2}{r}_{\mathrm{2}} {y}^{\mathrm{2}} }{{y}^{\mathrm{2}} −{r}_{\mathrm{2}} ^{\mathrm{2}} }=\frac{{r}_{\mathrm{1}} {y}}{{y}−{r}_{\mathrm{1}} }\: \\ $$$$\left(\mathrm{2}{r}_{\mathrm{2}} −{r}_{\mathrm{1}} \right){y}^{\mathrm{2}} −\mathrm{2}{r}_{\mathrm{1}} {r}_{\mathrm{2}} {y}+{r}_{\mathrm{1}} {r}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{y}=\frac{{r}_{\mathrm{1}} {r}_{\mathrm{2}} +{r}_{\mathrm{2}} \sqrt{\mathrm{2}{r}_{\mathrm{1}} \left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} \right)}}{\mathrm{2}{r}_{\mathrm{2}} −{r}_{\mathrm{1}} } \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{24}×\mathrm{21}+\mathrm{21}\sqrt{\mathrm{2}×\mathrm{24}\left(\mathrm{24}−\mathrm{21}\right)}}{\mathrm{2}×\mathrm{21}−\mathrm{24}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{42}\:\checkmark \\ $$$$\Rightarrow{x}=\frac{\mathrm{24}×\mathrm{42}}{\mathrm{42}−\mathrm{24}}=\mathrm{56}\:\checkmark \\ $$$${area}\:{of}\:{rectangle}\:{xy}=\mathrm{2352} \\ $$
Commented by cortano1 last updated on 11/Dec/22

$$\mathrm{nice}… \\ $$$$ \\ $$
Commented by EpicMaths last updated on 11/Dec/22

$$ \\ $$
Commented by Rasheed.Sindhi last updated on 12/Dec/22
$${Something}\:{is}\:{written}\:{in}\:{white}\:{ink}! \\ $$
