Question Number 182675 by Acem last updated on 12/Dec/22

Answered by HeferH last updated on 12/Dec/22

$$\mathrm{64}?\: \\ $$
Commented by Acem last updated on 12/Dec/22

$$\:{yes}! \\ $$
Answered by HeferH last updated on 12/Dec/22
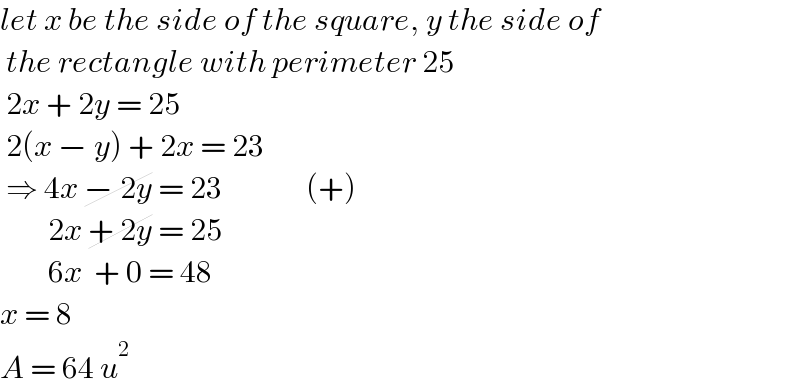
$${let}\:{x}\:{be}\:{the}\:{side}\:{of}\:{the}\:{square},\:{y}\:{the}\:{side}\:{of}\: \\ $$$$\:{the}\:{rectangle}\:{with}\:{perimeter}\:\mathrm{25} \\ $$$$\:\mathrm{2}{x}\:+\:\mathrm{2}{y}\:=\:\mathrm{25} \\ $$$$\:\mathrm{2}\left({x}\:−\:{y}\right)\:+\:\mathrm{2}{x}\:=\:\mathrm{23} \\ $$$$\:\Rightarrow\:\mathrm{4}{x}\:\cancel{−\:\mathrm{2}{y}}\:=\:\mathrm{23}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(+\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}{x}\:\cancel{+\:\mathrm{2}{y}}\:=\:\mathrm{25}\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{6}{x}\:\:+\:\mathrm{0}\:=\:\mathrm{48} \\ $$$${x}\:=\:\mathrm{8}\: \\ $$$${A}\:=\:\mathrm{64}\:{u}^{\mathrm{2}} \\ $$
Commented by Acem last updated on 13/Dec/22

$${Thank}\:{you}\:{Sir}! \\ $$
