Question Number 182676 by yaslm last updated on 12/Dec/22

Answered by Acem last updated on 12/Dec/22
![If we consider that the sequare isn′t a special case of the rectangle, then the required rectangles are: ]0, 1[ ∪ ]1, +∞[_(ℓ) × 1_(w) ⇔ R^(+★, +1) _(ℓ) × 1_(w)](https://www.tinkutara.com/question/Q182677.png)
$${If}\:{we}\:{consider}\:{that}\:{the}\:{sequare}\:{isn}'{t}\:{a}\:{special} \\ $$$$\:{case}\:{of}\:{the}\:{rectangle},\:{then}\:{the}\:{required}\:{rectangles} \\ $$$$\left.\:{are}:\:\underset{\ell} {\underbrace{\right]\mathrm{0},\:\mathrm{1}\left[\:\cup\:\right]\mathrm{1},\:+\infty\left[}}\:×\:\underset{{w}} {\underbrace{\mathrm{1}}}\:\:\:\:\Leftrightarrow\:\:\:\:\underset{\ell} {\underbrace{\mathbb{R}^{+\bigstar,\:+\mathrm{1}} }}\:×\:\underset{{w}} {\underbrace{\mathrm{1}}}\right. \\ $$
Answered by TheSupreme last updated on 14/Dec/22
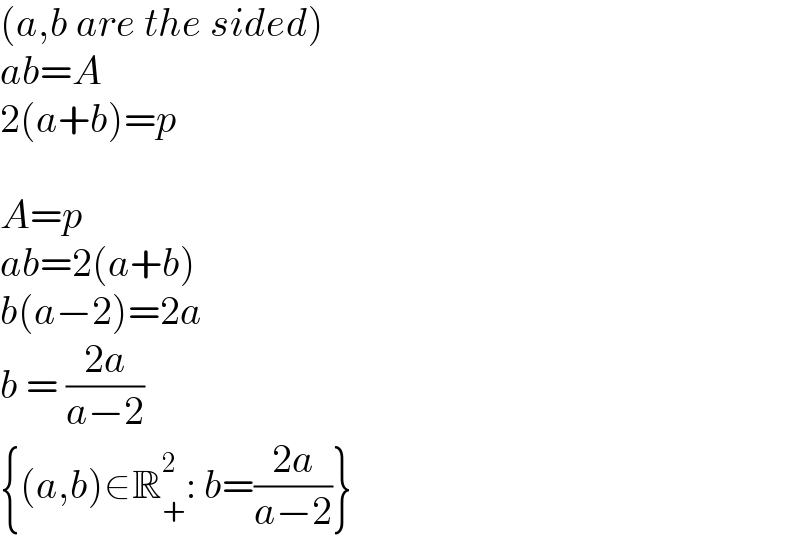
$$\left({a},{b}\:{are}\:{the}\:{sided}\right) \\ $$$${ab}={A} \\ $$$$\mathrm{2}\left({a}+{b}\right)={p} \\ $$$$ \\ $$$${A}={p} \\ $$$${ab}=\mathrm{2}\left({a}+{b}\right) \\ $$$${b}\left({a}−\mathrm{2}\right)=\mathrm{2}{a} \\ $$$${b}\:=\:\frac{\mathrm{2}{a}}{{a}−\mathrm{2}} \\ $$$$\left\{\left({a},{b}\right)\in\mathbb{R}_{+} ^{\mathrm{2}} :\:{b}=\frac{\mathrm{2}{a}}{{a}−\mathrm{2}}\right\} \\ $$
