Question Number 182737 by cortano1 last updated on 13/Dec/22

Answered by dre23 last updated on 14/Dec/22
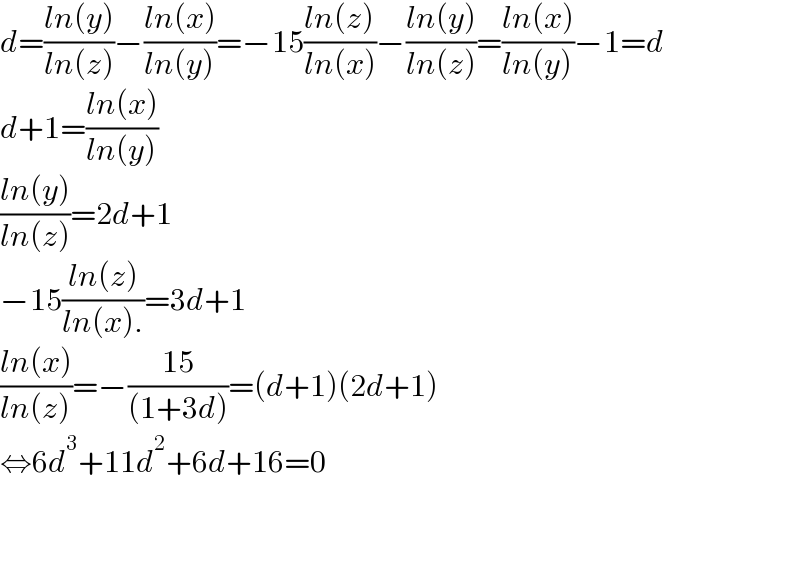
$${d}=\frac{{ln}\left({y}\right)}{{ln}\left({z}\right)}−\frac{{ln}\left({x}\right)}{{ln}\left({y}\right)}=−\mathrm{15}\frac{{ln}\left({z}\right)}{{ln}\left({x}\right)}−\frac{{ln}\left({y}\right)}{{ln}\left({z}\right)}=\frac{{ln}\left({x}\right)}{{ln}\left({y}\right)}−\mathrm{1}={d} \\ $$$${d}+\mathrm{1}=\frac{{ln}\left({x}\right)}{{ln}\left({y}\right)} \\ $$$$\frac{{ln}\left({y}\right)}{{ln}\left({z}\right)}=\mathrm{2}{d}+\mathrm{1} \\ $$$$−\mathrm{15}\frac{{ln}\left({z}\right)}{{ln}\left({x}\right).}=\mathrm{3}{d}+\mathrm{1} \\ $$$$\frac{{ln}\left({x}\right)}{{ln}\left({z}\right)}=−\frac{\mathrm{15}}{\left(\mathrm{1}+\mathrm{3}{d}\right)}=\left({d}+\mathrm{1}\right)\left(\mathrm{2}{d}+\mathrm{1}\right) \\ $$$$\Leftrightarrow\mathrm{6}{d}^{\mathrm{3}} +\mathrm{11}{d}^{\mathrm{2}} +\mathrm{6}{d}+\mathrm{16}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
