Question Number 18278 by mondodotto@gmail.com last updated on 17/Jul/17
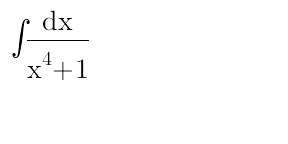
Commented by mondodotto@gmail.com last updated on 18/Jul/17

$$\mathrm{help}\:\mathrm{please}!! \\ $$
Answered by geovane10math last updated on 18/Jul/17

$$\mathrm{Put}\:\mathrm{it}\:\mathrm{in}\:\mathrm{Wolfram}\:\mathrm{Alpha}… \\ $$
Answered by ajfour last updated on 18/Jul/17
![∫(((1/x^2 )dx)/(x^2 +(1/x^2 )))=(1/2)∫(((1+(1/x^2 ))−(1−(1/x^2 )))/(x^2 +(1/x^2 )))dx =∫(((1+(1/x^2 ))dx)/((x−(1/x))^2 +2))−∫(((1−(1/x^2 ))dx)/((x+(1/x))^2 −2)) =(1/( (√2)))tan^(−1) (((x−1/x)/( (√2))))−(1/( (√2)))tan^(−1) (((x+1/x)/( (√2))))+C =(1/( (√2)))[tan^(−1) (((x^2 −1)/(x(√2))))−tan^(−1) (((x^2 +1)/(x(√2))))]+C .](https://www.tinkutara.com/question/Q18312.png)
$$\int\frac{\left(\mathrm{1}/\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\left(\mathrm{1}/\mathrm{x}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}\mathrm{dx} \\ $$$$=\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{2}}−\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}−\mathrm{1}/\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\mathrm{1}/\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{2}}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{2}}}\right)\right]+\mathrm{C}\:. \\ $$
