Question Number 182896 by sciencestudent last updated on 16/Dec/22

Commented by JDamian last updated on 16/Dec/22
bigger than what?
Answered by mr W last updated on 17/Dec/22
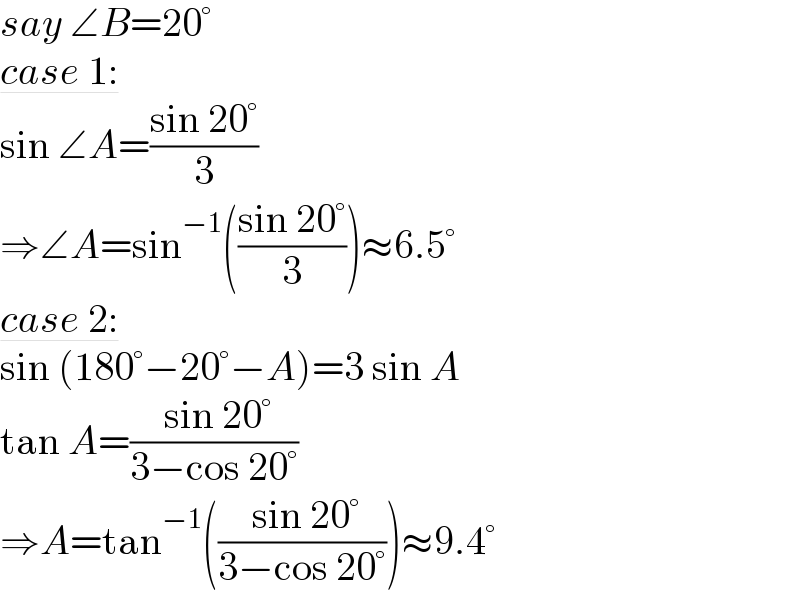
$${say}\:\angle{B}=\mathrm{20}° \\ $$$$\underline{{case}\:\mathrm{1}:} \\ $$$$\mathrm{sin}\:\angle{A}=\frac{\mathrm{sin}\:\mathrm{20}°}{\mathrm{3}} \\ $$$$\Rightarrow\angle{A}=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\mathrm{20}°}{\mathrm{3}}\right)\approx\mathrm{6}.\mathrm{5}° \\ $$$$\underline{{case}\:\mathrm{2}:} \\ $$$$\mathrm{sin}\:\left(\mathrm{180}°−\mathrm{20}°−{A}\right)=\mathrm{3}\:\mathrm{sin}\:{A} \\ $$$$\mathrm{tan}\:{A}=\frac{\:\mathrm{sin}\:\mathrm{20}°}{\mathrm{3}−\mathrm{cos}\:\mathrm{20}°} \\ $$$$\Rightarrow{A}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\:\mathrm{sin}\:\mathrm{20}°}{\mathrm{3}−\mathrm{cos}\:\mathrm{20}°}\right)\approx\mathrm{9}.\mathrm{4}° \\ $$
Commented by mr W last updated on 17/Dec/22
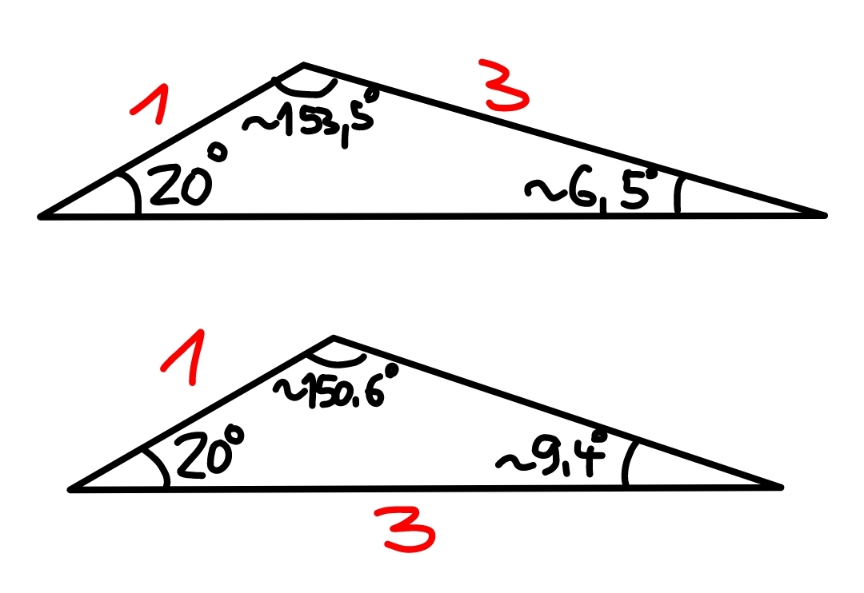
Commented by sciencestudent last updated on 18/Dec/22

$${thanks}\:{sir}! \\ $$
