Menu Close

Question-182973

Tinku Tara 0 Comments
Pin




Question Number 182973 by HeferH last updated on 17/Dec/22
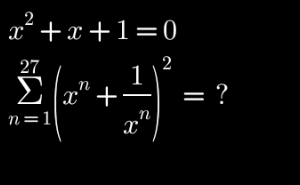
Answered by Rasheed.Sindhi last updated on 18/Dec/22
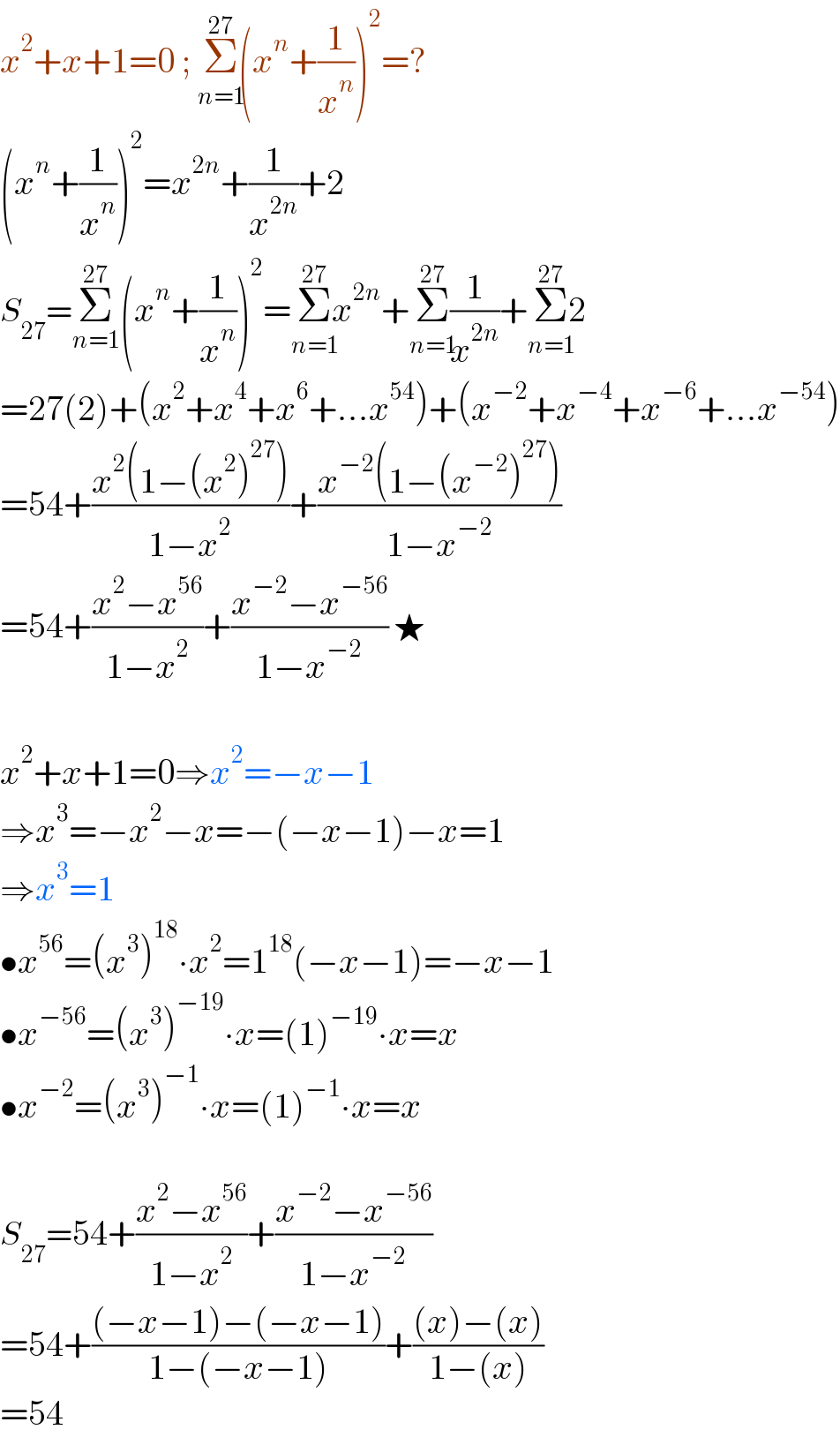
x^2 +x+1=0 ; Σ_(n=1) ^(27) (x^n +(1/x^n ))^2 =? (x^n +(1/x^n ))^2 =x^(2n) +(1/x^(2n) )+2 S_(27) =Σ_(n=1) ^(27) (x^n +(1/x^n ))^2 =Σ_(n=1) ^(27) x^(2n) +Σ_(n=1) ^(27) (1/x^(2n) )+Σ_(n=1) ^(27) 2 =27(2)+(x^2 +x^4 +x^6 +...x^(54) )+(x^(−2) +x^(−4) +x^(−6) +...x^(−54) ) =54+((x^2 (1−(x^2 )^(27) ))/(1−x^2 ))+((x^(−2) (1−(x^(−2) )^(27) ))/(1−x^(−2) )) =54+((x^2 −x^(56) )/(1−x^2 ))+((x^(−2) −x^(−56) )/(1−x^(−2) )) ★ x^2 +x+1=0⇒x^2 =−x−1 ⇒x^3 =−x^2 −x=−(−x−1)−x=1 ⇒x^3 =1 •x^(56) =(x^3 )^(18) ∙x^2 =1^(18) (−x−1)=−x−1 •x^(−56) =(x^3 )^(−19) ∙x=(1)^(−19) ∙x=x •x^(−2) =(x^3 )^(−1) ∙x=(1)^(−1) ∙x=x S_(27) =54+((x^2 −x^(56) )/(1−x^2 ))+((x^(−2) −x^(−56) )/(1−x^(−2) )) =54+(((−x−1)−(−x−1))/(1−(−x−1)))+(((x)−(x))/(1−(x))) =54
$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\:;\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{27}} {\Sigma}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{\mathrm{2}} =? \\ $$$$\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{\mathrm{2}} ={x}^{\mathrm{2}{n}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }+\mathrm{2} \\ $$$${S}_{\mathrm{27}} =\underset{{n}=\mathrm{1}} {\overset{\mathrm{27}} {\sum}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{\mathrm{2}} =\underset{{n}=\mathrm{1}} {\overset{\mathrm{27}} {\Sigma}}{x}^{\mathrm{2}{n}} +\underset{{n}=\mathrm{1}} {\overset{\mathrm{27}} {\Sigma}}\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }+\underset{{n}=\mathrm{1}} {\overset{\mathrm{27}} {\Sigma}}\mathrm{2} \\ $$$$=\mathrm{27}\left(\mathrm{2}\right)+\left({x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{6}} +…{x}^{\mathrm{54}} \right)+\left({x}^{−\mathrm{2}} +{x}^{−\mathrm{4}} +{x}^{−\mathrm{6}} +…{x}^{−\mathrm{54}} \right) \\ $$$$=\mathrm{54}+\frac{{x}^{\mathrm{2}} \left(\mathrm{1}−\left({x}^{\mathrm{2}} \right)^{\mathrm{27}} \right)}{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{{x}^{−\mathrm{2}} \left(\mathrm{1}−\left({x}^{−\mathrm{2}} \right)^{\mathrm{27}} \right)}{\mathrm{1}−{x}^{−\mathrm{2}} } \\ $$$$=\mathrm{54}+\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{56}} }{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{{x}^{−\mathrm{2}} −{x}^{−\mathrm{56}} }{\mathrm{1}−{x}^{−\mathrm{2}} }\:\bigstar \\ $$$$\: \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}^{\mathrm{2}} =−{x}−\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{3}} =−{x}^{\mathrm{2}} −{x}=−\left(−{x}−\mathrm{1}\right)−{x}=\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{3}} =\mathrm{1} \\ $$$$\bullet{x}^{\mathrm{56}} =\left({x}^{\mathrm{3}} \right)^{\mathrm{18}} \centerdot{x}^{\mathrm{2}} =\mathrm{1}^{\mathrm{18}} \left(−{x}−\mathrm{1}\right)=−{x}−\mathrm{1} \\ $$$$\bullet{x}^{−\mathrm{56}} =\left({x}^{\mathrm{3}} \right)^{−\mathrm{19}} \centerdot{x}=\left(\mathrm{1}\right)^{−\mathrm{19}} \centerdot{x}={x} \\ $$$$\bullet{x}^{−\mathrm{2}} =\left({x}^{\mathrm{3}} \right)^{−\mathrm{1}} \centerdot{x}=\left(\mathrm{1}\right)^{−\mathrm{1}} \centerdot{x}={x} \\ $$$$\: \\ $$$${S}_{\mathrm{27}} =\mathrm{54}+\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{56}} }{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{{x}^{−\mathrm{2}} −{x}^{−\mathrm{56}} }{\mathrm{1}−{x}^{−\mathrm{2}} } \\ $$$$=\mathrm{54}+\frac{\left(−{x}−\mathrm{1}\right)−\left(−{x}−\mathrm{1}\right)}{\mathrm{1}−\left(−{x}−\mathrm{1}\right)}+\frac{\left({x}\right)−\left({x}\right)}{\mathrm{1}−\left({x}\right)} \\ $$$$=\mathrm{54} \\ $$
Commented by Rasheed.Sindhi last updated on 18/Dec/22
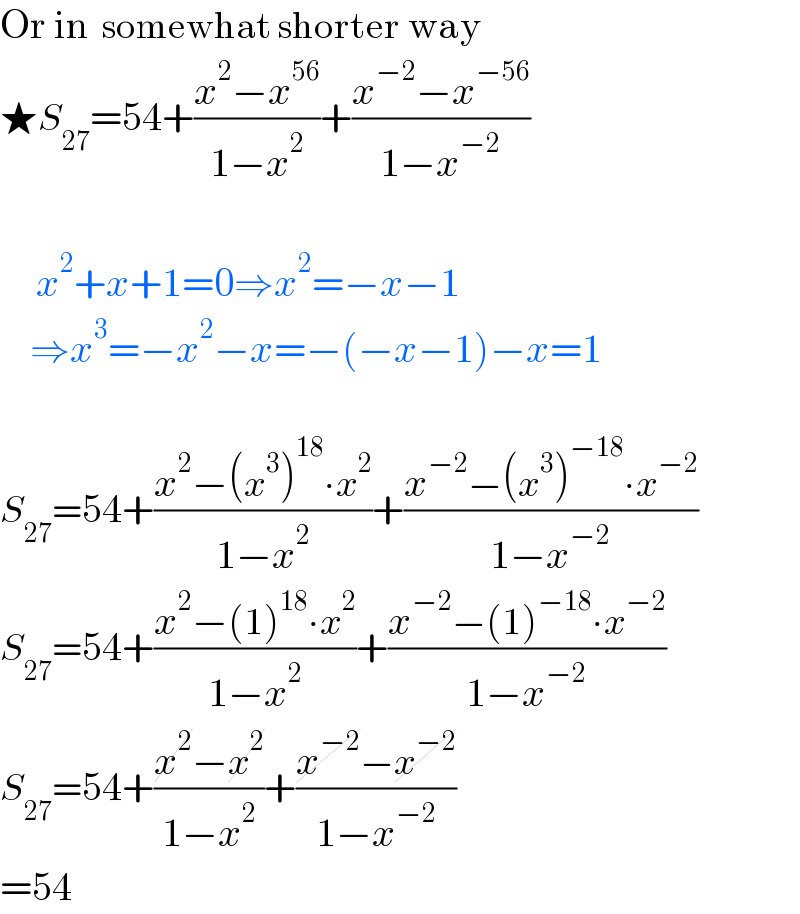
Or in somewhat shorter way ★S_(27) =54+((x^2 −x^(56) )/(1−x^2 ))+((x^(−2) −x^(−56) )/(1−x^(−2) )) x^2 +x+1=0⇒x^2 =−x−1 ⇒x^3 =−x^2 −x=−(−x−1)−x=1 S_(27) =54+((x^2 −(x^3 )^(18) ∙x^2 )/(1−x^2 ))+((x^(−2) −(x^3 )^(−18) ∙x^(−2) )/(1−x^(−2) )) S_(27) =54+((x^2 −(1)^(18) ∙x^2 )/(1−x^2 ))+((x^(−2) −(1)^(−18) ∙x^(−2) )/(1−x^(−2) )) S_(27) =54+((x^2 −x^2 )/(1−x^2 ))+((x^(−2) −x^(−2) )/(1−x^(−2) )) =54
$$\mathrm{Or}\:\mathrm{in}\:\:\mathrm{somewhat}\:\mathrm{shorter}\:\mathrm{way} \\ $$$$\bigstar{S}_{\mathrm{27}} =\mathrm{54}+\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{56}} }{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{{x}^{−\mathrm{2}} −{x}^{−\mathrm{56}} }{\mathrm{1}−{x}^{−\mathrm{2}} } \\ $$$$\: \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}^{\mathrm{2}} =−{x}−\mathrm{1} \\ $$$$\:\:\:\:\:\Rightarrow{x}^{\mathrm{3}} =−{x}^{\mathrm{2}} −{x}=−\left(−{x}−\mathrm{1}\right)−{x}=\mathrm{1} \\ $$$$\: \\ $$$${S}_{\mathrm{27}} =\mathrm{54}+\frac{{x}^{\mathrm{2}} −\left({x}^{\mathrm{3}} \right)^{\mathrm{18}} \centerdot{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{{x}^{−\mathrm{2}} −\left({x}^{\mathrm{3}} \right)^{−\mathrm{18}} \centerdot{x}^{−\mathrm{2}} }{\mathrm{1}−{x}^{−\mathrm{2}} } \\ $$$${S}_{\mathrm{27}} =\mathrm{54}+\frac{{x}^{\mathrm{2}} −\left(\mathrm{1}\right)^{\mathrm{18}} \centerdot{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{{x}^{−\mathrm{2}} −\left(\mathrm{1}\right)^{−\mathrm{18}} \centerdot{x}^{−\mathrm{2}} }{\mathrm{1}−{x}^{−\mathrm{2}} } \\ $$$${S}_{\mathrm{27}} =\mathrm{54}+\frac{\cancel{{x}^{\mathrm{2}} }−\cancel{{x}^{\mathrm{2}} }}{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{\cancel{{x}^{−\mathrm{2}} }−\cancel{{x}^{−\mathrm{2}} }}{\mathrm{1}−{x}^{−\mathrm{2}} } \\ $$$$=\mathrm{54} \\ $$
Answered by TANMAY PANACEA last updated on 18/Dec/22
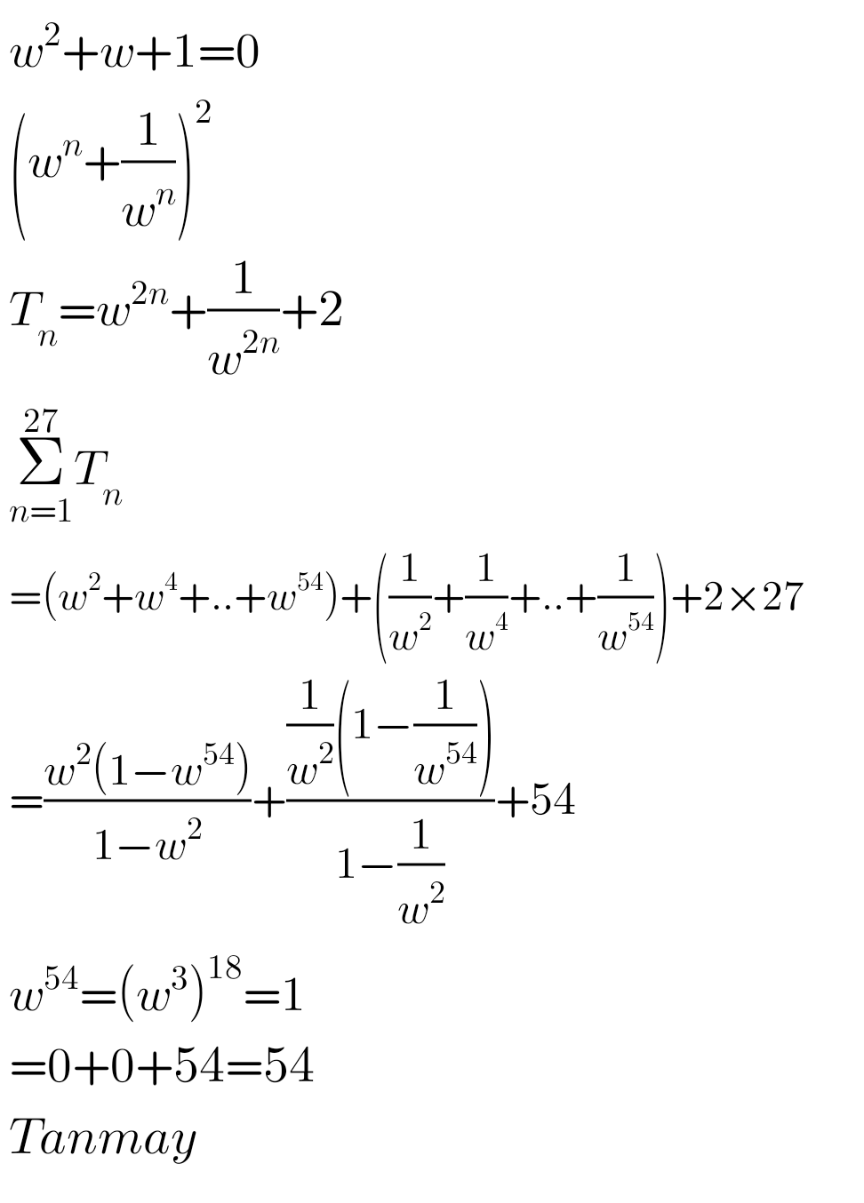
Commented by mr W last updated on 18/Dec/22
welcome back sir! you seem to have taken a long break.
$${welcome}\:{back}\:{sir}! \\ $$$${you}\:{seem}\:{to}\:{have}\:{taken}\:{a}\:{long}\:{break}. \\ $$
Commented by Rasheed.Sindhi last updated on 18/Dec/22
Tanmay sir, happy to see you again!
$$\mathcal{T}{anmay}\:{sir},\:{happy}\:{to}\:{see}\:{you}\:{again}! \\ $$
Answered by TheSupreme last updated on 18/Dec/22
x+1+(1/x)=0 →(1/x)=−x−1 Σ_(n=1) ^(27) x^(2n) +(1/x^(2n) )+2= =((1−x^(2∗27−1) )/(1−x))−1+((1−(1/x^(2∗27−1) ))/(1−(1/x)))−1+2∙27= =((1−x^(53) )/(1−x))−((1−x^(53) )/(x^(52) (1−x)))+52 =((1−x^(53) )/(1−x))[1−(1/x^(52) )]+52= = x^2 +x+1=0→x_(1,2) =((−1±(√(−3)))/2)=e^(±(π/3)i) Σ(e^(k(π/3)i) +e^(−k(π/3)i) )^2 =Σ4cos^2 (k(π/3))= =Σ_(n=1) ^9 4cos^2 (0)+4cos^2 ((π/3))+4cos^2 ((2π)/3)= =4Σ_(n=1) ^9 1+(1/4)+(1/4)=6∙9 =54
$${x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}=\mathrm{0}\:\rightarrow\frac{\mathrm{1}}{{x}}=−{x}−\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{27}} {\sum}}{x}^{\mathrm{2}{n}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }+\mathrm{2}= \\ $$$$=\frac{\mathrm{1}−{x}^{\mathrm{2}\ast\mathrm{27}−\mathrm{1}} }{\mathrm{1}−{x}}−\mathrm{1}+\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}\ast\mathrm{27}−\mathrm{1}} }}{\mathrm{1}−\frac{\mathrm{1}}{{x}}}−\mathrm{1}+\mathrm{2}\centerdot\mathrm{27}= \\ $$$$=\frac{\mathrm{1}−{x}^{\mathrm{53}} }{\mathrm{1}−{x}}−\frac{\mathrm{1}−{x}^{\mathrm{53}} }{{x}^{\mathrm{52}} \left(\mathrm{1}−{x}\right)}+\mathrm{52} \\ $$$$=\frac{\mathrm{1}−{x}^{\mathrm{53}} }{\mathrm{1}−{x}}\left[\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{52}} }\right]+\mathrm{52}= \\ $$$$= \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\rightarrow{x}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{1}\pm\sqrt{−\mathrm{3}}}{\mathrm{2}}={e}^{\pm\frac{\pi}{\mathrm{3}}{i}} \: \\ $$$$\Sigma\left({e}^{{k}\frac{\pi}{\mathrm{3}}{i}} +{e}^{−{k}\frac{\pi}{\mathrm{3}}{i}} \right)^{\mathrm{2}} =\Sigma\mathrm{4}{cos}^{\mathrm{2}} \left({k}\frac{\pi}{\mathrm{3}}\right)= \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\mathrm{4}{cos}^{\mathrm{2}} \left(\mathrm{0}\right)+\mathrm{4}{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{3}}\right)+\mathrm{4}{cos}^{\mathrm{2}} \frac{\mathrm{2}\pi}{\mathrm{3}}= \\ $$$$=\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{6}\centerdot\mathrm{9}\:=\mathrm{54} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *