Question Number 183076 by Engr_Jidda last updated on 19/Dec/22

Answered by TheSupreme last updated on 21/Dec/22
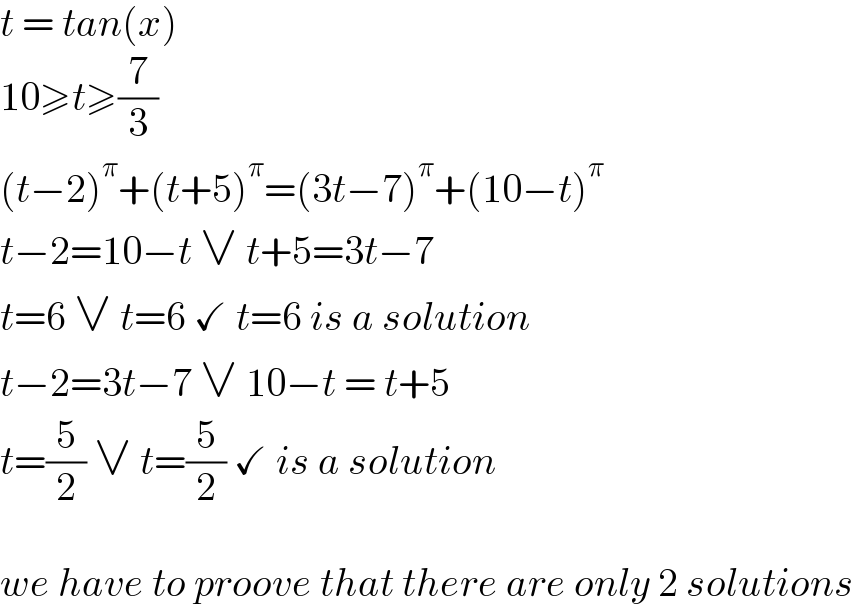
$${t}\:=\:{tan}\left({x}\right) \\ $$$$\mathrm{10}\geqslant{t}\geqslant\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\left({t}−\mathrm{2}\right)^{\pi} +\left({t}+\mathrm{5}\right)^{\pi} =\left(\mathrm{3}{t}−\mathrm{7}\right)^{\pi} +\left(\mathrm{10}−{t}\right)^{\pi} \\ $$$${t}−\mathrm{2}=\mathrm{10}−{t}\:\vee\:{t}+\mathrm{5}=\mathrm{3}{t}−\mathrm{7} \\ $$$${t}=\mathrm{6}\:\vee\:{t}=\mathrm{6}\:\checkmark\:{t}=\mathrm{6}\:{is}\:{a}\:{solution} \\ $$$${t}−\mathrm{2}=\mathrm{3}{t}−\mathrm{7}\:\vee\:\mathrm{10}−{t}\:=\:{t}+\mathrm{5} \\ $$$${t}=\frac{\mathrm{5}}{\mathrm{2}}\:\vee\:{t}=\frac{\mathrm{5}}{\mathrm{2}}\:\checkmark\:{is}\:{a}\:{solution} \\ $$$$ \\ $$$${we}\:{have}\:{to}\:{proove}\:{that}\:{there}\:{are}\:{only}\:\mathrm{2}\:{solutions} \\ $$
