Menu Close

Question-183084

Tinku Tara 0 Comments
Pin




Question Number 183084 by Rasheed.Sindhi last updated on 19/Dec/22
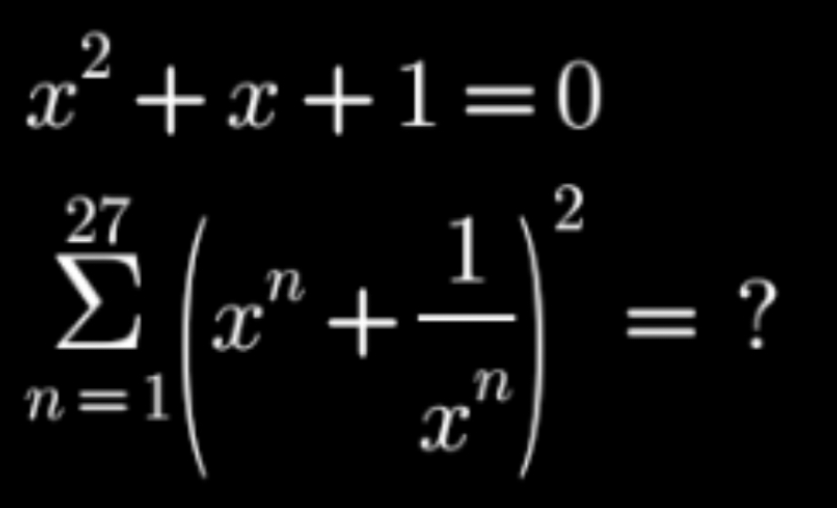
Commented by JDamian last updated on 19/Dec/22
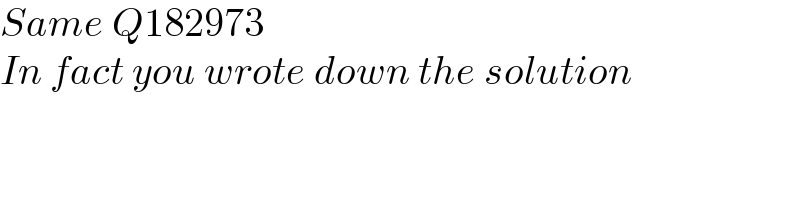
Same Q182973 In fact you wrote down the solution
$${Same}\:{Q}\mathrm{182973} \\ $$$${In}\:{fact}\:{you}\:{wrote}\:{down}\:{the}\:{solution} \\ $$
Commented by Rasheed.Sindhi last updated on 19/Dec/22
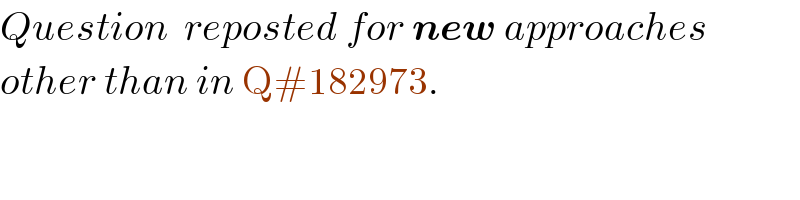
Question reposted for new approaches other than in Q#182973.
$${Question}\:\:{reposted}\:{for}\:\boldsymbol{{new}}\:{approaches} \\ $$$${other}\:{than}\:{in}\:\mathrm{Q}#\mathrm{182973}. \\ $$
Commented by Rasheed.Sindhi last updated on 19/Dec/22
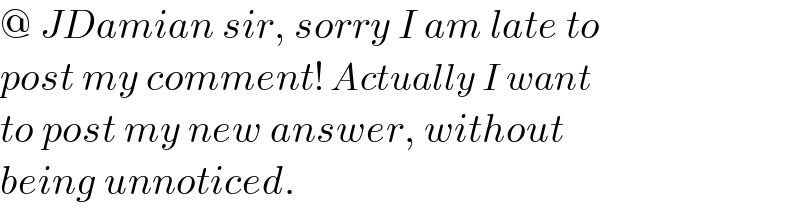
@ JDamian sir, sorry I am late to post my comment! Actually I want to post my new answer, without being unnoticed.
$$@\:{JDamian}\:{sir},\:{sorry}\:{I}\:{am}\:{late}\:{to} \\ $$$${post}\:{my}\:{comment}!\:{Actually}\:{I}\:{want} \\ $$$${to}\:{post}\:{my}\:{new}\:{answer},\:{without} \\ $$$${being}\:{unnoticed}. \\ $$
Answered by Rasheed.Sindhi last updated on 20/Dec/22
x^2 +x+1=0; Σ_(n=1) ^(27) (x^n +(1/x^n ))^2 =? x^2 +x+1=0_(⇓) • determinant (((x^2 =−x−1))) ⇒x^3 =−x^2 −x=−(−x−1)−x=1⇒ • determinant (((x^3 =1))) • determinant (((x^2 +1=−x))) • determinant (((x+1=−x^2 ))) determinant (((Σ_(n=1) ^(27) (x^n +(1/x^n ))^2 _( ^( _ _ _ ) =Σ_(n=1) ^9 {(x^(3n−2) +(1/x^(3n−2) ))^2 +(x^(3n−1) +(1/x^(3n−1) ))^2 +(x^(3n) +(1/x^(3n) ))^2 }) ))) =Σ_(n=1) ^9 {((x^3 )^n ∙x^(−2) +(1/((x^3 )^n ∙x^(−2) )))^2 +((x^3 )^n ∙x^(−1) +(1/((x^3 )^n ∙x^(−1) )))^2 +((x^3 )^n +(1/((x^3 )^n )))^2 } =Σ_(n=1) ^9 {((1)^n ∙x^(−2) +(1/((1)^n ∙x^(−2) )))^2 +((1)^n ∙x^(−2) +(1/((1)^n ∙x^(−2) )))^2 +((1)^n +(1/((1)^n )))^2 } =Σ_(n=1) ^9 {(x^(−2) +(1/x^(−2) ))^2 +(x^(−1) +(1/x^(−1) ))^2 +((1+(1/1))^2 } =Σ_(n=1) ^9 {(x^2 +(1/x^2 ))^2 +(x+(1/x))^2 +((2)^2 } =Σ_(n=1) ^9 {(((x^3 ∙x+1)/x^2 ))^2 +(((x^2 +1)/x))^2 +4} =Σ_(n=1) ^9 {(((x+1)/x^2 ))^2 +(((−x)/x))^2 +4} =Σ_(n=1) ^9 {(((−x^2 )/x^2 ))^2 +(((−x)/x))^2 +4} =Σ_(n=1) ^9 {(−1)^2 +(−1)^2 +4} =Σ_(n=1) ^9 (6)=6×9=54
$$ \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0};\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{27}} {\Sigma}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{\mathrm{2}} =? \\ $$$$\underset{\Downarrow} {\underbrace{{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}}} \\ $$$$\bullet\begin{array}{|c|}{{x}^{\mathrm{2}} =−{x}−\mathrm{1}}\\\hline\end{array} \\ $$$$\:\:\:\:\:\Rightarrow{x}^{\mathrm{3}} =−{x}^{\mathrm{2}} −{x}=−\left(−{x}−\mathrm{1}\right)−{x}=\mathrm{1}\Rightarrow \\ $$$$\bullet\begin{array}{|c|}{{x}^{\mathrm{3}} =\mathrm{1}}\\\hline\end{array}\:\: \\ $$$$\bullet\begin{array}{|c|}{{x}^{\mathrm{2}} +\mathrm{1}=−{x}}\\\hline\end{array} \\ $$$$\bullet\begin{array}{|c|}{{x}+\mathrm{1}=−{x}^{\mathrm{2}} }\\\hline\end{array}\: \\ $$$$\begin{array}{|c|}{\underset{\:\overset{\underset{\underset{\underset{\:} {\:}} {\:}} {\:}} {\:}\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left({x}^{\mathrm{3}{n}−\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}{n}−\mathrm{2}} }\right)^{\mathrm{2}} +\left({x}^{\mathrm{3}{n}−\mathrm{1}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}{n}−\mathrm{1}} }\right)^{\mathrm{2}} +\left({x}^{\mathrm{3}{n}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}{n}} }\right)^{\mathrm{2}} \right\}} {\underset{{n}=\mathrm{1}} {\overset{\mathrm{27}} {\sum}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{\mathrm{2}} }\:\:\:\:\:\:\:\:}\\\hline\end{array} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left(\left({x}^{\mathrm{3}} \right)^{{n}} \centerdot{x}^{−\mathrm{2}} +\frac{\mathrm{1}}{\left({x}^{\mathrm{3}} \right)^{{n}} \centerdot{x}^{−\mathrm{2}} }\right)^{\mathrm{2}} +\left(\left({x}^{\mathrm{3}} \right)^{{n}} \centerdot{x}^{−\mathrm{1}} +\frac{\mathrm{1}}{\left({x}^{\mathrm{3}} \right)^{{n}} \centerdot{x}^{−\mathrm{1}} }\right)^{\mathrm{2}} +\left(\left({x}^{\mathrm{3}} \right)^{{n}} +\frac{\mathrm{1}}{\left({x}^{\mathrm{3}} \right)^{{n}} }\right)^{\mathrm{2}} \right\} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left(\left(\mathrm{1}\right)^{{n}} \centerdot{x}^{−\mathrm{2}} +\frac{\mathrm{1}}{\left(\mathrm{1}\right)^{{n}} \centerdot{x}^{−\mathrm{2}} }\right)^{\mathrm{2}} +\left(\left(\mathrm{1}\right)^{{n}} \centerdot{x}^{−\mathrm{2}} +\frac{\mathrm{1}}{\left(\mathrm{1}\right)^{{n}} \centerdot{x}^{−\mathrm{2}} }\right)^{\mathrm{2}} +\left(\left(\mathrm{1}\right)^{{n}} +\frac{\mathrm{1}}{\left(\mathrm{1}\right)^{{n}} }\right)^{\mathrm{2}} \right\} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left({x}^{−\mathrm{2}} +\frac{\mathrm{1}}{{x}^{−\mathrm{2}} }\right)^{\mathrm{2}} +\left({x}^{−\mathrm{1}} +\frac{\mathrm{1}}{{x}^{−\mathrm{1}} }\right)^{\mathrm{2}} +\left(\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}\right)^{\mathrm{2}} \right\}\right. \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left(\left(\mathrm{2}\right)^{\mathrm{2}} \right\}\right. \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left(\frac{{x}^{\mathrm{3}} \centerdot{x}+\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{4}\right\} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left(\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\frac{−{x}}{{x}}\right)^{\mathrm{2}} +\mathrm{4}\right\} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left(\frac{−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\frac{−{x}}{{x}}\right)^{\mathrm{2}} +\mathrm{4}\right\} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left\{\left(−\mathrm{1}\right)^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\right\} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left(\mathrm{6}\right)=\mathrm{6}×\mathrm{9}=\mathrm{54} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *