Question Number 183107 by mr W last updated on 21/Dec/22
Commented by mr W last updated on 20/Dec/22

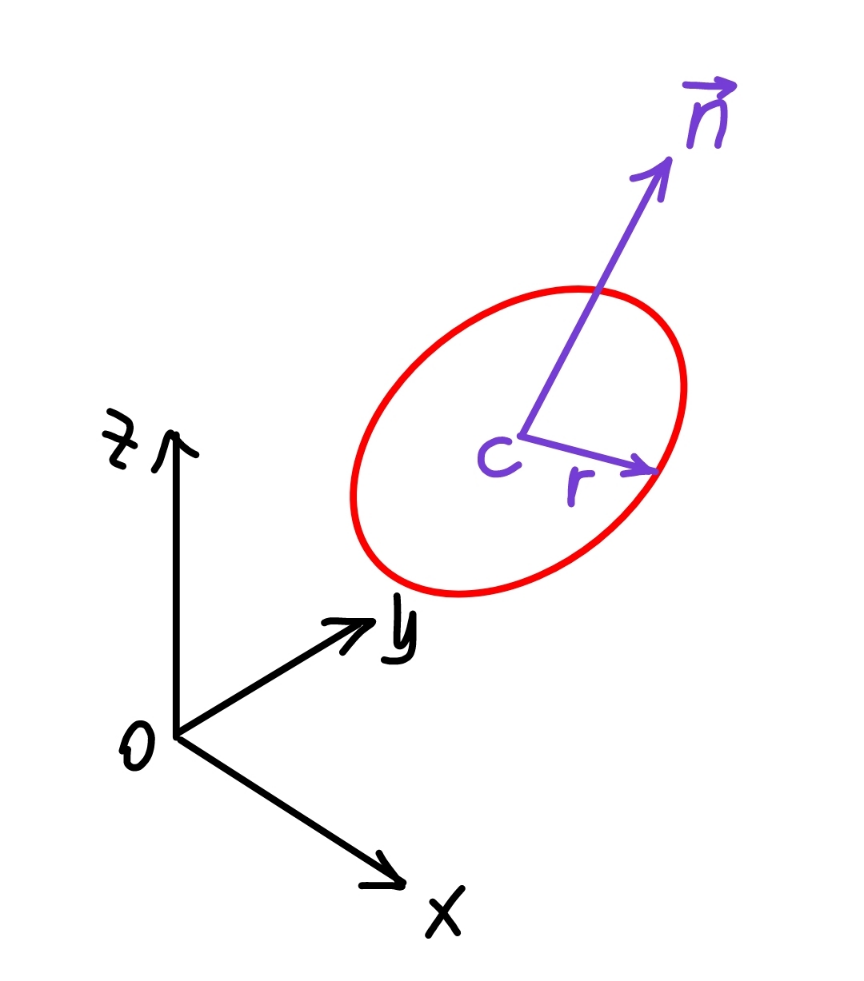
$${find}\:{the}\:{equation}\:{of}\:{the}\:{circle}\:{with} \\ $$$${radius}\:{r}\:{and}\:{center}\:{at}\:{C}\left({a},{b},{c}\right).\:{the} \\ $$$${normal}\:{of}\:{the}\:{plane}\:{in}\:{which}\:{the} \\ $$$${circle}\:{lies}\:{is}\:\overset{\rightarrow} {{n}}=\left(\alpha,\beta,\gamma\right). \\ $$
Answered by mr W last updated on 21/Dec/22

Commented by mr W last updated on 21/Dec/22
![the eqn. of the plane containing the circle is α(x−a)+β(y−b)+γ(z−c)=0 with z=c: α(x−a)+β(y−b)+γ(c−c)=0 αx+βy=αa+βb u^→ =(−β,α,0) u_1 ^→ =(−(β/( (√(α^2 +β^2 )))),(α/( (√(α^2 +β^2 )))),0) v^→ =n^→ ×u^→ = [(α,β,γ),((−β),α,0) ]=(−αγ,βγ,α^2 +β^2 ) v_1 ^→ =(−((αγ)/( (√((α^2 +β^2 )(α^2 +β^2 +γ^2 ))))),((βγ)/( (√((α^2 +β^2 )(α^2 +β^2 +γ^2 ))))),((√(α^2 +β^2 ))/( (√(α^2 +β^2 +γ^2 ))))) eqn. of circle with parameter θ: P(x,y,z)=(a,b,c)+r cos θ u_1 ^→ +r sin θ v_1 ^→ x=a−((βr cos θ)/( (√(α^2 +β^2 ))))−((αγr sin θ)/( (√((α^2 +β^2 )(α^2 +β^2 +γ^2 ))))) y=b+((αr cos θ)/( (√(α^2 +β^2 ))))+((βγr sin θ)/( (√((α^2 +β^2 )(α^2 +β^2 +γ^2 ))))) z=c+(((√(α^2 +β^2 )) r sin θ)/( (√(α^2 +β^2 +γ^2 ))))](https://www.tinkutara.com/question/Q183129.png)
$${the}\:{eqn}.\:{of}\:{the}\:{plane}\:{containing}\:{the} \\ $$$${circle}\:{is} \\ $$$$\alpha\left({x}−{a}\right)+\beta\left({y}−{b}\right)+\gamma\left({z}−{c}\right)=\mathrm{0} \\ $$$${with}\:{z}={c}: \\ $$$$\alpha\left({x}−{a}\right)+\beta\left({y}−{b}\right)+\gamma\left({c}−{c}\right)=\mathrm{0} \\ $$$$\alpha{x}+\beta{y}=\alpha{a}+\beta{b} \\ $$$$\overset{\rightarrow} {{u}}=\left(−\beta,\alpha,\mathrm{0}\right) \\ $$$$\overset{\rightarrow} {{u}}_{\mathrm{1}} =\left(−\frac{\beta}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }},\frac{\alpha}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }},\mathrm{0}\right) \\ $$$$\overset{\rightarrow} {{v}}=\overset{\rightarrow} {{n}}×\overset{\rightarrow} {{u}}=\begin{bmatrix}{\alpha}&{\beta}&{\gamma}\\{−\beta}&{\alpha}&{\mathrm{0}}\end{bmatrix}=\left(−\alpha\gamma,\beta\gamma,\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right) \\ $$$$\overset{\rightarrow} {{v}}_{\mathrm{1}} =\left(−\frac{\alpha\gamma}{\:\sqrt{\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)}},\frac{\beta\gamma}{\:\sqrt{\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)}},\frac{\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }}\right) \\ $$$${eqn}.\:{of}\:{circle}\:{with}\:{parameter}\:\theta: \\ $$$${P}\left({x},{y},{z}\right)=\left({a},{b},{c}\right)+{r}\:\mathrm{cos}\:\theta\:\overset{\rightarrow} {{u}}_{\mathrm{1}} +{r}\:\mathrm{sin}\:\theta\:\overset{\rightarrow} {{v}}_{\mathrm{1}} \\ $$$${x}={a}−\frac{\beta{r}\:\mathrm{cos}\:\theta}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}−\frac{\alpha\gamma{r}\:\mathrm{sin}\:\theta}{\:\sqrt{\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)}} \\ $$$${y}={b}+\frac{\alpha{r}\:\mathrm{cos}\:\theta}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}+\frac{\beta\gamma{r}\:\mathrm{sin}\:\theta}{\:\sqrt{\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)}} \\ $$$${z}={c}+\frac{\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }\:{r}\:\mathrm{sin}\:\theta}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }} \\ $$
