Question Number 183185 by mnjuly1970 last updated on 22/Dec/22
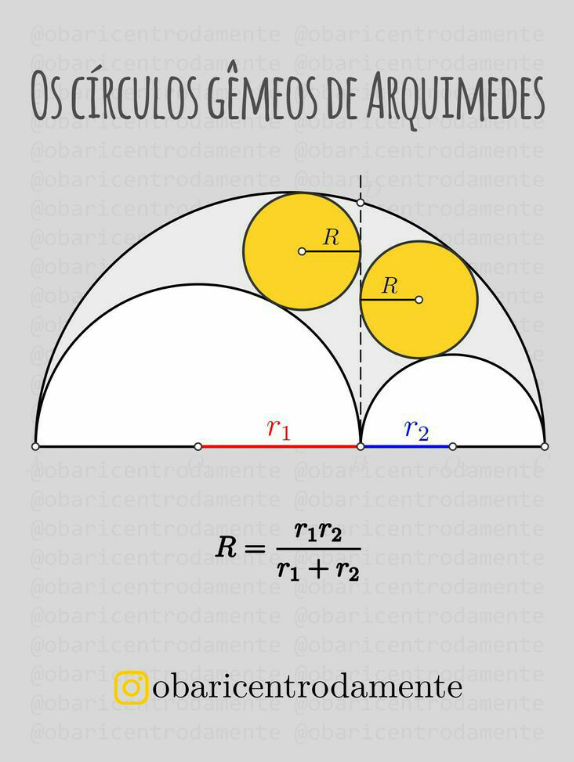
Answered by mr W last updated on 23/Dec/22
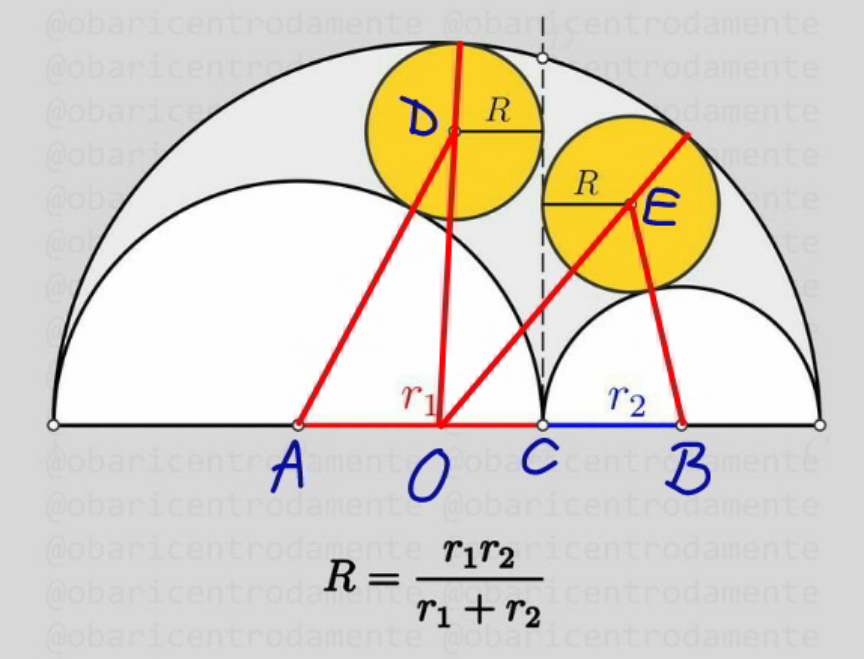
Commented by mr W last updated on 23/Dec/22
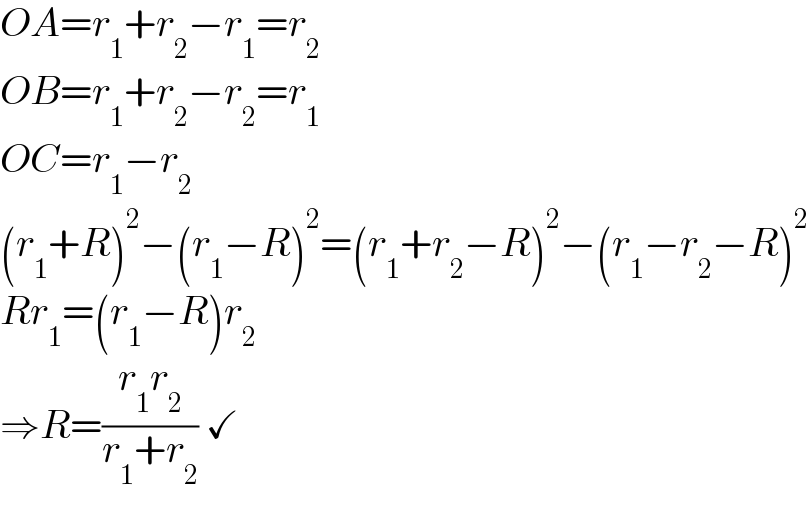
$${OA}={r}_{\mathrm{1}} +{r}_{\mathrm{2}} −{r}_{\mathrm{1}} ={r}_{\mathrm{2}} \\ $$$${OB}={r}_{\mathrm{1}} +{r}_{\mathrm{2}} −{r}_{\mathrm{2}} ={r}_{\mathrm{1}} \\ $$$${OC}={r}_{\mathrm{1}} −{r}_{\mathrm{2}} \\ $$$$\left({r}_{\mathrm{1}} +{R}\right)^{\mathrm{2}} −\left({r}_{\mathrm{1}} −{R}\right)^{\mathrm{2}} =\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} −{R}\right)^{\mathrm{2}} −\left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} −{R}\right)^{\mathrm{2}} \\ $$$${Rr}_{\mathrm{1}} =\left({r}_{\mathrm{1}} −{R}\right){r}_{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{{r}_{\mathrm{1}} {r}_{\mathrm{2}} }{{r}_{\mathrm{1}} +{r}_{\mathrm{2}} }\:\checkmark \\ $$
