Question Number 183216 by mr W last updated on 23/Dec/22
Commented by mr W last updated on 23/Dec/22
Commented by mr W last updated on 23/Dec/22
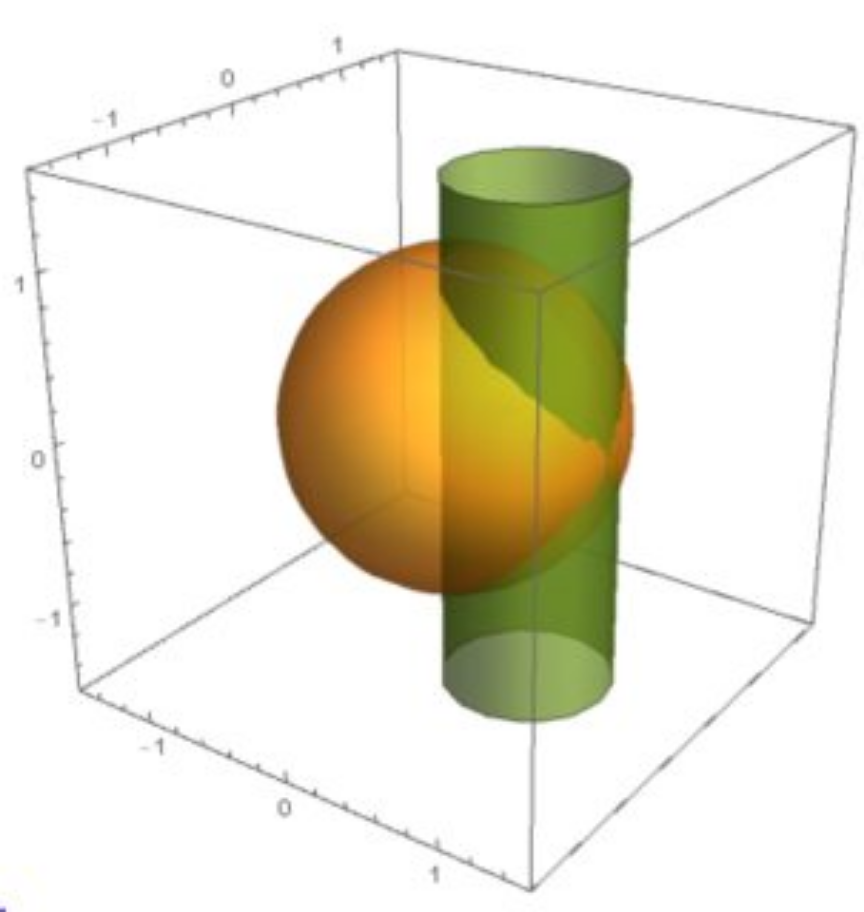
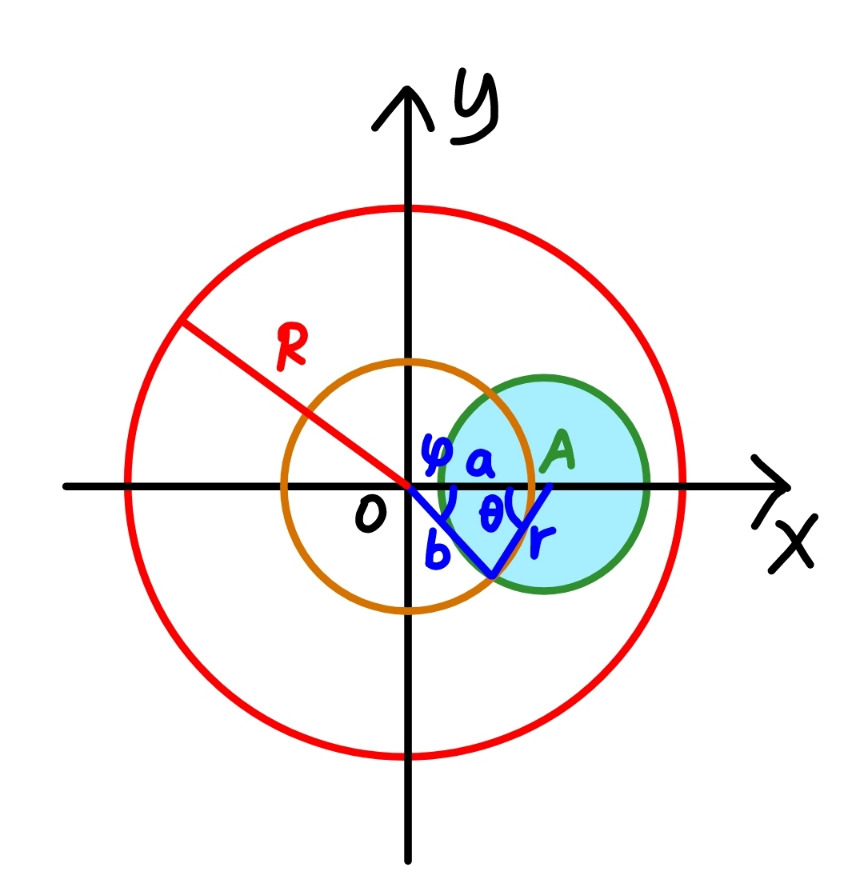
$${the}\:{general}\:{case}\:{for}\:{sphere}\:\left({red}\right)\:{cut} \\ $$$${by}\:{a}\:{cylinder}\:\left({green}\right) \\ $$
Answered by mr W last updated on 23/Dec/22

$${given}:\:{R},\:{r},\:{a} \\ $$$${find}\:{the}\:{volume}\:{of}\:{the}\:{portion}\:{of} \\ $$$${the}\:{sphere}\:{cut}\:{by}\:{the}\:{cylinder} \\ $$$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{ar}\:\mathrm{cos}\:\theta \\ $$$${z}=\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} −{r}^{\mathrm{2}} +\mathrm{2}{ar}\:\mathrm{cos}\:\theta} \\ $$$${a}\:\mathrm{sin}\:\theta=\left({a}−{r}\:\mathrm{cos}\:\theta\right)\:\mathrm{tan}\:\varphi \\ $$$$\Rightarrow\varphi=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}\:\mathrm{sin}\:\theta}{{a}−{r}\:\mathrm{cos}\:\theta}\right) \\ $$$$\mathrm{2}{bdb}=\mathrm{2}{ar}\:\mathrm{sin}\:\theta\:{d}\theta \\ $$$${dS}=\mathrm{2}\varphi{bdb}=\mathrm{2}{ar}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}\:\mathrm{sin}\:\theta}{{a}−{r}\:\mathrm{cos}\:\theta}\right)\:\mathrm{sin}\:\theta\:{d}\theta \\ $$$${V}=\mathrm{2}\int_{\mathrm{0}} ^{\pi} {zdS} \\ $$$${V}=\mathrm{4}{arR}\int_{\mathrm{0}} ^{\pi} \sqrt{\mathrm{1}−\left(\frac{{a}}{{R}}\right)^{\mathrm{2}} −\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} +\frac{\mathrm{2}{ar}}{{R}^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\theta}{\mathrm{1}−\frac{{r}}{{a}}\:\mathrm{cos}\:\theta}\right)\:\mathrm{sin}\:\theta\:{d}\theta \\ $$$${let}\:\lambda=\frac{{a}}{{R}},\:\mu=\frac{{r}}{{R}} \\ $$$$\Rightarrow{V}=\mathrm{4}\mu\lambda{R}^{\mathrm{3}} \int_{\mathrm{0}} ^{\pi} \sqrt{\mathrm{1}−\mu^{\mathrm{2}} −\lambda^{\mathrm{2}} +\mathrm{2}\mu\lambda\:\mathrm{cos}\:\theta}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\theta}{\mathrm{1}−\frac{\mu}{\lambda}\:\mathrm{cos}\:\theta}\right)\:\mathrm{sin}\:\theta\:{d}\theta \\ $$
Commented by manxsol last updated on 23/Dec/22
$${Thanks},\:{Sir}\:{W},{applause} \\ $$$$\:{for}\:{your}\:{effort},\:{very}\:{clear} \\ $$$$ \\ $$
Commented by mr W last updated on 23/Dec/22

$${thank}\:{you}\:{too}! \\ $$
