Question Number 183254 by HeferH last updated on 24/Dec/22

Answered by TUN last updated on 24/Dec/22
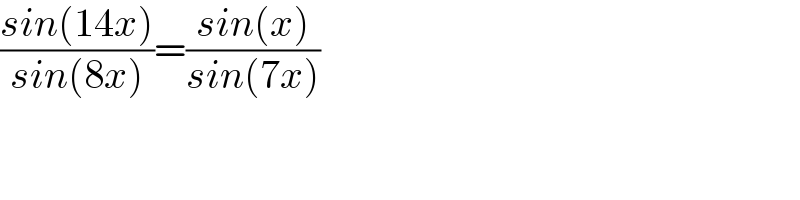
$$\frac{{sin}\left(\mathrm{14}{x}\right)}{{sin}\left(\mathrm{8}{x}\right)}=\frac{{sin}\left({x}\right)}{{sin}\left(\mathrm{7}{x}\right)} \\ $$
Answered by a.lgnaoui last updated on 25/Dec/22
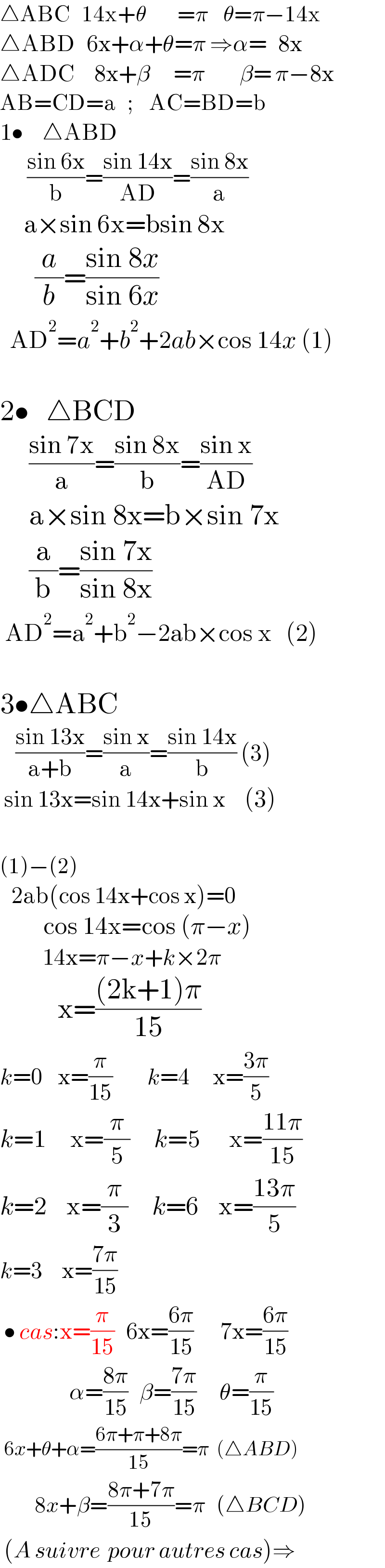
$$\bigtriangleup\mathrm{ABC}\:\:\:\mathrm{14x}+\theta\:\:\:\:\:\:\:\:=\pi\:\:\:\:\theta=\pi−\mathrm{14x} \\ $$$$\bigtriangleup\mathrm{ABD}\:\:\:\mathrm{6x}+\alpha+\theta=\pi\:\Rightarrow\alpha=\:\:\:\mathrm{8x} \\ $$$$\bigtriangleup\mathrm{ADC}\:\:\:\:\:\mathrm{8x}+\beta\:\:\:\:\:\:=\pi\:\:\:\:\:\:\:\:\:\beta=\:\pi−\mathrm{8x} \\ $$$$\mathrm{AB}=\mathrm{CD}=\mathrm{a}\:\:\:;\:\:\:\:\mathrm{AC}=\mathrm{BD}=\mathrm{b} \\ $$$$\mathrm{1}\bullet\:\:\:\:\:\bigtriangleup\mathrm{ABD} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{6x}}{\mathrm{b}}=\frac{\mathrm{sin}\:\mathrm{14x}}{\mathrm{AD}}=\frac{\mathrm{sin}\:\mathrm{8x}}{\mathrm{a}} \\ $$$$\:\:\:\:\:\mathrm{a}×\mathrm{sin}\:\mathrm{6x}=\mathrm{bsin}\:\mathrm{8x} \\ $$$$\:\:\:\:\:\:\frac{{a}}{{b}}=\frac{\mathrm{sin}\:\mathrm{8}{x}}{\mathrm{sin}\:\mathrm{6}{x}} \\ $$$$\:\:\mathrm{AD}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}×\mathrm{cos}\:\mathrm{14}{x}\:\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\: \\ $$$$\mathrm{2}\bullet\:\:\:\bigtriangleup\mathrm{BCD} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{7x}}{\mathrm{a}}=\frac{\mathrm{sin}\:\mathrm{8x}}{\mathrm{b}}=\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{AD}} \\ $$$$\:\:\:\:\:\mathrm{a}×\mathrm{sin}\:\mathrm{8x}=\mathrm{b}×\mathrm{sin}\:\mathrm{7x} \\ $$$$\:\:\:\:\:\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{sin}\:\mathrm{7x}}{\mathrm{sin}\:\mathrm{8x}}\:\:\:\: \\ $$$$\:\mathrm{AD}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}×\mathrm{cos}\:\mathrm{x}\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{3}\bullet\bigtriangleup\mathrm{ABC} \\ $$$$\:\:\:\:\frac{\mathrm{sin}\:\mathrm{13x}}{\mathrm{a}+\mathrm{b}}=\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{a}}=\frac{\mathrm{sin}\:\mathrm{14x}}{\mathrm{b}}\:\left(\mathrm{3}\right) \\ $$$$\:\mathrm{sin}\:\mathrm{13x}=\mathrm{sin}\:\mathrm{14x}+\mathrm{sin}\:\mathrm{x}\:\:\:\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\:\: \\ $$$$\:\:\:\mathrm{2ab}\left(\mathrm{cos}\:\mathrm{14x}+\mathrm{cos}\:\mathrm{x}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{14x}=\mathrm{cos}\:\left(\pi−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{14x}=\pi−{x}+{k}×\mathrm{2}\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{15}} \\ $$$${k}=\mathrm{0}\:\:\:\:\mathrm{x}=\frac{\pi}{\mathrm{15}}\:\:\:\:\:\:\:\:\:{k}=\mathrm{4}\:\:\:\:\:\:\mathrm{x}=\frac{\mathrm{3}\pi}{\mathrm{5}} \\ $$$${k}=\mathrm{1}\:\:\:\:\:\mathrm{x}=\frac{\pi}{\mathrm{5}}\:\:\:\:\:{k}=\mathrm{5}\:\:\:\:\:\:\mathrm{x}=\frac{\mathrm{11}\pi}{\mathrm{15}} \\ $$$${k}=\mathrm{2}\:\:\:\:\mathrm{x}=\frac{\pi}{\mathrm{3}}\:\:\:\:\:{k}=\mathrm{6}\:\:\:\:\mathrm{x}=\frac{\mathrm{13}\pi}{\mathrm{5}} \\ $$$${k}=\mathrm{3}\:\:\:\:\:\mathrm{x}=\frac{\mathrm{7}\pi}{\mathrm{15}}\:\:\:\:\:\:\:\: \\ $$$$\:\bullet\:{cas}:\mathrm{x}=\frac{\pi}{\mathrm{15}}\:\:\:\mathrm{6x}=\frac{\mathrm{6}\pi}{\mathrm{15}}\:\:\:\:\:\:\:\mathrm{7x}=\frac{\mathrm{6}\pi}{\mathrm{15}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\alpha=\frac{\mathrm{8}\pi}{\mathrm{15}}\:\:\:\beta=\frac{\mathrm{7}\pi}{\mathrm{15}}\:\:\:\:\:\:\theta=\frac{\pi}{\mathrm{15}} \\ $$$$\:\mathrm{6}{x}+\theta+\alpha=\frac{\mathrm{6}\pi+\pi+\mathrm{8}\pi}{\mathrm{15}}=\pi\:\:\left(\bigtriangleup{ABD}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{8}{x}+\beta=\frac{\mathrm{8}\pi+\mathrm{7}\pi}{\mathrm{15}}=\pi\:\:\:\left(\bigtriangleup{BCD}\right) \\ $$$$\:\left({A}\:{suivre}\:\:{pour}\:{autres}\:{cas}\right)\Rightarrow \\ $$
Commented by a.lgnaoui last updated on 25/Dec/22

