Question Number 18327 by mondodotto@gmail.com last updated on 18/Jul/17
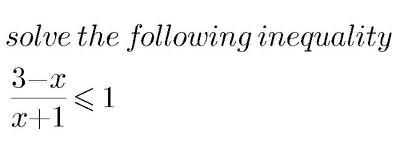
Commented by mondodotto@gmail.com last updated on 18/Jul/17

$$\mathrm{please}\:\mathrm{help}!! \\ $$
Answered by ajfour last updated on 19/Jul/17
$$\mathrm{if}\:\mathrm{x}+\mathrm{1}>\mathrm{0}\:\Rightarrow\:\mathrm{x}>−\mathrm{1} \\ $$$$\mathrm{3}−\mathrm{x}\leqslant\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{2x}\geqslant\mathrm{2} \\ $$$$\mathrm{x}\geqslant\mathrm{1}\:\: \\ $$$$\mathrm{if}\:\mathrm{x}+\mathrm{1}<\mathrm{0}\:\:\:\Rightarrow\:\:\mathrm{x}<−\mathrm{1} \\ $$$$\mathrm{3}−\mathrm{x}\geqslant\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{2x}\leqslant\mathrm{2} \\ $$$$\mathrm{x}\leqslant\mathrm{1}\:\:\mathrm{so}\:\:\:\mathrm{x}<−\mathrm{1} \\ $$$$\mathrm{combining}\:\mathrm{the}\:\mathrm{result}\:\mathrm{of}\:\mathrm{the}\:\mathrm{two} \\ $$$$\mathrm{cases}:\:\:\:\:\:\:\mathrm{x}\in\left(−\infty,−\mathrm{1}\right)\cup\left[\mathrm{1},\infty\right) \\ $$
