Question Number 183295 by ajfour last updated on 24/Dec/22
Commented by ajfour last updated on 24/Dec/22
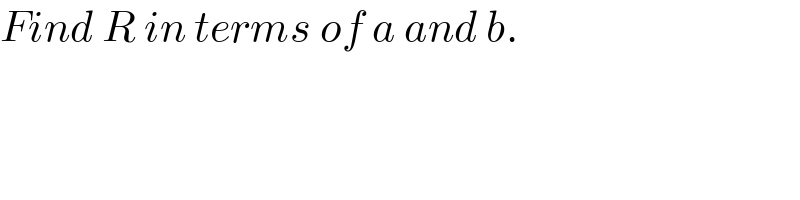
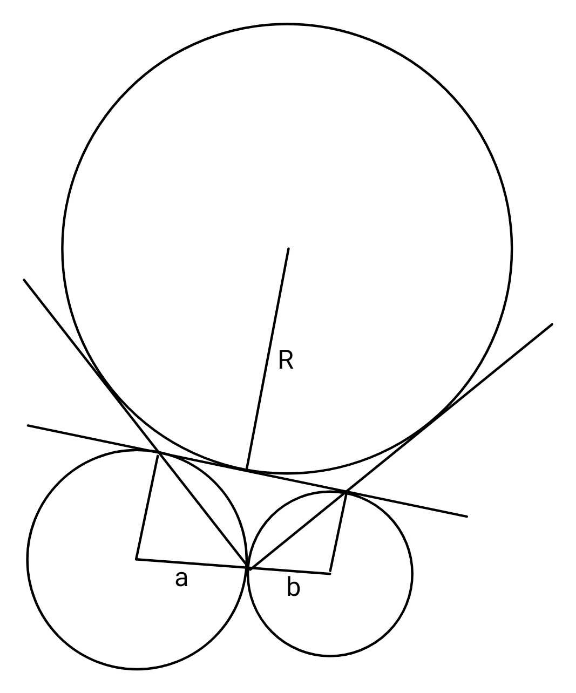
$${Find}\:{R}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}. \\ $$
Answered by ajfour last updated on 24/Dec/22
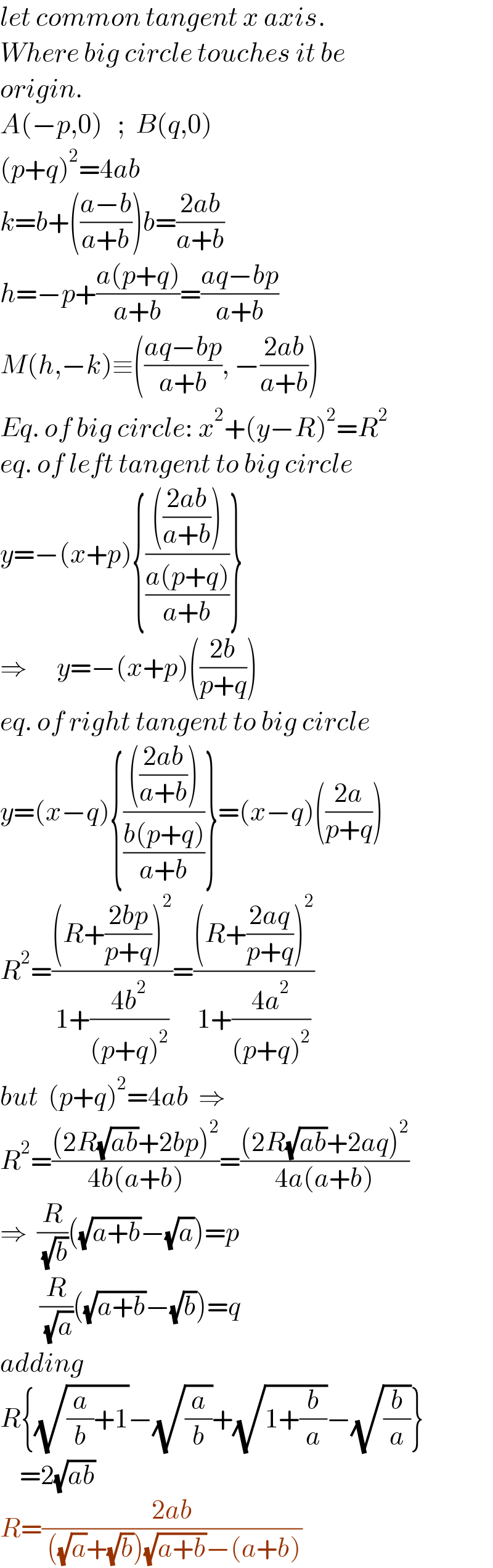
$${let}\:{common}\:{tangent}\:{x}\:{axis}. \\ $$$${Where}\:{big}\:{circle}\:{touches}\:{it}\:{be} \\ $$$${origin}. \\ $$$${A}\left(−{p},\mathrm{0}\right)\:\:\:;\:\:{B}\left({q},\mathrm{0}\right) \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} =\mathrm{4}{ab} \\ $$$${k}={b}+\left(\frac{{a}−{b}}{{a}+{b}}\right){b}=\frac{\mathrm{2}{ab}}{{a}+{b}} \\ $$$${h}=−{p}+\frac{{a}\left({p}+{q}\right)}{{a}+{b}}=\frac{{aq}−{bp}}{{a}+{b}} \\ $$$${M}\left({h},−{k}\right)\equiv\left(\frac{{aq}−{bp}}{{a}+{b}},\:−\frac{\mathrm{2}{ab}}{{a}+{b}}\right) \\ $$$${Eq}.\:{of}\:{big}\:{circle}:\:{x}^{\mathrm{2}} +\left({y}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${eq}.\:{of}\:{left}\:{tangent}\:{to}\:{big}\:{circle} \\ $$$${y}=−\left({x}+{p}\right)\left\{\frac{\left(\frac{\mathrm{2}{ab}}{{a}+{b}}\right)}{\frac{{a}\left({p}+{q}\right)}{{a}+{b}}}\right\} \\ $$$$\Rightarrow\:\:\:\:\:\:{y}=−\left({x}+{p}\right)\left(\frac{\mathrm{2}{b}}{{p}+{q}}\right) \\ $$$${eq}.\:{of}\:{right}\:{tangent}\:{to}\:{big}\:{circle} \\ $$$${y}=\left({x}−{q}\right)\left\{\frac{\left(\frac{\mathrm{2}{ab}}{{a}+{b}}\right)}{\frac{{b}\left({p}+{q}\right)}{{a}+{b}}}\right\}=\left({x}−{q}\right)\left(\frac{\mathrm{2}{a}}{{p}+{q}}\right) \\ $$$${R}^{\mathrm{2}} =\frac{\left({R}+\frac{\mathrm{2}{bp}}{{p}+{q}}\right)^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{4}{b}^{\mathrm{2}} }{\left({p}+{q}\right)^{\mathrm{2}} }}=\frac{\left({R}+\frac{\mathrm{2}{aq}}{{p}+{q}}\right)^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{4}{a}^{\mathrm{2}} }{\left({p}+{q}\right)^{\mathrm{2}} }} \\ $$$${but}\:\:\left({p}+{q}\right)^{\mathrm{2}} =\mathrm{4}{ab}\:\:\Rightarrow \\ $$$${R}^{\mathrm{2}} =\frac{\left(\mathrm{2}{R}\sqrt{{ab}}+\mathrm{2}{bp}\right)^{\mathrm{2}} }{\mathrm{4}{b}\left({a}+{b}\right)}=\frac{\left(\mathrm{2}{R}\sqrt{{ab}}+\mathrm{2}{aq}\right)^{\mathrm{2}} }{\mathrm{4}{a}\left({a}+{b}\right)} \\ $$$$\Rightarrow\:\:\frac{{R}}{\:\sqrt{{b}}}\left(\sqrt{{a}+{b}}−\sqrt{{a}}\right)={p} \\ $$$$\:\:\:\:\:\:\:\:\frac{{R}}{\:\sqrt{{a}}}\left(\sqrt{{a}+{b}}−\sqrt{{b}}\right)={q} \\ $$$${adding} \\ $$$${R}\left\{\sqrt{\frac{{a}}{{b}}+\mathrm{1}}−\sqrt{\frac{{a}}{{b}}}+\sqrt{\mathrm{1}+\frac{{b}}{{a}}}−\sqrt{\frac{{b}}{{a}}}\right\} \\ $$$$\:\:\:\:=\mathrm{2}\sqrt{{ab}} \\ $$$${R}=\frac{\mathrm{2}{ab}}{\:\left(\sqrt{{a}}+\sqrt{{b}}\right)\sqrt{{a}+{b}}−\left({a}+{b}\right)} \\ $$
Commented by mr W last updated on 24/Dec/22
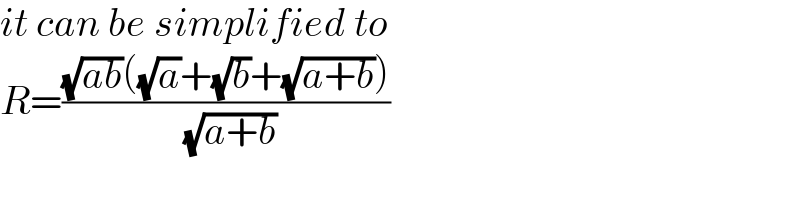
$${it}\:{can}\:{be}\:{simplified}\:{to} \\ $$$${R}=\frac{\sqrt{{ab}}\left(\sqrt{{a}}+\sqrt{{b}}+\sqrt{{a}+{b}}\right)}{\:\sqrt{{a}+{b}}} \\ $$
Answered by mr W last updated on 24/Dec/22
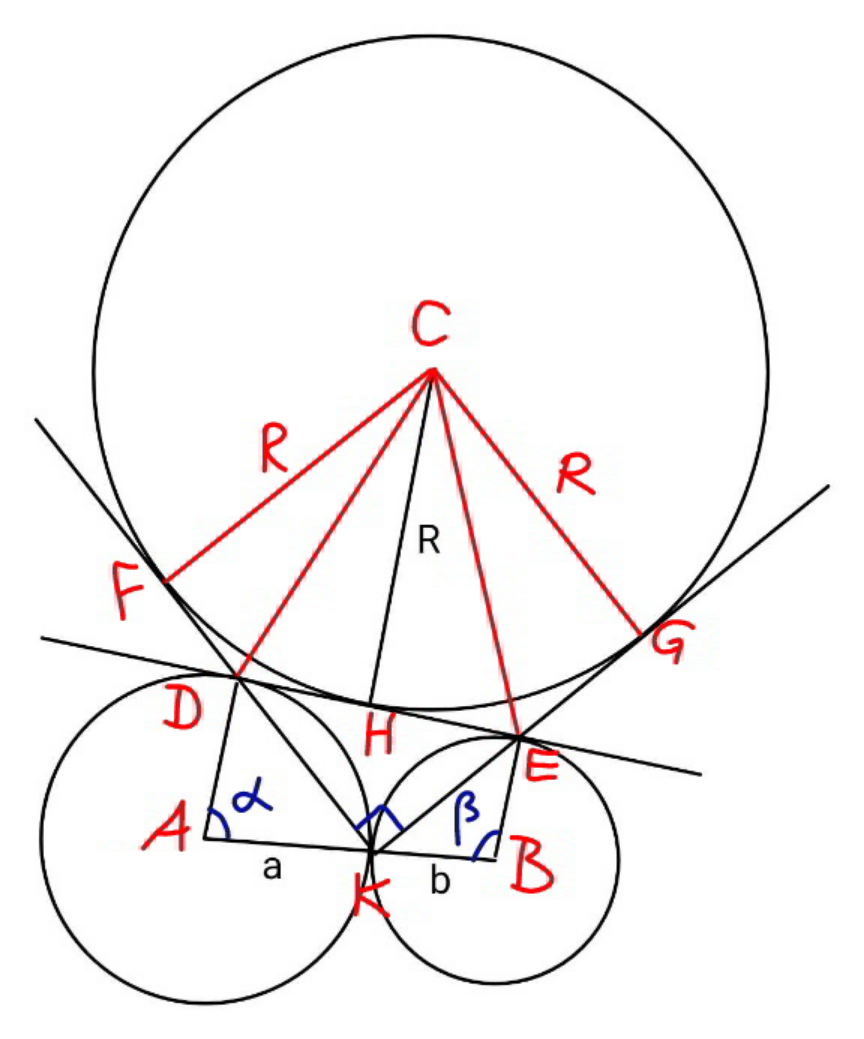
Commented by mr W last updated on 24/Dec/22

$$\mathrm{cos}\:\alpha=\frac{{a}−{b}}{{a}+{b}} \\ $$$${KF}={KG}={R} \\ $$$${KD}={a}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)}=\frac{\mathrm{2}{a}\sqrt{{b}}}{\:\sqrt{{a}+{b}}} \\ $$$${similarly}\:{KE}=\frac{\mathrm{2}{b}\sqrt{{a}}}{\:\sqrt{{a}+{b}}} \\ $$$${DE}={FD}+{GE}=\mathrm{2}{R}−{DK}−{EK}=\mathrm{2}{R}−\frac{\mathrm{2}\sqrt{{ab}}\left(\sqrt{{a}}+\sqrt{{b}}\right)}{\:\sqrt{{a}+{b}}} \\ $$$${DE}=\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{ab}} \\ $$$$\mathrm{2}{R}−\frac{\mathrm{2}\sqrt{{ab}}\left(\sqrt{{a}}+\sqrt{{b}}\right)}{\:\sqrt{{a}+{b}}}=\mathrm{2}\sqrt{{ab}} \\ $$$$\Rightarrow{R}=\frac{\sqrt{{ab}}\left(\sqrt{{a}+{b}}+\sqrt{{a}}+\sqrt{{b}}\right)}{\:\sqrt{{a}+{b}}} \\ $$
Commented by ajfour last updated on 24/Dec/22

$${Thanks}\:{Sir}.\:{Excellent}\:{way}! \\ $$
