Question-183307

Facebook Tweet Pin

Question Number 183307 by ajfour last updated on 24/Dec/22

Commented by ajfour last updated on 24/Dec/22

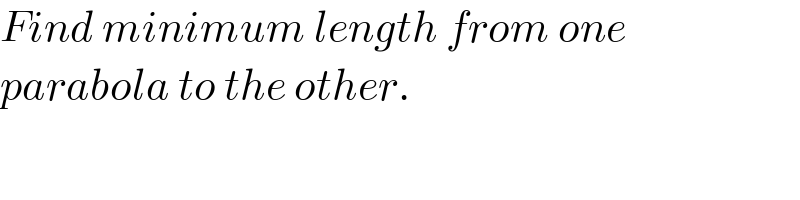
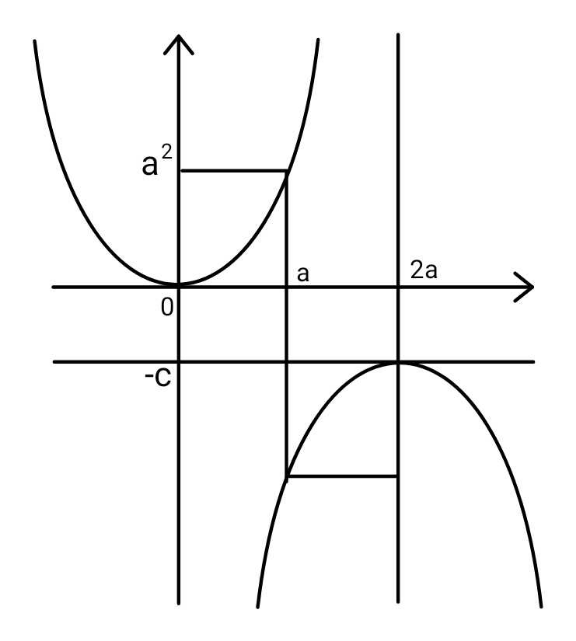
$${Find}\:{minimum}\:{length}\:{from}\:{one} \\ $$$${parabola}\:{to}\:{the}\:{other}. \\ $$

Answered by mr W last updated on 24/Dec/22

Commented by mr W last updated on 25/Dec/22

P(p,p^2 ) M(a,−(c/2)) ⇒c≥−2a^2 tan θ=2p=((a−p)/(p^2 +(c/2))) p^3 +(((c+1)/2))p−(a/2)=0 if (a^2 /(16))+(((c+1)^3 )/(216))≥0, i.e. c≥−1−3((a^2 /2))^(1/3) : p=(((√((a^2 /(16))+(((c+1)^3 )/(216))))+(a/4)))^(1/3) −(((√((a^2 /(16))+(((c+1)^3 )/(216))))−(a/4)))^(1/3) if (a^2 /(16))+(((c+1)^3 )/(216))<0, i.e. −2a^2 ≤c<−1−3((a^2 /2))^(1/3) : p=2(√(−((c+1)/6))) sin {(π/3)−(1/3) sin^(−1) ((3a)/(2(c+1)))(√(−(6/(c+1))))} d_(min) =2×PM=2(√((a−p)^2 +(p^2 +(c/2))^2 ))

$${P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${M}\left({a},−\frac{{c}}{\mathrm{2}}\right)\:\Rightarrow{c}\geqslant−\mathrm{2}{a}^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p}=\frac{{a}−{p}}{{p}^{\mathrm{2}} +\frac{{c}}{\mathrm{2}}} \\ $$$${p}^{\mathrm{3}} +\left(\frac{{c}+\mathrm{1}}{\mathrm{2}}\right){p}−\frac{{a}}{\mathrm{2}}=\mathrm{0} \\ $$$${if}\:\frac{{a}^{\mathrm{2}} }{\mathrm{16}}+\frac{\left({c}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{216}}\geqslant\mathrm{0},\:{i}.{e}.\:{c}\geqslant−\mathrm{1}−\mathrm{3}\sqrt[{\mathrm{3}}]{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}}: \\ $$$${p}=\sqrt[{\mathrm{3}}]{\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{16}}+\frac{\left({c}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{216}}}+\frac{{a}}{\mathrm{4}}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{16}}+\frac{\left({c}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{216}}}−\frac{{a}}{\mathrm{4}}} \\ $$$${if}\:\frac{{a}^{\mathrm{2}} }{\mathrm{16}}+\frac{\left({c}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{216}}<\mathrm{0},\:{i}.{e}.\:−\mathrm{2}{a}^{\mathrm{2}} \leqslant{c}<−\mathrm{1}−\mathrm{3}\sqrt[{\mathrm{3}}]{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}}: \\ $$$${p}=\mathrm{2}\sqrt{−\frac{{c}+\mathrm{1}}{\mathrm{6}}}\:\mathrm{sin}\:\left\{\frac{\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}{a}}{\mathrm{2}\left({c}+\mathrm{1}\right)}\sqrt{−\frac{\mathrm{6}}{{c}+\mathrm{1}}}\right\} \\ $$$${d}_{{min}} =\mathrm{2}×{PM}=\mathrm{2}\sqrt{\left({a}−{p}\right)^{\mathrm{2}} +\left({p}^{\mathrm{2}} +\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$

Commented by mr W last updated on 24/Dec/22