Question-183376

Question Number 183376 by TUN last updated on 25/Dec/22

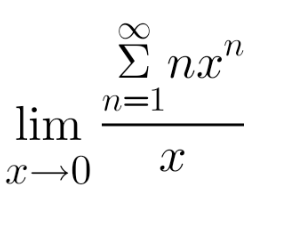
Commented by CElcedricjunior last updated on 25/Dec/22

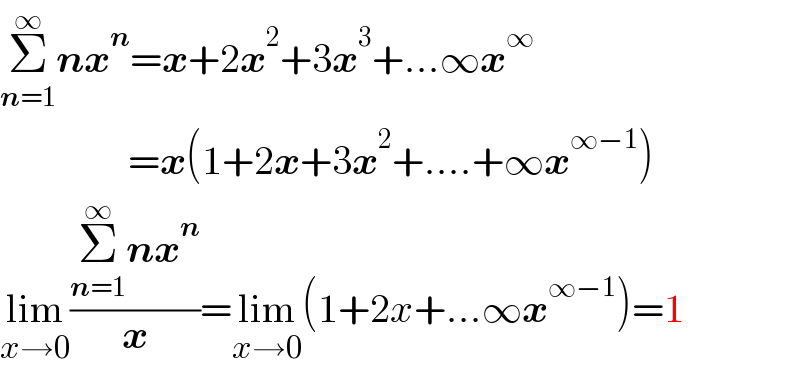
Σ_(n=1) ^∞ nx^n =x+2x^2 +3x^3 +...∞x^∞ =x(1+2x+3x^2 +....+∞x^(∞−1) ) lim_(x→0) ((Σ_(n=1) ^∞ nx^n )/x)=lim_(x→0) (1+2x+...∞x^(∞−1) )=1

$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{{nx}}^{\boldsymbol{{n}}} =\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{{x}}^{\mathrm{3}} +…\infty\boldsymbol{{x}}^{\infty} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{{x}}\left(\mathrm{1}+\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\boldsymbol{{x}}^{\mathrm{2}} +….+\infty\boldsymbol{{x}}^{\infty−\mathrm{1}} \right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{{nx}}^{\boldsymbol{{n}}} }{\boldsymbol{{x}}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{2}{x}+…\infty\boldsymbol{{x}}^{\infty−\mathrm{1}} \right)=\mathrm{1} \\ $$

Answered by TheSupreme last updated on 25/Dec/22

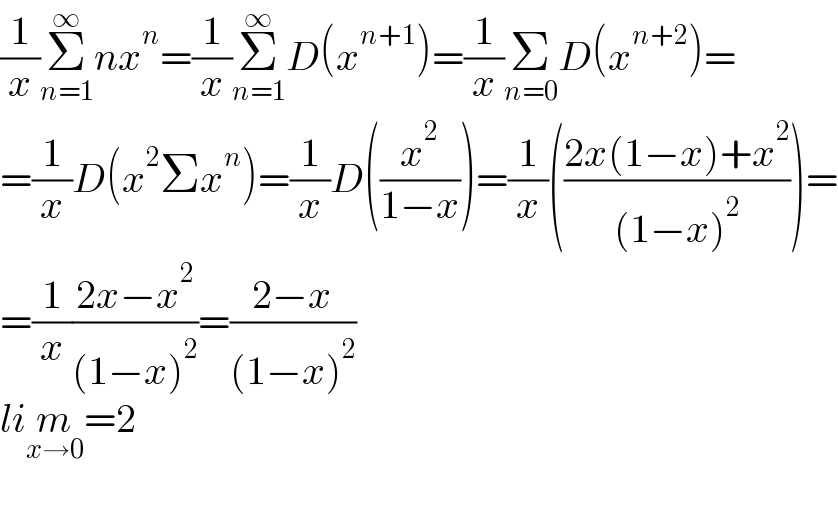
(1/x)Σ_(n=1) ^∞ nx^n =(1/x)Σ_(n=1) ^∞ D(x^(n+1) )=(1/x)Σ_(n=0) D(x^(n+2) )= =(1/x)D(x^2 Σx^n )=(1/x)D((x^2 /(1−x)))=(1/x)(((2x(1−x)+x^2 )/((1−x)^2 )))= =(1/x)((2x−x^2 )/((1−x)^2 ))=((2−x)/((1−x)^2 )) lim_(x→0) =2

$$\frac{\mathrm{1}}{{x}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}} =\frac{\mathrm{1}}{{x}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{D}\left({x}^{{n}+\mathrm{1}} \right)=\frac{\mathrm{1}}{{x}}\underset{{n}=\mathrm{0}} {\sum}{D}\left({x}^{{n}+\mathrm{2}} \right)= \\ $$$$=\frac{\mathrm{1}}{{x}}{D}\left({x}^{\mathrm{2}} \Sigma{x}^{{n}} \right)=\frac{\mathrm{1}}{{x}}{D}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}}\right)=\frac{\mathrm{1}}{{x}}\left(\frac{\mathrm{2}{x}\left(\mathrm{1}−{x}\right)+{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\right)= \\ $$$$=\frac{\mathrm{1}}{{x}}\frac{\mathrm{2}{x}−{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\frac{\mathrm{2}−{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}=\mathrm{2} \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 25/Dec/22

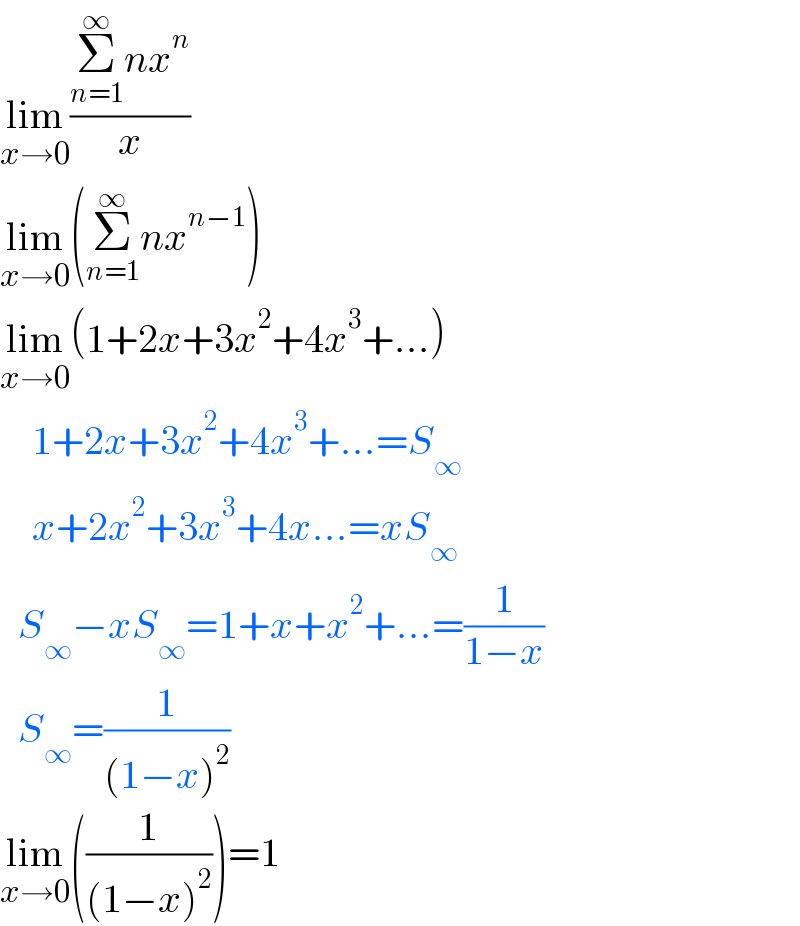
lim_(x→0) ((Σ_(n=1) ^∞ nx^n )/x) lim_(x→0) (Σ_(n=1) ^∞ nx^(n−1) ) lim_(x→0) (1+2x+3x^2 +4x^3 +...) 1+2x+3x^2 +4x^3 +...=S_∞ x+2x^2 +3x^3 +4x...=xS_∞ S_∞ −xS_∞ =1+x+x^2 +...=(1/(1−x)) S_∞ =(1/((1−x)^2 )) lim_(x→0) ((1/((1−x)^2 )))=1

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}} }{{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}−\mathrm{1}} \right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +…\right) \\ $$$$\:\:\:\:\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +…={S}_{\infty} \\ $$$$\:\:\:\:{x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} +\mathrm{4}{x}…={xS}_{\infty} \\ $$$$\:\:\:{S}_{\infty} −{xS}_{\infty} =\mathrm{1}+{x}+{x}^{\mathrm{2}} +…=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\:\:\:{S}_{\infty} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\right)=\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply