Question Number 183382 by mathlove last updated on 25/Dec/22
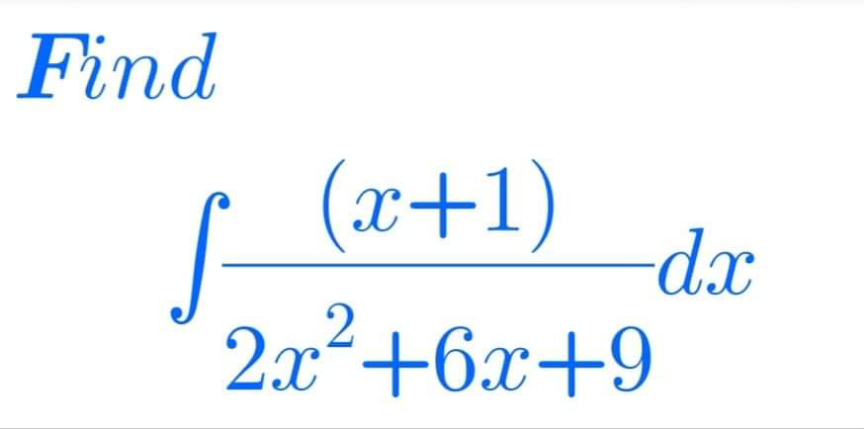
Commented by CElcedricjunior last updated on 25/Dec/22
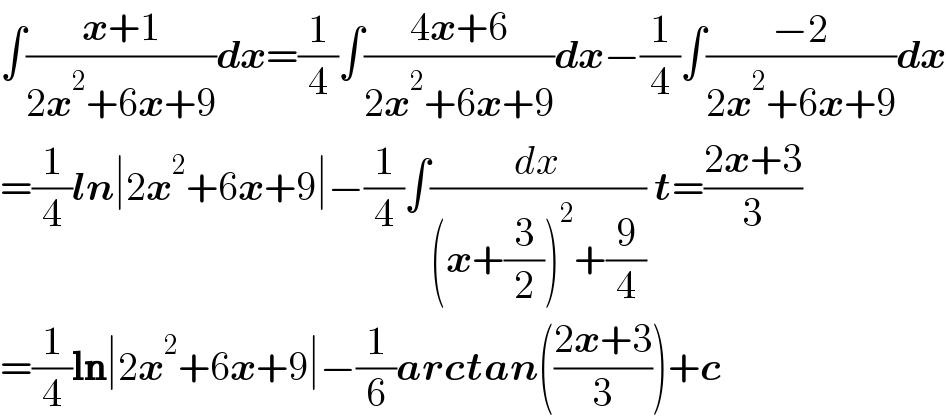
$$\int\frac{\boldsymbol{{x}}+\mathrm{1}}{\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{{x}}+\mathrm{9}}\boldsymbol{{dx}}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}\boldsymbol{{x}}+\mathrm{6}}{\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{{x}}+\mathrm{9}}\boldsymbol{{dx}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{−\mathrm{2}}{\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{{x}}+\mathrm{9}}\boldsymbol{{dx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{ln}}\mid\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{{x}}+\mathrm{9}\mid−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{\left(\boldsymbol{{x}}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}}\:\boldsymbol{{t}}=\frac{\mathrm{2}\boldsymbol{{x}}+\mathrm{3}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{\mathrm{ln}}\mid\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{{x}}+\mathrm{9}\mid−\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{{arctan}}\left(\frac{\mathrm{2}\boldsymbol{{x}}+\mathrm{3}}{\mathrm{3}}\right)+\boldsymbol{{c}} \\ $$
Commented by Acem last updated on 25/Dec/22

$$\:{Salut},\:{vous}\:{insistez}\:{pour}\:{mettre}\:{toute}\:{votre} \\ $$$$\:{solutions}\:{en}\:{commentaires}! \\ $$
Commented by mr W last updated on 26/Dec/22

$${To}\:\boldsymbol{{CElcedricjunior}}\:{sir}: \\ $$$${last}\:{warning}! \\ $$$${When}\:{you}\:{insist}\:{on}\:{disobeying}\:{the}\: \\ $$$${rules}\:{of}\:{the}\:{forum}\:{and}\:{ignore}\:{the}\: \\ $$$${kind}\:{advises}\:{of}\:{other}\:{people},\:{then}\:{this}\: \\ $$$${forum}\:{is}\:{not}\:{a}\:{suitable}\:{place}\:{for}\:{you}, \\ $$$${in}\:{other}\:{words},\:{you}\:{are}\:{not}\:{welcome} \\ $$$${here},\:{and}\:{I}'{ll}\:{ask}\:{the}\:{administrator}\: \\ $$$${to}\:{ban}\:{you}\:{from}\:{the}\:{forum}! \\ $$$${Image}\:{you}\:{are}\:{waiting}\:{for}\:{the}\:{bus} \\ $$$${at}\:{a}\:{bus}\:{stop}\:{in}\:{a}\:{queue},\:{then}\:{a}\:{guy}\: \\ $$$${comes}\:{and}\:{pushes}\:{himself}\:{before}\:{all} \\ $$$${other}\:{people}\:{in}\:{the}\:{queue}.\:{Your} \\ $$$${current}\:{behavior}\:{is}\:{exactly}\:{the}\:{same} \\ $$$${as}\:{this}\:{guy}.\:{So}\:{please}\:{leave}\:{here}\:{or} \\ $$$${obey}\:{the}\:{rules}\:{here}! \\ $$$${if}\:{you}\:{have}\:{special}\:{reason}\:{for}\:{your} \\ $$$${doing},\:{please}\:{let}\:{us}\:{know}\:{and}\:{speak} \\ $$$${it}\:{out}\:\left({in}\:{French}\:{when}\:{you}\:{like}\right).\:{Just} \\ $$$${ignoring}\:{other}\:{people}\:{without}\:{saying} \\ $$$${any}\:{thing}\:{is}\:{not}\:{polite}. \\ $$
Commented by CElcedricjunior last updated on 26/Dec/22

$${i}'{m}\:{very}\:{sor} \\ $$
Answered by Acem last updated on 25/Dec/22
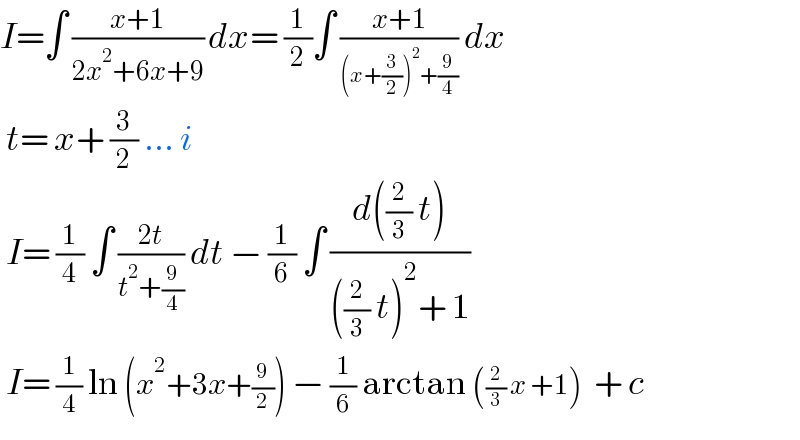
$${I}=\int\:\frac{{x}+\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9}}\:{dx}=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{x}+\mathrm{1}}{\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}}\:{dx} \\ $$$$\:{t}=\:{x}+\:\frac{\mathrm{3}}{\mathrm{2}}\:…\:{i} \\ $$$$\:{I}=\:\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}}\:{dt}\:−\:\frac{\mathrm{1}}{\mathrm{6}}\:\int\:\frac{{d}\left(\frac{\mathrm{2}}{\mathrm{3}}\:{t}\right)}{\left(\frac{\mathrm{2}}{\mathrm{3}}\:{t}\right)^{\mathrm{2}} +\:\mathrm{1}} \\ $$$$\:{I}=\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\frac{\mathrm{9}}{\mathrm{2}}\right)\:−\:\frac{\mathrm{1}}{\mathrm{6}}\:\mathrm{arctan}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\:{x}\:+\mathrm{1}\right)\:\:+\:{c} \\ $$$$ \\ $$
Answered by Tony6400 last updated on 25/Dec/22
![I=∫(x/(2x^2 +6x+9))dx+∫(1/(2x^2 +6x+9))dx=A+B Now A=∫(x/(2x^2 +6x+9))dx=∫(x/(2(x^2 +3x+(9/2))))dx=(1/2)∫(x/(x^2 +3x+((3/2))^2 +(9/2)−((3/2))^2 ))dx ⇒A=(1/2)∫(x/((x+(3/2))^2 +((3/2))^2 ))dx.Let x+(3/2)=(3/2)tanθ∴x=(3/2)(tanθ−1) ⇒(dx/dθ)=(3/2)sec^2 θ∴dx=(3/2)sec^2 θdθ ⇒A=(1/2)∫(((3/2)(tanθ−1))/(((3/2)tanθ)^2 +(9/4))).(3/2)sec^2 θdθ ∴A=(1/2)∫(((9/4)sec^2 θ(tanθ−1)dθ)/((9/4)(tan^2 θ+1)))=(1/2)∫(tanθ−1)dθ=(1/2)[−ln(cosθ)−θ].From x+(3/2)=(3/2)tanθ⇒tanθ=((2x+3)/3)=1+(2/3)x∴cosθ=(3/( (√((2x+3)^2 +9)))) And θ=arctan(1+(2/3)x)∴A=−(1/2)[ln((3/( (√((2x+3)^2 +9))))+arctan((2/3)x+1)]+C_1 Moreover B=∫(1/(2x^2 +6x+9))dx=(1/2)∫(1/((x+(3/2))^2 +((3/2))^2 ))dx=(1/2).(2/3)arctan(1+(2/3)x)+C_2 ⇒B=((arctan(1+(2/3)x))/3)+C_2 ⇒I=A+B=∫((x+1)/(2x^2 +6x+9))dx=−(1/2)[ln((3/( (√((2x+3)^2 +9)))))+arctan((2/3)x+1)]+((arctan(1+(2/3)x))/3)+K,where K=C_1 +C_2 I=−(1/2)ln((3/( (√((2x+3)^2 +9)))))−((arctan((2/3)x+1))/2)+((arctan(1+(2/3)x))/3)+K=−(1/2)ln((3/( (√((2x+3)^2 +9)))))−((arctan((2/3)x+1))/6)](https://www.tinkutara.com/question/Q183398.png)
$${I}=\int\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9}}{dx}+\int\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9}}{dx}={A}+{B} \\ $$$${Now}\:{A}=\int\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9}}{dx}=\int\frac{{x}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\frac{\mathrm{9}}{\mathrm{2}}\right)}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{3}{x}+\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{2}}−\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow{A}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}}{\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}.{Let}\:{x}+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}{tan}\theta\therefore{x}=\frac{\mathrm{3}}{\mathrm{2}}\left({tan}\theta−\mathrm{1}\right) \\ $$$$\Rightarrow\frac{{dx}}{{d}\theta}=\frac{\mathrm{3}}{\mathrm{2}}{sec}^{\mathrm{2}} \theta\therefore{dx}=\frac{\mathrm{3}}{\mathrm{2}}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$\Rightarrow{A}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{3}}{\mathrm{2}}\left({tan}\theta−\mathrm{1}\right)}{\left(\frac{\mathrm{3}}{\mathrm{2}}{tan}\theta\right)^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}}.\frac{\mathrm{3}}{\mathrm{2}}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$\therefore{A}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{9}}{\mathrm{4}}{sec}^{\mathrm{2}} \theta\left({tan}\theta−\mathrm{1}\right){d}\theta}{\frac{\mathrm{9}}{\mathrm{4}}\left({tan}^{\mathrm{2}} \theta+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int\left({tan}\theta−\mathrm{1}\right){d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\left[−{ln}\left({cos}\theta\right)−\theta\right].{From}\:{x}+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}{tan}\theta\Rightarrow{tan}\theta=\frac{\mathrm{2}{x}+\mathrm{3}}{\mathrm{3}}=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}{x}\therefore{cos}\theta=\frac{\mathrm{3}}{\:\sqrt{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}}} \\ $$$${And}\:\theta={arctan}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}{x}\right)\therefore{A}=−\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left(\frac{\mathrm{3}}{\:\sqrt{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}}}+{arctan}\left(\frac{\mathrm{2}}{\mathrm{3}}{x}+\mathrm{1}\right)\right]+{C}_{\mathrm{1}} \right. \\ $$$${Moreover}\:{B}=\int\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{3}}{arctan}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}{x}\right)+{C}_{\mathrm{2}} \\ $$$$\Rightarrow{B}=\frac{{arctan}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}{x}\right)}{\mathrm{3}}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow{I}={A}+{B}=\int\frac{{x}+\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9}}{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left(\frac{\mathrm{3}}{\:\sqrt{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}}}\right)+{arctan}\left(\frac{\mathrm{2}}{\mathrm{3}}{x}+\mathrm{1}\right)\right]+\frac{{arctan}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}{x}\right)}{\mathrm{3}}+{K},{where}\:{K}={C}_{\mathrm{1}} +{C}_{\mathrm{2}} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}}{\:\sqrt{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}}}\right)−\frac{{arctan}\left(\frac{\mathrm{2}}{\mathrm{3}}{x}+\mathrm{1}\right)}{\mathrm{2}}+\frac{{arctan}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}{x}\right)}{\mathrm{3}}+{K}=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}}{\:\sqrt{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}}}\right)−\frac{{arctan}\left(\frac{\mathrm{2}}{\mathrm{3}}{x}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
