Question Number 183393 by cherokeesay last updated on 25/Dec/22

Answered by mr W last updated on 25/Dec/22
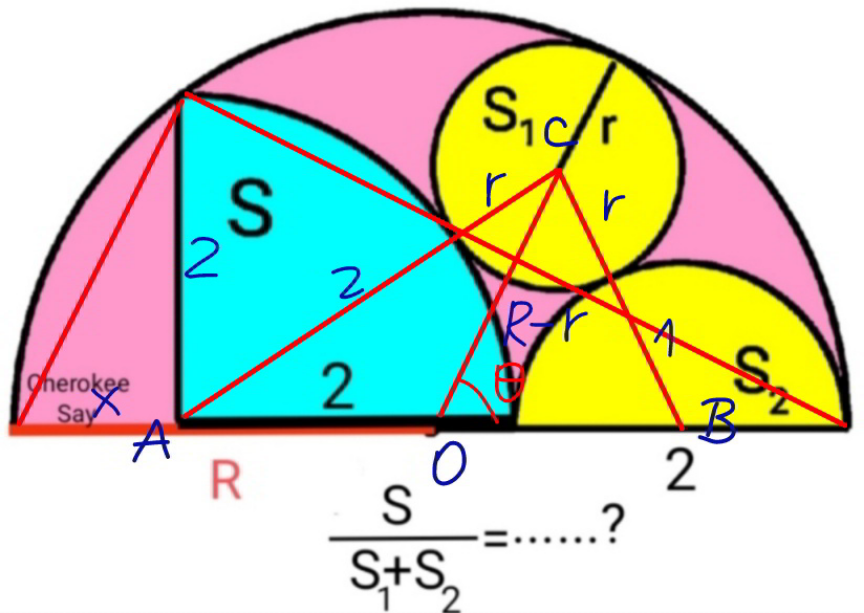
Commented by mr W last updated on 25/Dec/22

$$\frac{{x}}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{2}+\mathrm{2}} \\ $$$$\Rightarrow{x}=\mathrm{1} \\ $$$${R}=\frac{\mathrm{1}+\mathrm{2}+\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\theta=\frac{\left({R}−{r}\right)^{\mathrm{2}} +\left({R}−\mathrm{1}\right)^{\mathrm{2}} −\left({r}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}−{r}\right)\left({R}−\mathrm{1}\right)} \\ $$$$\mathrm{cos}\:\theta=\frac{\left({r}+\mathrm{2}\right)^{\mathrm{2}} −\left({R}−\mathrm{1}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}−{r}\right)\left({R}−\mathrm{1}\right)} \\ $$$$\left({r}+\mathrm{2}\right)^{\mathrm{2}} −\left({R}−\mathrm{1}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} =\left({R}−{r}\right)^{\mathrm{2}} +\left({R}−\mathrm{1}\right)^{\mathrm{2}} −\left({r}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{9}\left({r}−\frac{\mathrm{1}}{\mathrm{4}}\right)−\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{7}\left(\frac{\mathrm{3}}{\mathrm{4}}−{r}\right)+\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${S}=\frac{\pi×\mathrm{2}^{\mathrm{2}} }{\mathrm{4}}=\pi \\ $$$${S}_{\mathrm{1}} =\pi{r}^{\mathrm{2}} \\ $$$${S}_{\mathrm{2}} =\frac{\pi×\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}=\frac{\pi}{\mathrm{2}} \\ $$$$\frac{{S}}{{S}_{\mathrm{1}} +{S}_{\mathrm{2}} }=\frac{\pi}{\pi{r}^{\mathrm{2}} +\frac{\pi}{\mathrm{2}}}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{2}{r}^{\mathrm{2}} }=\frac{\mathrm{16}}{\mathrm{17}}\:\checkmark \\ $$
Commented by mr W last updated on 25/Dec/22
$${error}\:{is}\:{fixed}.\:{thanks}! \\ $$
Commented by cherokeesay last updated on 25/Dec/22

$${c}'{est}\:\frac{\mathrm{16}}{\mathrm{17}},\:{il}\:{y}\:{a}\:{erreur}\:{dans}\:{vos}\:{calculs}\:{sir}. \\ $$
Answered by Acem last updated on 25/Dec/22

Commented by Acem last updated on 27/Dec/22

$$\:{BD}\:{is}\:{a}\:{half}\:{of}\:{the}\:{chord}\:{so}\:\mid{BD}\mid^{\mathrm{2}} =\:\mid{AD}\mid.\:\mid{DC}\mid \\ $$
Commented by Acem last updated on 25/Dec/22

$$\:{Continue}… \\ $$
Commented by Acem last updated on 26/Dec/22

Commented by Acem last updated on 27/Dec/22

Answered by HeferH last updated on 25/Dec/22

Commented by cherokeesay last updated on 25/Dec/22

$${il}\:{y}\:{a}\:{erreur}\:{dans}\:{vos}\:{calculs}\:! \\ $$$${c}'{est}\:\frac{\mathrm{16}}{\mathrm{17}} \\ $$
