Question Number 183524 by aurpeyz last updated on 26/Dec/22

Answered by mr W last updated on 26/Dec/22
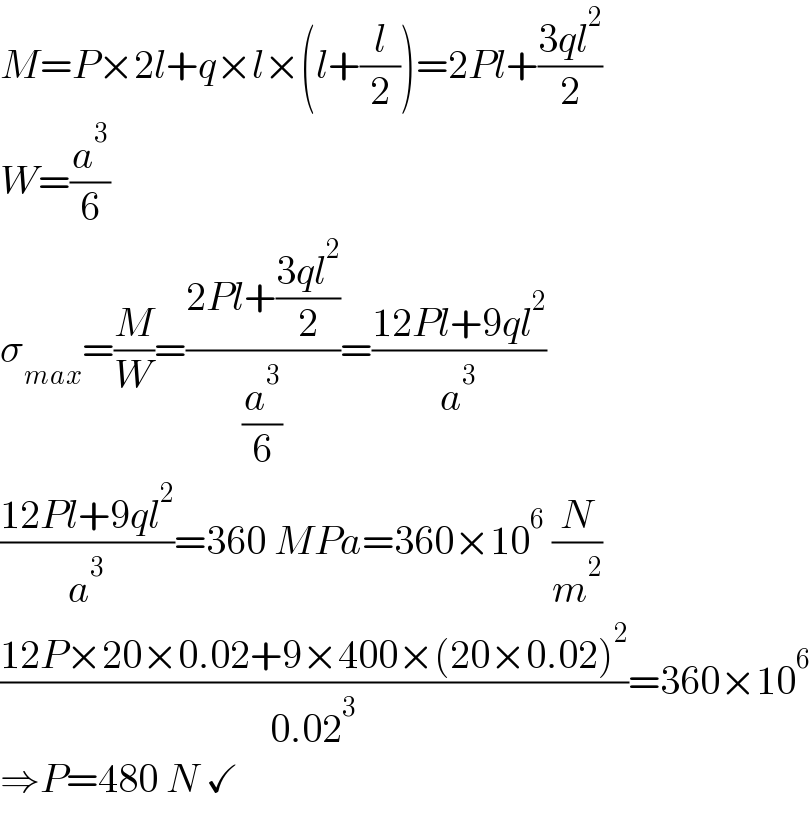
$${M}={P}×\mathrm{2}{l}+{q}×{l}×\left({l}+\frac{{l}}{\mathrm{2}}\right)=\mathrm{2}{Pl}+\frac{\mathrm{3}{ql}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${W}=\frac{{a}^{\mathrm{3}} }{\mathrm{6}} \\ $$$$\sigma_{{max}} =\frac{{M}}{{W}}=\frac{\mathrm{2}{Pl}+\frac{\mathrm{3}{ql}^{\mathrm{2}} }{\mathrm{2}}}{\frac{{a}^{\mathrm{3}} }{\mathrm{6}}}=\frac{\mathrm{12}{Pl}+\mathrm{9}{ql}^{\mathrm{2}} }{{a}^{\mathrm{3}} } \\ $$$$\frac{\mathrm{12}{Pl}+\mathrm{9}{ql}^{\mathrm{2}} }{{a}^{\mathrm{3}} }=\mathrm{360}\:{MPa}=\mathrm{360}×\mathrm{10}^{\mathrm{6}} \:\frac{{N}}{{m}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{12}{P}×\mathrm{20}×\mathrm{0}.\mathrm{02}+\mathrm{9}×\mathrm{400}×\left(\mathrm{20}×\mathrm{0}.\mathrm{02}\right)^{\mathrm{2}} }{\mathrm{0}.\mathrm{02}^{\mathrm{3}} }=\mathrm{360}×\mathrm{10}^{\mathrm{6}} \\ $$$$\Rightarrow{P}=\mathrm{480}\:{N}\:\checkmark \\ $$
Commented by aurpeyz last updated on 27/Dec/22

$${thanks} \\ $$
