Question Number 183533 by MikeH last updated on 26/Dec/22
Commented by MikeH last updated on 26/Dec/22

$$\mathrm{please}\:\mathrm{guys}\:\mathrm{solve}\:\mathrm{using}\:\mathrm{the}\:\mathrm{method}\:\mathrm{undetermined} \\ $$$$\mathrm{coefficients}\:\mathrm{or}\:\mathrm{variation}\:\mathrm{of}\:\mathrm{parameters}. \\ $$
Answered by qaz last updated on 27/Dec/22
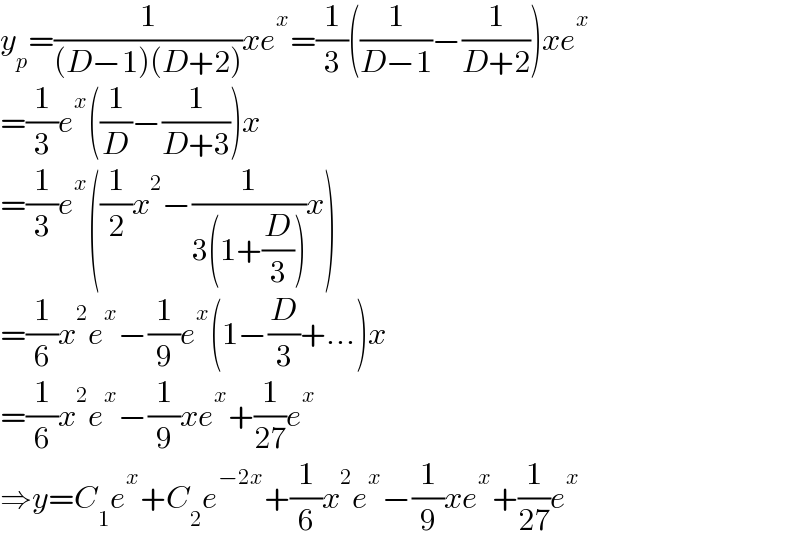
$${y}_{{p}} =\frac{\mathrm{1}}{\left({D}−\mathrm{1}\right)\left({D}+\mathrm{2}\right)}{xe}^{{x}} =\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{{D}−\mathrm{1}}−\frac{\mathrm{1}}{{D}+\mathrm{2}}\right){xe}^{{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{{x}} \left(\frac{\mathrm{1}}{{D}}−\frac{\mathrm{1}}{{D}+\mathrm{3}}\right){x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{{x}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+\frac{{D}}{\mathrm{3}}\right)}{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{2}} {e}^{{x}} −\frac{\mathrm{1}}{\mathrm{9}}{e}^{{x}} \left(\mathrm{1}−\frac{{D}}{\mathrm{3}}+…\right){x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{2}} {e}^{{x}} −\frac{\mathrm{1}}{\mathrm{9}}{xe}^{{x}} +\frac{\mathrm{1}}{\mathrm{27}}{e}^{{x}} \\ $$$$\Rightarrow{y}={C}_{\mathrm{1}} {e}^{{x}} +{C}_{\mathrm{2}} {e}^{−\mathrm{2}{x}} +\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{2}} {e}^{{x}} −\frac{\mathrm{1}}{\mathrm{9}}{xe}^{{x}} +\frac{\mathrm{1}}{\mathrm{27}}{e}^{{x}} \\ $$
Answered by FelipeLz last updated on 26/Dec/22
![y′′+y′−2y = 0 y = e^r → r^2 e^r +re^r −2e^r = 0 r^2 +r−2 = 0 → r = { (1),((−2)) :} y_h (x) = c_1 y_1 (x)+c_2 y_2 (x) = c_1 e^x +c_2 e^(−2x) y_p (x) = u(x)y_1 (x)+v(x)y_2 (x) y_p (x) = u(x)e^x +v(x)e^(−2x) { ((u′(x)e^x +v′(x)e^(−2x) = 0)),((u′(x)e^x +v′(x)(−2e^(−2x) ) = xe^x )) :} u′(x) = ( determinant ((( 0),( e^(−2x) )),((xe^x ),(−2e^(−2x) )))/ determinant ((e^x ,e^(−2x) ),(e^x ,(−2e^(−2x) )))) = ((−xe^(−x) )/(−2e^(−x) −e^(−x) )) = (x/3) u(x) = (1/3)∫xdx = (x^2 /6) v′(x) = ( determinant ((e^x ,0),(e^x ,(xe^x )))/ determinant ((e^x ,e^(−2x) ),(e^x ,(−2e^(−2x) )))) = ((xe^(2x) )/(−2e^(−x) −e^(−x) )) = −((xe^(3x) )/3) v(x) = −(1/3)∫xe^(3x) dx = −(1/3)[(1/3)xe^(3x) −(1/3)∫e^(3x) dx] = −(1/9)xe^(3x) +(1/(27))e^(3x) y_p (x) = (x^2 /6)e^x +(−(x/9)e^(3x) +(1/(27))e^(3x) )e^(−2x) y_p (x) = (x^2 /6)e^x −(x/9)e^x +(1/(27))e^x y(x) = y_h (x)+y_p (x) y(x) = ((x^2 /6)−(x/9)+(1/(27))+c_1 )e^x +c_2 e^(−2x) o](https://www.tinkutara.com/question/Q183537.png)
$${y}''+{y}'−\mathrm{2}{y}\:=\:\mathrm{0} \\ $$$${y}\:=\:{e}^{{r}} \:\rightarrow\:{r}^{\mathrm{2}} {e}^{{r}} +{re}^{{r}} −\mathrm{2}{e}^{{r}} \:=\:\mathrm{0} \\ $$$${r}^{\mathrm{2}} +{r}−\mathrm{2}\:=\:\mathrm{0}\:\rightarrow\:{r}\:=\:\begin{cases}{\mathrm{1}}\\{−\mathrm{2}}\end{cases}\: \\ $$$${y}_{{h}} \left({x}\right)\:=\:{c}_{\mathrm{1}} {y}_{\mathrm{1}} \left({x}\right)+{c}_{\mathrm{2}} {y}_{\mathrm{2}} \left({x}\right)\:=\:{c}_{\mathrm{1}} {e}^{{x}} +{c}_{\mathrm{2}} {e}^{−\mathrm{2}{x}} \\ $$$$\: \\ $$$${y}_{{p}} \left({x}\right)\:=\:{u}\left({x}\right){y}_{\mathrm{1}} \left({x}\right)+{v}\left({x}\right){y}_{\mathrm{2}} \left({x}\right) \\ $$$${y}_{{p}} \left({x}\right)\:=\:{u}\left({x}\right){e}^{{x}} +{v}\left({x}\right){e}^{−\mathrm{2}{x}} \\ $$$$\begin{cases}{{u}'\left({x}\right){e}^{{x}} +{v}'\left({x}\right){e}^{−\mathrm{2}{x}} \:=\:\mathrm{0}}\\{{u}'\left({x}\right){e}^{{x}} +{v}'\left({x}\right)\left(−\mathrm{2}{e}^{−\mathrm{2}{x}} \right)\:=\:{xe}^{{x}} }\end{cases} \\ $$$${u}'\left({x}\right)\:=\:\frac{\begin{vmatrix}{\:\:\mathrm{0}}&{\:\:\:\:{e}^{−\mathrm{2}{x}} }\\{{xe}^{{x}} }&{−\mathrm{2}{e}^{−\mathrm{2}{x}} }\end{vmatrix}}{\begin{vmatrix}{{e}^{{x}} }&{{e}^{−\mathrm{2}{x}} }\\{{e}^{{x}} }&{−\mathrm{2}{e}^{−\mathrm{2}{x}} }\end{vmatrix}}\:=\:\frac{−{xe}^{−{x}} }{−\mathrm{2}{e}^{−{x}} −{e}^{−{x}} }\:=\:\frac{{x}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{u}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int{xdx}\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{6}} \\ $$$${v}'\left({x}\right)\:=\:\frac{\begin{vmatrix}{{e}^{{x}} }&{\mathrm{0}}\\{{e}^{{x}} }&{{xe}^{{x}} }\end{vmatrix}}{\begin{vmatrix}{{e}^{{x}} }&{{e}^{−\mathrm{2}{x}} }\\{{e}^{{x}} }&{−\mathrm{2}{e}^{−\mathrm{2}{x}} }\end{vmatrix}}\:=\:\frac{{xe}^{\mathrm{2}{x}} }{−\mathrm{2}{e}^{−{x}} −{e}^{−{x}} }\:=\:−\frac{{xe}^{\mathrm{3}{x}} }{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{v}\left({x}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\int{xe}^{\mathrm{3}{x}} {dx}\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{1}}{\mathrm{3}}{xe}^{\mathrm{3}{x}} −\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{\mathrm{3}{x}} {dx}\right]\:=\:−\frac{\mathrm{1}}{\mathrm{9}}{xe}^{\mathrm{3}{x}} +\frac{\mathrm{1}}{\mathrm{27}}{e}^{\mathrm{3}{x}} \\ $$$${y}_{{p}} \left({x}\right)\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{6}}{e}^{{x}} +\left(−\frac{{x}}{\mathrm{9}}{e}^{\mathrm{3}{x}} +\frac{\mathrm{1}}{\mathrm{27}}{e}^{\mathrm{3}{x}} \right){e}^{−\mathrm{2}{x}} \\ $$$${y}_{{p}} \left({x}\right)\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{6}}{e}^{{x}} −\frac{{x}}{\mathrm{9}}{e}^{{x}} +\frac{\mathrm{1}}{\mathrm{27}}{e}^{{x}} \\ $$$$\: \\ $$$${y}\left({x}\right)\:=\:{y}_{{h}} \left({x}\right)+{y}_{{p}} \left({x}\right) \\ $$$${y}\left({x}\right)\:=\:\left(\frac{{x}^{\mathrm{2}} }{\mathrm{6}}−\frac{{x}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{27}}+{c}_{\mathrm{1}} \right){e}^{{x}} +{c}_{\mathrm{2}} {e}^{−\mathrm{2}{x}} {o} \\ $$
Commented by MikeH last updated on 26/Dec/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
