Question Number 183558 by Acem last updated on 27/Dec/22

Commented by Acem last updated on 27/Dec/22

$$\:{The}\:{inlet}\:{segment}\:\bot\:{Hypotenuse} \\ $$
Answered by HeferH last updated on 27/Dec/22

$$\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{2}}{\mathrm{5}}\:=\:\frac{\mathrm{3}}{\mathrm{5}}\:=\:\frac{\mathrm{3}{k}}{\mathrm{5}{k}}\: \\ $$$$\:{A}=\mathrm{8}{k}\: \\ $$$$\: \\ $$
Commented by Acem last updated on 27/Dec/22

$${Hi}\:{Sir}! \\ $$$$\:{why}\:\frac{\mathrm{2}}{\mathrm{5}}? \\ $$
Commented by HeferH last updated on 27/Dec/22

$$\frac{\frac{\mathrm{3}}{\mathrm{2}}}{\frac{\mathrm{5}}{\mathrm{2}}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{2}}{\mathrm{5}}\: \\ $$
Commented by Acem last updated on 27/Dec/22
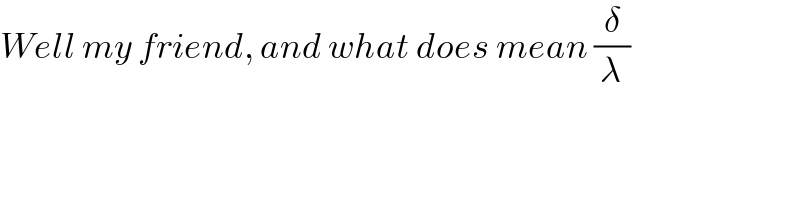
$${Well}\:{my}\:{friend},\:{and}\:{what}\:{does}\:{mean}\:\frac{\delta}{\lambda} \\ $$
Commented by HeferH last updated on 27/Dec/22

$${When}\:{you}\:{have}\:{a}\:{line}\:{that}\:{goes}\:{from}\:{one}\:{vertex} \\ $$$$\:{to}\:{any}\:{point}\:{of}\:{the}\:{oposite}\:{side}\:\left({triangle}\right) \\ $$$$\:{the}\:{ratio}\:{of}\:{the}\:{bases}\:{is}\:{equal}\:{to}\:{the}\:{ratio}\:{of} \\ $$$$\:{their}\:{areas} \\ $$$$\:\frac{{a}}{{b}}\:=\:\frac{{A}_{\mathrm{1}} }{{A}_{\mathrm{2}} }\:\:{or}\:\frac{{A}_{\mathrm{2}} }{{b}}\:=\:\frac{{A}_{\mathrm{1}} }{{a}} \\ $$$$\:{One}\:{interpretation}\:{is}\:{that}\:{the}\:{base}\: \\ $$$$\:{is}\:{proportional}\:{to}\:{the}\:{area} \\ $$$$\:\left({if}\:{the}\:{height}\:{is}\:{fixed}\right) \\ $$$$\: \\ $$
Commented by Acem last updated on 27/Dec/22
, 4[](https://www.tinkutara.com/question/Q183566.png)
$${Very}\:{good},\:{thank}\:{you}!\:{so}\:{how}\:{it}\:{helps}\:{to}\:{find}\:{the} \\ $$$$\:{entire}\:{area}\:{of}\:{that}\:{triangle}? \\ $$$$\:{The}\:{inlet}\:{segment}\:\bot\:{Hypotenuse} \\ $$$$\left.\:{Knowing}\:{that}\:{its}\:{area}\:\in\:\right]\frac{\mathrm{5}}{\mathrm{2}},\:\mathrm{4}\left[\right. \\ $$
Commented by HeferH last updated on 27/Dec/22
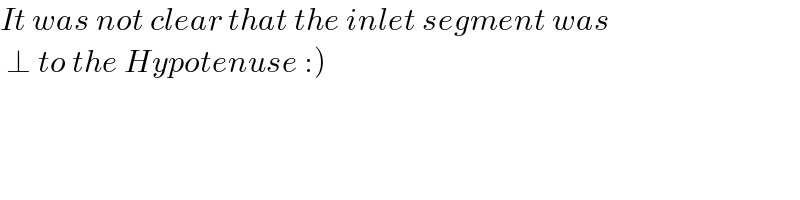
$${It}\:{was}\:{not}\:{clear}\:{that}\:{the}\:{inlet}\:{segment}\:{was} \\ $$$$\left.\:\bot\:{to}\:{the}\:{Hypotenuse}\::\right) \\ $$
Commented by Acem last updated on 27/Dec/22
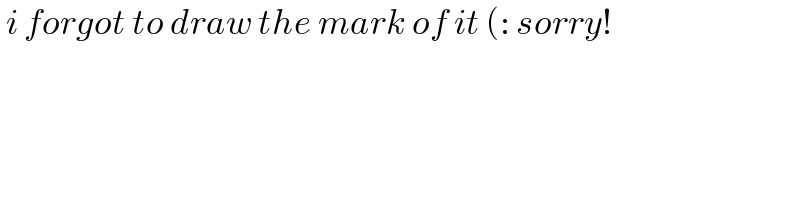
$$\:{i}\:{forgot}\:{to}\:{draw}\:{the}\:{mark}\:{of}\:{it}\:\left(:\:{sorry}!\right. \\ $$
Answered by HeferH last updated on 27/Dec/22
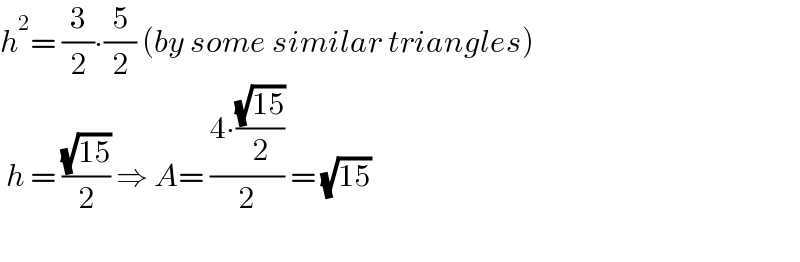
$${h}^{\mathrm{2}} =\:\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{5}}{\mathrm{2}}\:\left({by}\:{some}\:{similar}\:{triangles}\right) \\ $$$$\:{h}\:=\:\frac{\sqrt{\mathrm{15}}}{\mathrm{2}}\:\Rightarrow\:{A}=\:\frac{\mathrm{4}\centerdot\frac{\sqrt{\mathrm{15}}}{\mathrm{2}}}{\mathrm{2}}\:=\:\sqrt{\mathrm{15}} \\ $$$$\: \\ $$
Commented by Acem last updated on 27/Dec/22

$${Thankkkk}\:{you}\:{Sir}!\:\left(:\right. \\ $$
Answered by Acem last updated on 27/Dec/22

Commented by Acem last updated on 27/Dec/22

$$\:{We}\:{must}\:{notforget}\:{the}\:{story}\:{of}\:{the}\:{chord}\:{of}\:{the} \\ $$$$\:{circle}\:{passing}\:{through}\:{the}\:{vertices}\:{of}\:{the}\:{triangle} \\ $$$$\:\:\omega^{\mathrm{2}} =\:{m}.{n}\:\left\{\:\mathrm{2}\:{segments}\:{of}\:{the}\:{diameter}\right\} \\ $$$$\:{That}\:{if}\:{didn}'{t}\:{mind}\:{the}\:{story}\:{of}\:{similar}\:{triangles} \\ $$
Commented by HeferH last updated on 27/Dec/22

$${Yeah},\:{I}\:{realize}\:{that}\:{many}\:{times}\:{when}\:{I}\:{had} \\ $$$$\:{a}\:{rect}\:{triangle}\:{inside}\:{a}\:{circunference}\:{while}\: \\ $$$${working}\:{on}\:{other}\:{problems}. \\ $$$$\:{I}\:{tought}\:{it}\:{was}\:{a}\:{coincidence}\:{but}\:{it}\:{is}\:{also} \\ $$$$\:{another}\:{way}\:{of}\:{demonstrate}\:{it}. \\ $$$$\:{Sorry}\:{if}\:{I}\:{sound}\:{a}\:{bit}\:{weird}\:{sometimes},\: \\ $$$$\:{english}\:{its}\:{not}\:{my}\:{first}\:{language}\::/ \\ $$
