Question Number 183663 by AROUNAMoussa last updated on 28/Dec/22
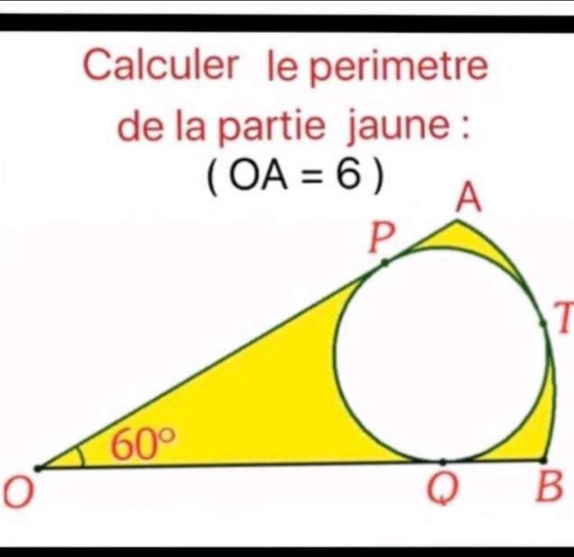
Commented by mathocean1 last updated on 28/Dec/22

$${Perimetre}=\mathrm{2}\pi+\mathrm{12} \\ $$
Answered by a.lgnaoui last updated on 28/Dec/22

$${P}={P}_{\mathrm{1}} +{P}_{\mathrm{2}} +{P}\mathrm{3} \\ $$$${P}_{\mathrm{1}} ={perumetre}\left({OPQ}\right) \\ $$$${P}_{\mathrm{2}} ={perimetre}\left({QBR}\right) \\ $$$${P}_{\mathrm{3}} ={perimetre}\left({RAP}\right) \\ $$$${P}_{\mathrm{4}} ={perimetre}\left({OABO}\right) \\ $$$${P}=\mathrm{Arc}\left({PQ}\right)+{Arc}\left({QR}\right)+{Arc}\left({PR}\right)+{P}_{\mathrm{4}} \\ $$$${P}=\mathrm{2}\pi{r}+\mathrm{12}+\mathrm{2}\pi\:\:\left({r}={rayn}\:{du}\:{cercle}\:{inscrit}\right) \\ $$$$\mathrm{sin}\:\:\mathrm{30}=\frac{{r}}{{OO}_{\mathrm{1}} }=\frac{{r}}{\mathrm{6}−{r}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{2}{r}=\mathrm{6}\sqrt{\mathrm{3}}\:−{r}\sqrt{\mathrm{3}}\:\Rightarrow{r}=\frac{\mathrm{6}\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$${perimetre}\:{du}\:{cercle}=\mathrm{2}\pi{r}=\frac{\mathrm{12}\pi\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$${P}=\mathrm{2}\pi{r}+\left(\mathrm{2}\pi+\mathrm{12}\right) \\ $$$$\:\:\:\:\:=\mathrm{12}+\mathrm{2}\pi\left(\mathrm{12}\sqrt{\mathrm{3}}\:−\mathrm{17}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{P}=\mathrm{35},\mathrm{7794} \\ $$
Commented by a.lgnaoui last updated on 28/Dec/22
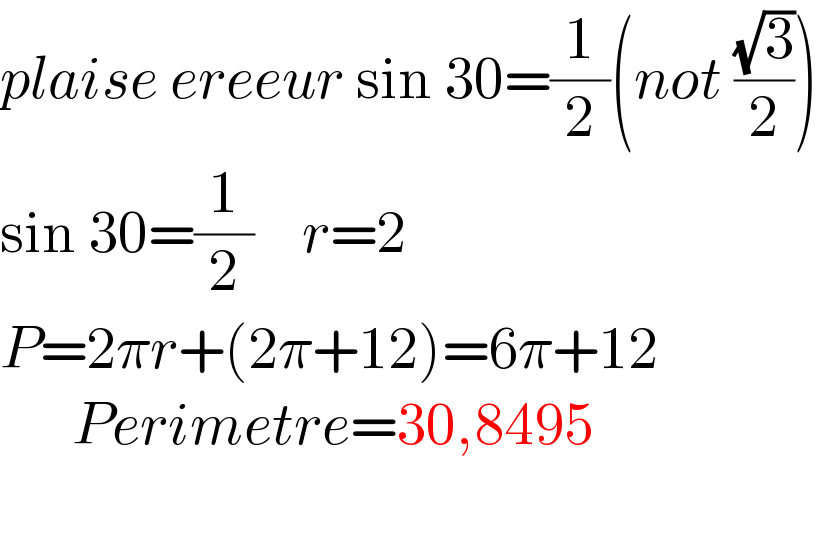
$${plaise}\:{ereeur}\:\mathrm{sin}\:\mathrm{30}=\frac{\mathrm{1}}{\mathrm{2}}\left({not}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\mathrm{sin}\:\mathrm{30}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:{r}=\mathrm{2}\:\:\: \\ $$$${P}=\mathrm{2}\pi{r}+\left(\mathrm{2}\pi+\mathrm{12}\right)=\mathrm{6}\pi+\mathrm{12} \\ $$$$\:\:\:\:\:\:{Perimetre}=\mathrm{30},\mathrm{8495} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 28/Dec/22
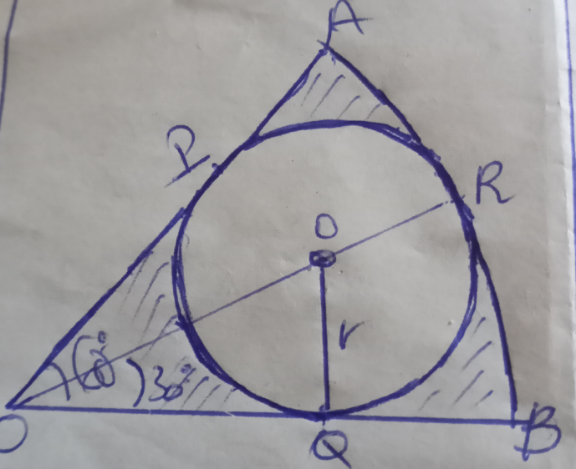
Answered by manxsol last updated on 28/Dec/22
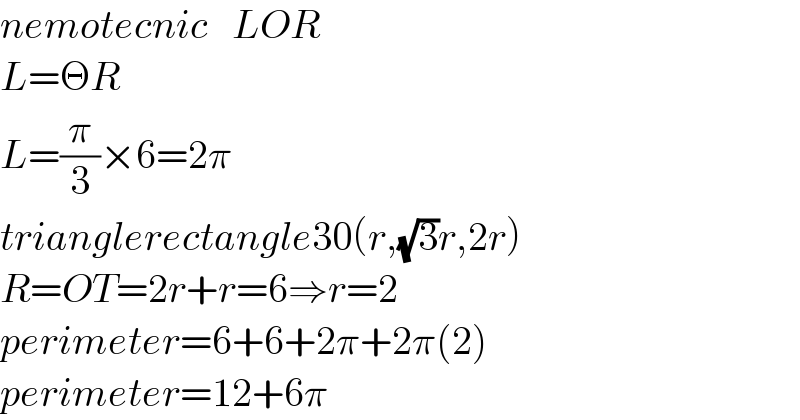
$${nemotecnic}\:\:\:{LOR} \\ $$$${L}=\Theta{R} \\ $$$${L}=\frac{\pi}{\mathrm{3}}×\mathrm{6}=\mathrm{2}\pi \\ $$$${trianglerectangle}\mathrm{30}\left({r},\sqrt{\mathrm{3}}{r},\mathrm{2}{r}\right) \\ $$$${R}={OT}=\mathrm{2}{r}+{r}=\mathrm{6}\Rightarrow{r}=\mathrm{2} \\ $$$${perimeter}=\mathrm{6}+\mathrm{6}+\mathrm{2}\pi+\mathrm{2}\pi\left(\mathrm{2}\right) \\ $$$${perimeter}=\mathrm{12}+\mathrm{6}\pi \\ $$
