Question Number 183728 by mr W last updated on 29/Dec/22
Commented by mr W last updated on 29/Dec/22

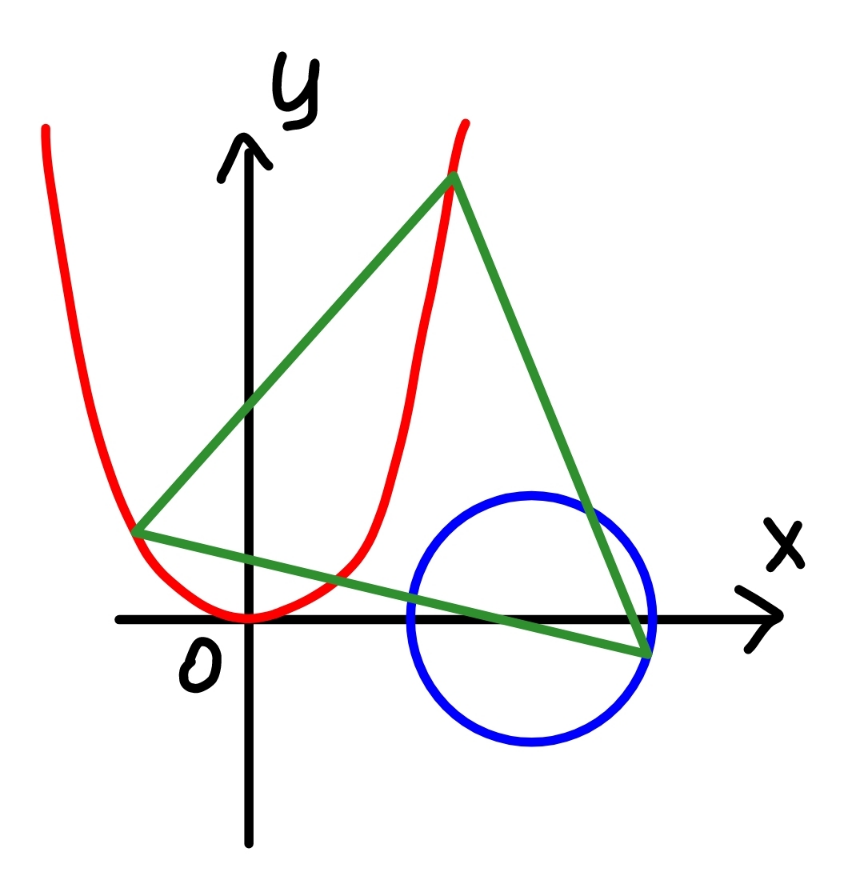
$${find}\:{the}\:{smallest}\:{and}\:{the}\:{largest} \\ $$$${equilateral}\:{triangle}\:{which}\:{has}\:{two} \\ $$$${of}\:{its}\:{vertices}\:{on}\:{the}\:{parabola}\:{y}=\mathrm{2}{x}^{\mathrm{2}} \\ $$$${and}\:{the}\:{third}\:{vertex}\:{on}\:{the}\:{circle} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}=\mathrm{0}. \\ $$
Answered by mr W last updated on 29/Dec/22
Commented by mr W last updated on 29/Dec/22
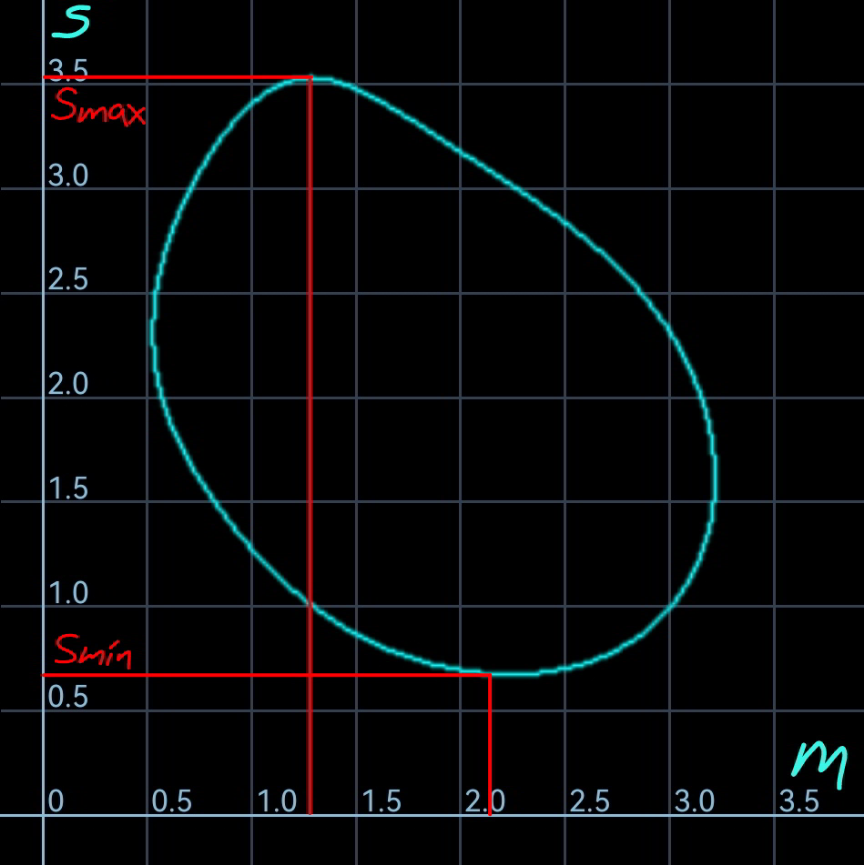
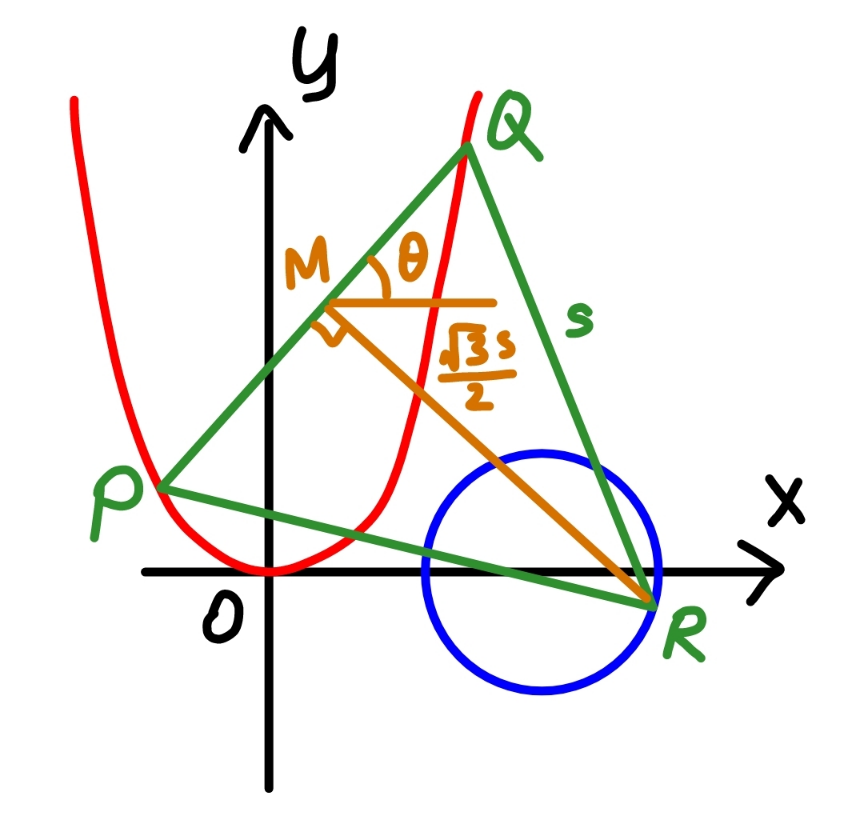
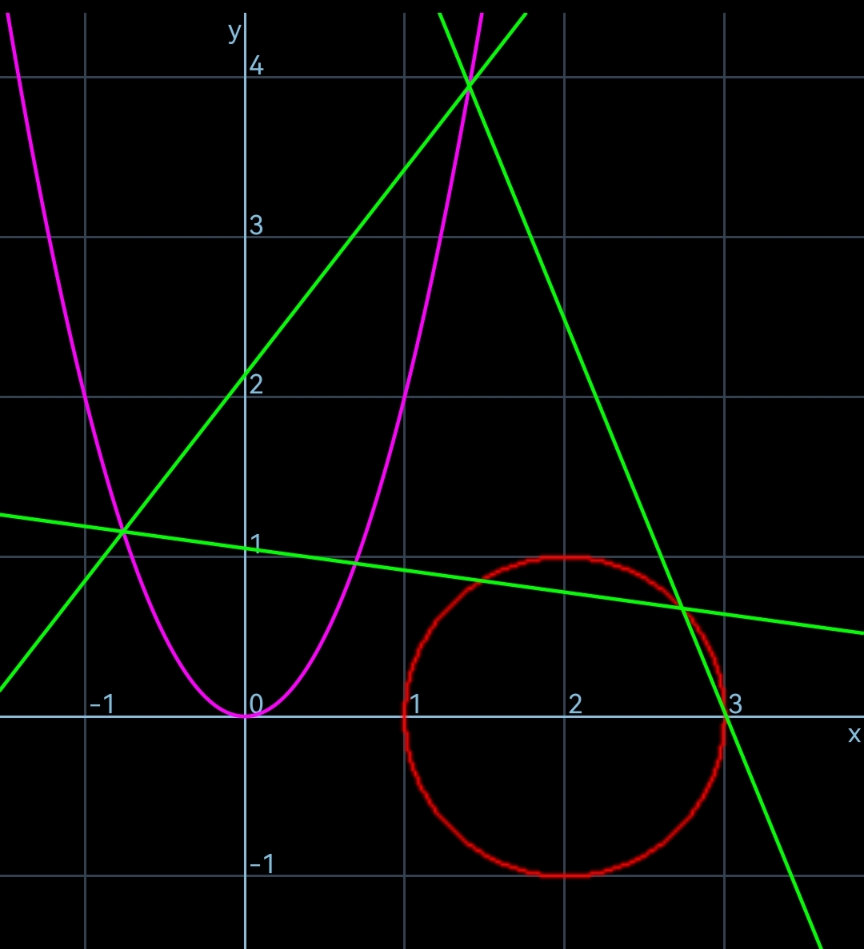
![parabola: y=2x^2 circle: (x−2)^2 +y^2 =1^2 let m=tan θ M(h,k) eqn. of PQ: y=m(x−h)+k intersection P and Q: 2x^2 =m(x−h)+k x^2 −(m/2)x+((mh−k)/2)=0 ⇒x_1 +x_2 =(m/2), x_1 x_2 =((mh−k)/2) h=((x_1 +x_2 )/2)=(m/4) (x_2 −x_1 )^2 +(y_2 −y_1 )^2 =s^2 (x_2 +x_1 )^2 −4x_1 x_2 +4(x_2 ^2 −x_1 ^2 )^2 =s^2 (x_2 +x_1 )^2 −4x_1 x_2 +4[(x_1 +x_2 )^2 −2x_1 x_2 ]^2 −4(2x_1 x_2 )^2 =s^2 4h^2 −2mh+2k+4(4h^2 −mh+k)^2 −4(mh−k)^2 =s^2 −4h^2 +2k+4k^2 −4(4h^2 −k)^2 =s^2 ⇒k=((s^2 +64h^4 +4h^2 )/(2(16h^2 +1)))=((4s^2 +m^4 +m^2 )/(8(m^2 +1)))=(s^2 /(2(m^2 +1)))+(m^2 /8) x_R =h+(((√3)s)/2) sin θ=(m/4)+((m(√3)s)/(2(√(m^2 +1)))) y_R =k−(((√3)s)/2) cos θ=k−(((√3)s)/(2(√(m^2 +1)))) ⇒((m/4)+((m(√3)s)/(2(√(m^2 +1))))−2)^2 +((s^2 /(2(m^2 +1)))+(m^2 /8)−(((√3)s)/(2(√(m^2 +1)))))^2 =1 ⇒s_(min) ≈0.6771 at m≈2.237 ⇒s_(max) ≈3.5303 at m≈1.288](https://www.tinkutara.com/question/Q183757.png)
$${parabola}:\:{y}=\mathrm{2}{x}^{\mathrm{2}} \\ $$$${circle}:\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \\ $$$${let}\:{m}=\mathrm{tan}\:\theta \\ $$$${M}\left({h},{k}\right) \\ $$$${eqn}.\:{of}\:{PQ}: \\ $$$${y}={m}\left({x}−{h}\right)+{k} \\ $$$${intersection}\:{P}\:{and}\:{Q}: \\ $$$$\mathrm{2}{x}^{\mathrm{2}} ={m}\left({x}−{h}\right)+{k} \\ $$$${x}^{\mathrm{2}} −\frac{{m}}{\mathrm{2}}{x}+\frac{{mh}−{k}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\frac{{m}}{\mathrm{2}},\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} =\frac{{mh}−{k}}{\mathrm{2}} \\ $$$${h}=\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }{\mathrm{2}}=\frac{{m}}{\mathrm{4}} \\ $$$$\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({y}_{\mathrm{2}} −{y}_{\mathrm{1}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{2}} +{x}_{\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{1}} {x}_{\mathrm{2}} +\mathrm{4}\left({x}_{\mathrm{2}} ^{\mathrm{2}} −{x}_{\mathrm{1}} ^{\mathrm{2}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{2}} +{x}_{\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{1}} {x}_{\mathrm{2}} +\mathrm{4}\left[\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{2}} \right]^{\mathrm{2}} −\mathrm{4}\left(\mathrm{2}{x}_{\mathrm{1}} {x}_{\mathrm{2}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\mathrm{4}{h}^{\mathrm{2}} −\mathrm{2}{mh}+\mathrm{2}{k}+\mathrm{4}\left(\mathrm{4}{h}^{\mathrm{2}} −{mh}+{k}\right)^{\mathrm{2}} −\mathrm{4}\left({mh}−{k}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$−\mathrm{4}{h}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{4}{k}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{4}{h}^{\mathrm{2}} −{k}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\Rightarrow{k}=\frac{{s}^{\mathrm{2}} +\mathrm{64}{h}^{\mathrm{4}} +\mathrm{4}{h}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{16}{h}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{4}{s}^{\mathrm{2}} +{m}^{\mathrm{4}} +{m}^{\mathrm{2}} }{\mathrm{8}\left({m}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{s}^{\mathrm{2}} }{\mathrm{2}\left({m}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{{m}^{\mathrm{2}} }{\mathrm{8}} \\ $$$${x}_{{R}} ={h}+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta=\frac{{m}}{\mathrm{4}}+\frac{{m}\sqrt{\mathrm{3}}{s}}{\mathrm{2}\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${y}_{{R}} ={k}−\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\mathrm{cos}\:\theta={k}−\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\Rightarrow\left(\frac{{m}}{\mathrm{4}}+\frac{{m}\sqrt{\mathrm{3}}{s}}{\mathrm{2}\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}}−\mathrm{2}\right)^{\mathrm{2}} +\left(\frac{{s}^{\mathrm{2}} }{\mathrm{2}\left({m}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{{m}^{\mathrm{2}} }{\mathrm{8}}−\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{s}_{{min}} \approx\mathrm{0}.\mathrm{6771}\:{at}\:{m}\approx\mathrm{2}.\mathrm{237} \\ $$$$\Rightarrow{s}_{{max}} \approx\mathrm{3}.\mathrm{5303}\:{at}\:{m}\approx\mathrm{1}.\mathrm{288} \\ $$
Commented by mr W last updated on 29/Dec/22
Commented by mr W last updated on 29/Dec/22
Commented by mr W last updated on 29/Dec/22